Chapitre 4 Arbres
Nous avons déjà vu la notion de fonction récursive dans le chapitre
2. Considérons à présent son équivalent dans les
structures de données: la notion d'arbre. Un arbre
est soit un arbre atomique (une feuille), soit un noeud
et une suite de sous-arbres. Graphiquement, un arbre est représenté
comme suit
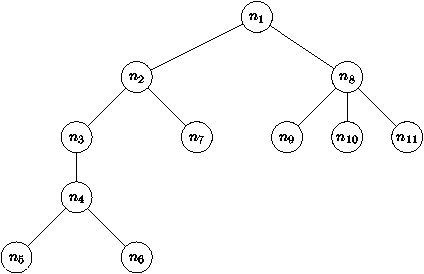
Figure 4.1 : Un exemple d'arbre
Le noeud n1 est la racine de l'arbre, n5, n6,
n7, n9, n10, n11 sont les feuilles, n1, n2,
n3, n4, n8 les noeuds internes. Plus généralement,
l'ensemble des noeuds est constitué des noeuds internes et des
feuilles. Contrairement à la botanique, on dessine les arbres avec
la racine en haut et les feuilles vers le bas en informatique. Il y a
bien des définitions plus mathématiques des arbres, que nous
éviterons ici. Si une branche relie un noeud ni à un noeud nj
plus bas, on dira que ni est un ancêtre de nj. Une
propriété fondamentale d'un arbre est qu'un noeud n'a qu'un seul
père. Enfin, un noeud peut contenir une ou plusieurs valeurs, et on
parlera alors d'arbres étiquetés et de la valeur (ou des
valeurs) d'un noeud. Les arbres binaires
sont des arbres tels que les noeuds ont au plus 2 fils. La hauteur, on dit aussi la profondeur d'un noeud est la longueur
du chemin qui le joint à la racine, ainsi la racine est elle même de
hauteur 0, ses fils de hauteur 1 et les autres noeuds de hauteur
supérieure à 1.
Un exemple d'arbre très utilisé en informatique est la
représentation des expressions arithmétiques et plus généralement
des termes dans la programmation symbolique. Nous traiterons ce cas
dans le chapitre sur l'analyse syntaxique, et nous nous restreindrons
pour l'instant au cas des arbres de recherche ou des arbres de tri.
Toutefois, pour montrer l'aspect fondamental de la structure d'arbre,
on peut tout de suite voir que les expressions arithmétiques calculées
dans la section 3.4 se représentent
simplement par des arbres comme dans la figure
4.2 pour (* (+ 5 (* 2 3)) (+ (* 10 10) (* 9
9))). Cette représentation contient l'essence de la structure
d'expression arithmétique et fait donc abstraction de toute notation
préfixée ou postfixée.
Figure 4.2 : Représentation d'une expression arithmétique par un arbre
4.1 Files de priorité
Un premier exemple de structure arborescente est la structure de tas
(heap1
)utilisée pour représenter des files de priorité.
Donnons d'abord une vision intuitive d'une file de priorité.
On suppose, comme au paragraphe 3.2, que des gens
se présentent au guichet d'une banque avec un numéro écrit sur un
bout de papier représentant leur degré de priorité. Plus ce nombre
est élevé, plus ils sont importants et doivent passer rapidement.
Bien sûr, il n'y a qu'un seul guichet ouvert, et l'employé(e) de la
banque doit traiter rapidement tous ses clients pour que tout le monde
garde le sourire. La file des personnes en attente s'appelle une file de priorité. L'employé de banque doit donc savoir faire
rapidement les 3 opérations suivantes: trouver un maximum dans la
file de priorité, retirer cet élément de la file, savoir ajouter un
nouvel élément à la file. Plusieurs solutions sont envisageables.
La première consiste à mettre la file dans un tableau et à trier la
file de priorité dans l'ordre croissant des priorités. Trouver un
maximum et le retirer de la file est alors simple: il suffit de
prendre l'élément de droite, et de déplacer vers la gauche la borne
droite de la file. Mais l'insertion consiste à faire une passe du
tri par insertion pour mettre le nouvel élément à sa place, ce qui
peut prendre un temps O(n) où n est la longueur de la file.
Une autre méthode consiste à gérer la file comme une simple file du
chapitre précédent, et à rechercher le maximum à chaque fois.
L'insertion est rapide, mais la recherche du maximum peut prendre un
temps O(n), de même que la suppression.
Figure 4.3 : Représentation en arbre d'un tas
Une méthode élégante consiste à gérer une structure d'ordre
partiel grâce à un arbre. La file de n éléments est
représentée par un arbre binaire contenant en chaque noeud un
élément de la file (comme illustré dans la figure
4.3). L'arbre vérifie deux propriétés importantes:
d'une part la valeur de chaque noeud est supérieure ou égale à
celle de ses fils, d'autre part l'arbre est quasi complet, propriété
que nous allons décrire brièvement. Si l'on divise l'ensemble des
noeuds en lignes suivant leur hauteur, on obtient en général dans un
arbre binaire une ligne 0 composée simplement de la racine, puis
une ligne 1 contenant au plus deux noeuds, et ainsi de suite (la
ligne i contenant au plus 2i noeuds). Dans un arbre quasi complet
les lignes, exceptée peut être la dernière, contiennent toutes un
nombre maximal de noeuds (soit 2i). De plus les feuilles de la
dernière ligne se trouvent toutes à gauche, ainsi tous les noeuds
internes sont binaires, excepté le plus à droite de l'avant
dernière ligne qui peut ne pas avoir de fils droit. Les feuilles sont
toutes sur la dernière et éventuellement l'avant dernière ligne.
On peut numéroter cet arbre en largeur d'abord, c'est à dire dans
l'ordre donné par les petits numéros figurant au dessus de la figure
4.3. Dans cette numérotation on vérifie que tout
noeud i a son père en position ë i/2 û, le fils
gauche du noeud i est 2i, le fils droit 2i + 1. Formellement,
on peut dire qu'un tas est un tableau a contenant n entiers (ou
des éléments d'un ensemble totalement ordonné) satisfaisant les
conditions:
| 2 £ 2i £ n | Þ | a[2i] ³ a[i] |
| 3£ 2i+1 £ n | Þ | a[2i+1] ³ a[i]
| |
|
Ceci permet d'implémenter cet arbre dans un tableau a (voir
figure 4.4) où le numéro de chaque noeud donne
l'indice de l'élément du tableau contenant sa valeur.
Figure 4.4 : Représentation en tableau d'un tas
L'ajout d'un nouvel élément v à la file consiste à incrémenter
n puis à poser a[n] = v. Ceci ne représente plus un tas car la
relation a[n/2] ³ v n'est pas nécessairement satisfaite. Pour
obtenir un tas, il faut échanger la valeur contenue au noeud n et
celle contenue par son père, remonter au père et réitérer jusqu'à
ce que la condition des tas soit vérifiée. Ceci se programme par
une simple itération (cf. la figure 4.5).
static void ajouter (int v) {
++nTas;
int i = nTas - 1;
while (i > 0 && a [(i - 1)/2] <= v) {
a[i] = a[(i - 1)/2];
i = (i - 1)/2;
}
a[i] = v;
}
Figure 4.5 : Ajout dans un tas
Figure 4.6 : Suppression dans un tas
On vérifie que, si le tas a n éléments, le nombre
d'opérations n'excédera pas la hauteur de l'arbre correspondant. Or
la hauteur d'un arbre binaire complet de n noeuds est log n. Donc
Ajouter ne prend pas plus de O(log n) opérations.
On peut remarquer que l'opération de recherche du maximum est
maintenant immédiate dans les tas. Elle prend un temps constant
O(1).
static int maximum () {
return a[0];
}
Considérons l'opération de suppression du premier élément de la
file. Il faut alors retirer la racine de l'arbre représentant la
file, ce qui donne deux arbres! Le plus simple pour reformer un seul
arbre est d'appliquer l'algorithme suivant: on met l'élément le plus
à droite de la dernière ligne à la place de la racine, on compare
sa valeur avec celle de ses fils, on échange cette valeur avec celle
du vainqueur de ce tournoi, et on réitère cette opération jusqu'à
ce que la condition des tas soit vérifiée. Bien sûr, il faut faire
attention, quand un noeud n'a qu'un fils, et ne faire alors qu'un
petit tournoi à deux. Le placement de la racine en bonne position
est illustré dans la figure 4.6.
static void supprimer () {
int i, j;
int v;
a[0] = a[nTas - 1];
--nTas;
i = 0; v = a[0];
while (2*i + 1 < nTas) {
j = 2*i + 1;
if (j + 1 < nTas)
if (a[j + 1] > a[j])
++j;
if (v >= a[j])
break;
a[i] = a[j]; i = j;
}
a[i] = v;
}
A nouveau, la suppression du premier élément de la file ne
prend pas un temps supérieur à la hauteur de l'arbre représentant
la file. Donc, pour une file de n éléments, la suppression prend
O(log n) opérations. La représentation des files de priorités par des
tas permet donc de faire les trois opérations demandées: ajout,
retrait, chercher le plus grand en log n opérations. Ces
opérations sur les tas permettent de faire le tri HeapSort.
Ce tri peut être considéré comme alambiqué, mais il a la bonne
propriété d'être toujours en temps
n log n (comme le Tri fusion, cf page X).
HeapSort se divise en deux phases, la première consiste à
construire un tas dans le tableau à trier, la seconde à répéter
l'opération de prendre l'élément maximal, le retirer du tas en le
mettant à droite du tableau. Il reste à comprendre comment on peut
construire un tas à partir d' un tableau quelconque. Il y a une
méthode peu efficace, mais systématique. On remarque d'abord que
l'élément de gauche du tableau est à lui seul un tas. Puis on
ajoute à ce tas le deuxième élément avec la procédure
Ajouter que nous venons de voir, puis le troisième, .... A
la fin, on obtient bien un tas de N éléments dans le tableau
a à trier. Le programme est
static void heapSort () {
int i;
int v;
nTas = 0;
for (i = 0; i < N; ++i)
ajouter (a[i]);
for (i = N - 1; i >= 0; --i) {
v = maximum();
supprimer();
a[i] = v;
}
}
Si on fait un décompte grossier des opérations, on
remarque qu'on ne fait pas plus de N log N opérations pour
construire le tas, puisqu'il y a N appels à la procédure
Ajouter. Une méthode plus efficace, que nous ne décrirons pas ici,
qui peut être traitée à titre d'exercice,
permet de construire le tas en O(N) opérations.
De même, dans la deuxième phase, on ne fait pas plus de N log N
opérations pour défaire les tas, puisqu'on appelle N fois la
procédure Supprimer. Au total, on fait O(N log N)
opérations quelle que soit la distribution initiale du tableau
a, comme dans le tri fusion. On peut néanmoins remarquer que
la constante qui se trouve devant N log N est grande, car on appelle
des procédures relativement complexes pour faire et défaire les tas.
Ce tri a donc un intérêt théorique, mais il est en pratique bien moins
bon que Quicksort ou le tri Shell.
4.2 Borne inférieure sur le tri
Il a été beaucoup question du tri. On peut se demander s'il est
possible de trier un tableau de N éléments en moins de N log N
opérations. Un résultat ancien de la théorie de l'information
montre que c'est impossible si on n'utilise que des comparaisons.
En effet, il faut préciser le modèle de calcul que l'on considère.
On peut représenter tous les tris que nous avons rencontrés par des
arbres de décision. La figure 4.7 représente
un tel arbre pour le tri par insertion sur un tableau de 3 éléments.
Chaque noeud interne pose une question sur la comparaison entre 2
éléments. Le fils de gauche correspond à la réponse négative, le
fils droit à l'affirmatif. Les feuilles représentent la permutation
à effectuer pour obtenir le tableau trié.
Théorème 1
Le tri de N éléments, fondé uniquement sur les comparaisons des
éléments deux à deux, fait au moins O(N log N) comparaisons.
Démonstration
Tout arbre de décision pour trier N
éléments a N! feuilles représentant toutes les permutations
possibles. Un arbre binaire de N! feuilles a une hauteur de l'ordre
de log N! » N log N par la formule de Stirling.
Corollaire 1 HeapSort et le tri fusion sont optimaux (asymptotiquement).
En effet, ils accomplissent le nombre de comparaisons donné
comme borne inférieure dans le théorème précédent. Mais, nous
répétons qu'un tri comme Quicksort est aussi très bon en moyenne.
Le modèle de calcul par comparaisons donne une borne inférieure,
mais peut-on faire mieux dans un autre modèle? La réponse est oui,
si on dispose d'informations annexes comme les valeurs possibles des
éléments ai à trier. Par exemple, si les valeurs sont comprises
dans l'intervalle [1, k], on peut alors prendre un tableau b
annexe de k éléments qui contiendra en bj le nombre de ai
ayant la valeur j. En une passe sur a, on peut remplir le tableau
k, puis générer le tableau a trié en une deuxième passe en ne
tenant compte que de l'information rangée dans b. Ce tri prend O(k
+ 2 N) opérations, ce qui est très bon si k est petit.
Figure 4.7 : Exemple d'arbre de décision pour le tri
4.3 Implémentation d'un arbre
Jusqu'à présent, les arbres sont apparus comme des entités
abstraites ou n'ont été implémentés que par des tableaux en
utilisant une propriété bien particulière des arbres complets. On
peut bien sûr manipuler les arbres comme les listes avec des
enregistrements et des pointeurs. Tout noeud sera représenté par un
enregistrement contenant une valeur et des pointeurs vers ses fils.
Une feuille ne contient qu'une valeur. On peut donc utiliser des
enregistrements avec variante pour signaler si le noeud est interne ou
une feuille. Pour les arbres binaires, les deux fils seront
représentés par les champs filsG, filsD et il sera plus
simple de supposer qu'une feuille est un noeud dont les fils gauche et
droit ont une valeur vide.
class Arbre {
int contenu;
Arbre filsG;
Arbre filsD;
Arbre (int v, Arbre a, Arbre b) {
contenu = v;
filsG = a;
filsD = b;
}
}
Pour les arbres quelconques, on peut gagner plus d'espace
mémoire en considérant des enregistrements variables. Toutefois, en
Pascal, il y a une difficulté de typage à considérer des noeuds
n-aires (ayant n fils). On doit considérer des types différents pour
les noeuds binaires, ternaires, ... ou un gigantesque
enregistrement avec variante. Deux solutions systématiques sont
aussi possibles: la première consiste à considérer le cas n
maximum (comme pour les arbres binaires)
class Arbre {
int contenu;
Arbre[] fils;
Arbre (int v, int n) {
contenu = v;
fils = new Arbre[n];
}
}
la deuxième consiste à enchaîner les fils dans une liste
class Arbre {
int contenu;
ListeArbres fils;
}
class ListeArbres {
Arbre contenu;
ListeArbres suivant;
}
Avec les tailles mémoire des ordinateurs actuels, on se
contente souvent de la première solution. Mais, si les contraintes de
mémoire sont fortes, il faut se rabattre sur la deuxième. Dans une
bonne partie de la suite, il ne sera question que d'arbres binaires,
et nous choisirons donc la première représentation avec les champs
filsG et filsD.
Considérons à présent la construction d'un nouvel arbre binaire
c à partir de deux arbres a et b. Un noeud sera
ajouté à la racine de l'arbre et les arbres a et b
seront les fils gauche et droit respectivement de cette racine. La
fonction correspondante prend la valeur du nouveau noeud, les fils
gauche et droit du nouveau noeud. Le résultat sera un pointeur vers
ce noeud nouveau. Voici donc comment créer l'arbre de gauche de la
figure 4.8.
class Arbre {
int contenu;
Arbre filsG;
Arbre filsD;
Arbre (int v, Arbre a, Arbre b) {
contenu = v;
filsG = a;
filsD = b;
}
public static void main(String args[]) {
Arbre a5, a7;
a5 = new Arbre (12, new Arbre (8, new Arbre (6, null, null), null),
new Arbre (13, null, null));
a7 = new Arbre (20, new Arbre (3, new Arbre (3, null, null), a5),
new Arbre (25, new Arbre (21, null, null),
new Arbre (28, null, null)));
imprimer (a7);
}
Une fois un arbre créé, il est souhaitable de pouvoir
l'imprimer. Plusieurs méthodes sont possibles. La plus élégante
utilise les fonctions graphiques du Macintosh drawString,
moveTo, lineTo. Une autre consiste à utiliser une
notation linéaire avec des parenthèses. C'est la notation infixe utilisée couramment si les noeuds internes sont des
opérateurs d'expressions arithmétique. L'arbre précédent s'écrit
alors
((3 3 ((6 8 nil) 12 13)) 20 (21 25 28))
Utilisons une méthode plus rustique en imprimant en
alphanumérique sur plusieurs lignes. Ainsi, en penchant un peu la
tête vers la gauche, on peut imprimer l'arbre précédent comme suit
20 25 28
21
3 12 13
8
6
3
La procédure d'impression prend comme argument l'arbre à
imprimer et la tabulation à faire avant l'impression, c'est à dire
le nombre d'espaces. On remarquera que toute la difficulté de la
procédure est de bien situer l'endroit où on effectue un retour à
la ligne. Le reste est un simple parcours récursif de l'arbre en se
plongeant d'abord dans l'arbre de droite.
static void imprimer (Arbre a) {
imprimer (a, 0);
System.out.println ();
}
static void imprimer1 (Arbre a, int tab) {
if (a != null) {
System.out.print (leftAligned (3, a.contenu + "") + " ");
imprimer1 (a.filsD, tab + 8);
if (a.filsG != null) {
System.out.println ();
for (int i = 1; i <= tab; ++i)
System.out.print (" ");
}
imprimer1 (a.filsG, tab);
}
}
static String leftAligned (int size, String s) {
StringBuffer t = new StringBuffer (s);
for (int i = s.length(); i < size; ++i)
t = t.append(" ");
return new String (t);
}
Nous avons donc vu comment représenter un arbre dans un
programme, comment le construire, et comment l'imprimer. Cette
dernière opération est typique: pour explorer une structure de
donnée récursive (les arbres), il est naturel d'utiliser des
procédures récursives. C'est à nouveau une manière non seulement
naturelle, mais aussi très efficace dans le cas présent.
Comme pour les listes (cf. page X), la
structure récursive des programmes manipulant des arbres découle de
la définition des arbres, puisque le type des arbres binaires
vérifie l'équation:
Arbre = {Arbre_vide} È
Arbre ×
Element × Arbre
|
Comme pour l'impression, on peut calculer le nombre de
noeuds d'un arbre en suivant la définition récursive du type des
arbres:
static int taille (Arbre a) {
if (a == null) (* a = Arbre_vide *)
return 0;
else (* a Î Arbre × Element × Arbre *)
return 1 + taille (a.filsG) + taille (a.filsD);
}
L'écriture itérative dans le cas des arbres est en
général impossible sans utiliser une pile. On vérifie que, pour les
arbres binaires qui ne contiennent pas de noeuds unaires, la taille
t, le nombre de feuilles Nf et le nombre de noeuds internes Nn
vérifient t = Nn + Nf et Nn = 1 + Nf.
4.4 Arbres de recherche
La recherche en table et le tri peuvent être aussi traités avec des
arbres. Nous l'avons vu implicitement dans le cas de Quicksort. En
effet, si on dessine les partitions successives obtenues par les
appels récursifs de Quicksort, on obtient un arbre. On introduit
pour les algorithmes de recherche d'un élément dans un ensemble
ordonné la notion d'arbre binaire de recherche
celui-ci aura la propriété
fondamentale suivante: tous les noeuds du sous-arbre gauche d'un noeud
ont une valeur inférieure (ou égale) à la sienne et tous les noeuds du
sous-arbre droit ont une valeur supérieure (ou égale) à la valeur
du noeud lui-même (comme dans la figure
4.8). Pour la recherche en table, les
arbres de recherche ont un intérêt quand la table évolue très
rapidement, quoique les méthodes avec hachage sont souvent aussi
bonnes, mais peuvent exiger des contraintes de mémoire impossibles à
satisfaire. (En effet, il faut connaître
la taille maximale a priori d'une table de hachage). Nous allons voir
que le temps d'insertion d'un nouvel élément dans un arbre de
recherche prend un temps comparable au temps de recherche si cet arbre
est bien agencé. Pour le moment, écrivons les procédures
élémentaires de recherche et d'ajout d'un élément.
static Arbre recherche (int v, Arbre a) {
if (a == null || v == a.contenu)
return a;
else if (v < a.contenu)
return recherche (v, a.filsG);
else
return recherche (v, a.filsD);
}
static Arbre ajouter (int v, Arbre a) {
if (a == null)
a = new Arbre (v, null, null);
else if (v <= a.contenu)
a.filsG = ajouter (v, a.filsG);
else
a.filsD = ajouter (v, a.filsD);
return a;
}
Figure 4.8 : Ajout dans un arbre de recherche
A nouveau, des programmes récursifs correspondent à la
structure récursive des arbres. La procédure de recherche renvoie un
pointeur vers le noeud contenant la valeur recherchée, null si
échec. Il n'y a pas ici d'information associée à la clé recherchée
comme au chapitre 1. On peut bien sûr associer une information à la
clé recherchée en ajoutant un champ dans l'enregistrement décrivant
chaque noeud. Dans le cas du bottin de téléphone, le champ
contenu contiendrait les noms et serait du type String;
l'information serait le numéro de téléphone.
La recherche teste d'abord si le contenu de la racine est égal à la
valeur recherchée, sinon on recommence récursivement la recherche dans
l'arbre de gauche si la valeur est plus petite que le contenu de la
racine, ou dans l'arbre de droite dans le cas contraire. La procédure
d'insertion d'une nouvelle valeur suit le même schéma. Toutefois dans
le cas de l'égalité des valeurs, nous la rangeons ici par convention
dans le sous arbre de gauche. La procédure ajouter modifie
l'arbre de recherche. Si nous ne voulons pas le modifier, nous pouvons
adopter comme dans le cas des listes la procédure suivante, qui
consomme légèrement plus de place, laquelle place peut être récupérée
très rapidement par le glaneur de cellules:
static Arbre ajouter (int v, Arbre a) {
if (a == null)
return new Arbre (v, null, null);
else if (v <= a.contenu)
return new Arbre (v, ajouter (v, a.filsG), a.filsD);
else
return new Arbre (v, a.filsG, ajouter (v, a.filsG));
}
Le nombre d'opérations de la recherche ou de l'insertion dépend de
la hauteur de l'arbre. Si l'arbre est bien équilibré, pour un arbre
de recherche contenant N noeuds, on effectuera O(log N)
opérations pour chacune des procédures. Si l'arbre est un peigne,
c'est à dire complètement filiforme à gauche ou à droite, la hauteur
vaudra N et le
nombre d'opérations sera O(N) pour la recherche et l'ajout. Il
apparaît donc souhaitable d'équilibrer les arbres au fur et à mesure
de l'ajout de nouveaux éléments, ce que nous allons voir dans la
section suivante.
Enfin, l'ordre dans lequel sont rangés les noeuds dans un arbre de
recherche est appelé ordre infixe.
Il correspond au petit
numéro qui se trouve au dessus de chaque noeud dans la figure
4.8. Nous avons déjà vu dans le cas de
l'évaluation des expressions arithmétiques (cf page
X) l'ordre préfixe,
dans
lequel tout noeud reçoit un numéro d'ordre inférieur à celui de
tous les noeuds de son sous-arbre de gauche, qui eux-mêmes ont des
numéros inférieurs aux noeuds du sous-arbre de droite. Finalement,
on peut considérer l'ordre postfixe
qui ordonne d'abord le
sous-arbre de gauche, puis le sous-arbre de droite, et enfin le noeud.
C'est un bon exercice d'écrire un programme d'impression
correspondant à chacun de ces ordres, et de comparer l'emplacement
des différents appels récursifs.
4.5 Arbres équilibrés
La notion d'arbre équilibré a été introduite en 1962 par deux
russes Adel'son-Vel'skii et Landis, et depuis ces arbres sont connus
sous le nom d'arbres AVL. Il y a maintenant beaucoup de variantes plus
ou moins faciles à manipuler. Au risque de paraître classiques et
vieillots, nous parlerons principalement des arbres AVL. Un arbre AVL
vérifie la propriété fondamentale suivante: la différence entre
les hauteurs des fils gauche et des fils droit de tout noeud ne peut
excéder 1. Ainsi l'arbre de gauche de la figure
4.8 n'est pas équilibré. Il viole la
propriété aux noeuds numérotés 2 et 7, tous les autres noeuds validant
la propriété. Les arbres représentant des tas, voir figure
4.5 sont trivialement équilibrés.
On peut montrer que la hauteur d'un arbre AVL de N noeuds est de
l'ordre de log N, ainsi les temps mis par
la procédure Recherche vue page
X seront en O(log N).
Il faut donc maintenir l'équilibre de tous les noeuds au fur et à
mesure des opérations d'insertion ou de suppression d'un noeud dans
un arbre AVL. Pour y arriver, on suppose que tout noeud contient un
champ annexe bal contenant la différence de hauteur entre le
fils droit et le fils gauche. Ce champ représente donc la balance ou
l'équilibre entre les hauteurs des fils du noeud, et on s'arrange
donc pour maintenir -1 £ a.bal £ 1 pour tout noeud
pointé par a.
L'insertion se fait comme dans un arbre de recherche standard, sauf
qu'il faut maintenir l'équilibre. Pour cela, il est commode que
la fonction d'insertion retourne une valeur représentant la
différence entre la nouvelle hauteur (après l'insertion) et
l'ancienne hauteur (avant l'insertion). Quand il peut y avoir un
déséquilibre trop important entre les deux fils du
noeud où l'on insère un nouvel élément, il faut recréer un
équilibre par une rotation simple (figure 4.9) ou
une rotation double (figure 4.10). Dans ces
figures, les rotations sont prises dans le cas d'un rééquilibrage de
la gauche vers la droite. Il existe bien sûr les 2 rotations
symétriques de la droite vers la gauche. On peut aussi remarquer que
la double rotation peut se réaliser par une suite de deux rotations
simples. Dans la figure 4.10, il suffit de
faire une rotation simple de la droite vers la gauche du noeud A,
suivie d'une rotation simple vers la droite du noeud B. Ainsi en
supposant déjà écrites les procédures de rotation rotD vers
la droite et rotG vers la gauche, la procédure d'insertion
s'écrit
Figure 4.9 : Rotation dans un arbre AVL
static Arbre ajouter (int v, Arbre a) {
return ajouter1 (v, a).p2;
}
static Paire ajouter1 (int v, Arbre a) {
int incr, r;
Paire p;
r = 0;
if (a == null) {
a = new Arbre (v, null, null);
a.bal = 0;
r = 1;
} else {
if (v <= a.contenu) {
p = ajouter1 (v, a.filsG);
incr = -p.p1;
a.filsG = p.p2;
} else {
p = ajouter1 (v, a.filsD);
incr = p.p1;
a.filsD = p.p2;
}
a.bal = a.bal + incr;
if (incr != 0 && a.bal != 0)
if (a.bal < -1)
/* La gauche est trop grande */
if (a.filsG.bal < 0)
a = rotD (a);
else {
a.filsG = rotG (a.filsG);
a = rotD (a);
}
else
if (a.bal > 1)
/* La droite est trop grande */
if (a.filsD.bal > 0)
a = rotG (a);
else {
a.filsD = rotD (a.filsD);
a = rotG (a);
}
else
r = 1;
}
return new Paire (r, a);
}
static class Paire {
int p1;
Arbre p2;
Paire (int r, Arbre a) {
p1 = r;
p2 = a;
}
}
Figure 4.10 : Double rotation dans un arbre AVL
Clairement cette procédure prend un temps O(log N). On
vérifie aisément qu'au plus une seule rotation (éventuellement
double) est nécessaire lors de l'insertion d'un nouvel élément. Il
reste à réaliser les procédures de rotation. Nous ne considérons
que le cas de la rotation vers la droite, l'autre cas s'obtenant par
symétrie.
static Arbre rotD (Arbre a) {
Arbre b;
int bA, bB, bAnew, bBnew;
b = a;
a = a.filsG;
bA = a.bal; bB = b.bal;
b.filsG = a.filsD;
a.filsD = b;
// Recalculer le champ a.bal
bBnew = 1 + bB - Math.min(0, bA);
bAnew = 1 + bA + Math.max(0, bBnew);
a.bal = bAnew;
b.bal = bBnew;
return a;
}
Il y a un petit calcul savant pour retrouver le champ
représentant l'équilibre après rotation. Il pourrait être
simplifié si nous conservions toute la hauteur du noeud dans un
champ. La présentation avec les champs bal permet de garder
les valeurs possibles entre -2 et 2, de tenir donc sur 3 bits, et
d'avoir le reste d'un mot machine pour le champ contenu. Avec
la taille des mémoires actuelles, ce calcul peut se révéler
surperflu. Toutefois, soient h(a), h(b) et h(c) les hauteurs
des arbres a, b et c de la figure 4.9. En
appliquant la définition du champ bal, les nouvelles valeurs
b'(A) et b'(B) de ces champs aux noeuds A et B se calculent en
fonction des anciennes valeurs b(A) et b(B) par
| b'(B) | = | h(c) - h(b) |
| | = | h(c) - 1 - é h(a), h(b) ù
+ 1 + é h(a), h(b) ù - h(b) |
| | = | b(B) +1 + é h(a) - h(b), 0 ù |
| | = | 1 + b(B) - ë 0, b(A) û |
| | | |
| b'(A) | = | 1 + é h(b), h(c) ù - h(a) |
| | = | 1 + h(b) - h(a) + é 0, h(c) - h(b) ù |
| | = | 1 + b(A) + é 0, b'(B) ù
| | |
Les formules pour la rotation vers la gauche s'obtiennent par
symétrie. On peut même remarquer que le champ bal peut tenir
sur 1 bit pour signaler si le sous-arbre a une hauteur égale ou non
à celle de son sous-arbre ``frère''. La suppression d'un élément
dans un arbre AVL est plus dure à programmer, et nous la laissons en
exercice. Elle peut demander jusqu'à O(log N) rotations.
Les arbres AVL sont délicats à programmer à cause
des opérations de rotation. On peut montrer que les rotations
deviennent inutiles si on donne un peu de flexibilité dans le
nombre de fils des noeuds. Il existe des arbres de recherche 2-3 avec
2 ou 3 fils. L'exemple le plus simple est celui des arbres 2-3-4
amplement décrits dans le livre de Sedgewick [47].
Un exemple d'arbre 2-3-4 est décrit dans la figure
4.11. La propriété fondamentale d'un tel arbre de
recherche est la même que pour les noeuds binaires: tout noeud doit
avoir une valeur supérieure ou égale à celles contenues dans ses
sous-arbres gauches, et une valeur inférieure (ou égale) à celles
de ses sous-arbres droits. Les noeuds ternaires contiennent 2 valeurs,
la première doit être comprise entre les valeurs des sous-arbres
gauches et du centre, la deuxième entre celles des sous-arbres du
centre et de droite. On peut deviner aisément la condition pour les
noeuds à 4 fils.
L'insertion d'un nouvel élément dans un arbre 2-3-4 se fait en
éclatant tout noeud quaternaire que l'on rencontre comme décrit dans
la figure 4.12. Ces opérations sont locales et ne font
intervenir que le nombre de fils des noeuds. Ainsi, on garantit que
l'endroit où on insère la nouvelle valeur n'est pas un noeud
quaternaire, et il suffit de mettre la valeur dans ce noeud à
l'endroit désiré. (Si la racine est quaternaire, on l'éclate en 3
noeuds binaires). Le nombre d'éclatements maximum peut être log N
pour un arbre de N noeuds. Il a été mesuré qu'en moyenne très
peu d'éclatements sont nécessaires.
Les arbres 2-3-4 peuvent être programmés en utilisant des arbres
binaires bicolores. On s'arrange pour que chaque branche puisse avoir
la couleur rouge ou noire (en trait gras sur notre figure
4.13).
Il suffit d'un indicateur booléen dans chaque noeud pour dire si la
branche le reliant à son père est rouge ou noire. Les noeuds
quaternaires sont représentés par 3 noeuds reliés en noir. Les
noeuds ternaires ont une double représentation possible comme décrit
sur la figure 4.13. Les opérations d'éclatement se
programment alors facilement, et c'est un bon exercice d'écrire la
procédure d'insertion dans un arbre bicolore.
Figure 4.11 : Exemple d'arbre 2-3-4
Figure 4.12 : Eclatement d'arbres 2-3-4
Figure 4.13 : Arbres bicolores
4.6 Programmes en Caml
(* Ajouter à un tas, avec une structure enregistrement *)
type 'a tas =
{ mutable cardinal: int;
tas: 'a vect };;
let ajouter v t =
t.cardinal <- t.cardinal + 1;
let a = t.tas in
let nTas = t.cardinal in
let i = ref (nTas - 1) in
if !i >= vect_length a
then failwith "tas plein" else
while !i > 0 && a.((!i - 1) / 2) <= v do
a.(!i) <- a.((!i - 1) / 2);
i := (!i - 1) / 2
done;
a.(!i) <- v;;
(* Ajouter à un tas, voir page X *)
let nTas = ref 0;;
let ajouter v a =
incr nTas;
let i = ref (!nTas - 1) in
while !i > 0 && a.((!i - 1) / 2) <= v do
a.(!i) <- a.((!i - 1) / 2);
i := (!i - 1) / 2
done;
a.(!i) <- v;;
(* Maximum d'un tas, voir page X *)
let maximum t = t.tas.(0);;
(* Supprimer dans un tas,
voir page X *)
let supprimer t =
t.cardinal <- t.cardinal - 1;
let a = t.tas in
let nTas = t.cardinal in
a.(0) <- a.(nTas);
let i = ref 0
and v = a.(0)
and j = ref 0 in
begin
try
while 2 * !i + 1 < nTas do
j := 2 * !i + 1;
if !j + 1 < nTas && a.(!j + 1) > a.(!j)
then j := !j + 1;
if v >= a.(!j) then raise Exit;
a.(!i) <- a.(!j);
i := !j
done
with Exit -> ()
end;
a.(!i) <- v;;
(* HeapSort, voir page X *)
let heapsort a =
let n = vect_length a - 1 in
let t = {cardinal = 0; tas = a} in
for i = 0 to n do ajouter a.(i) t done;
for i = n downto 0 do
let v = maximum t in
supprimer t;
a.(i) <- v
done;;
(* Déclaration d'un arbre binaire, voir page X *)
type 'a arbre = Vide | Noeud of 'a noeud
and 'a noeud =
{contenu: 'a; filsG: 'a arbre; filsD: 'a arbre};;
(* Déclaration d'un arbre n-aire, voir page X *)
type 'a arbre = Vide | Noeud of 'a noeud
and 'a noeud = {contenu: 'a; fils: 'a arbre vect};;
(* Cas n-aire, les fils sont
implémentés par une liste d'arbres. *)
type 'a arbre = Vide | Noeud of 'a noeud
and 'a noeud = {contenu: 'a; fils: 'a arbre list};;
(* Ajouter dans un arbre *)
let nouvel_arbre v a b =
Noeud {contenu = v; filsG = a; filsD = b};;
let main () =
let a5 =
nouvel_arbre 12
(nouvel_arbre 8 (nouvel_arbre 6 Vide Vide) Vide)
(nouvel_arbre 13 Vide Vide) in
nouvel_arbre 20
(nouvel_arbre 3 (nouvel_arbre 3 Vide Vide) a5)
(nouvel_arbre 25
(nouvel_arbre 21 Vide Vide)
(nouvel_arbre 28 Vide Vide));;
(* Impression d'un arbre, voir page X *)
#open "printf";;
let imprimer_arbre a =
let rec imprimer1 a tab =
match a with
Vide -> ()
| Noeud {contenu = c; filsG = fg; filsD = fd} ->
printf "%3d " c; imprimer1 fd (tab + 8);
if fg <> Vide then
printf "\n%s" (make_string tab ` `);
imprimer1 fg tab;;
in
imprimer1 a 0; print_newline();;
(* Taille d'un arbre, voir page X *)
let rec taille = function
Vide -> 0
| Noeud {filsG = fg; filsD = fd; _} ->
1 + taille fg + taille fd;;
(* Arbre de recherche,
voir page X *)
let rec recherche v a =
match a with
Vide -> Vide
| Noeud
{contenu = c; filsG = fg; filsD = fd} ->
if c = v then a else
if c < v then recherche v fg
else recherche v fd;;
(* Ajouter, purement fonctionnel,
voir page X *)
let rec ajouter v a =
match a with
Vide -> nouvel_arbre v Vide Vide
| Noeud
{contenu = c; filsG = fg; filsD = fd} ->
if v <= c
then nouvel_arbre c (ajouter v fg) fd
else nouvel_arbre c (ajouter v fd) fg;;
(* Ajouter avec effet de bord,
voir page \pageref{prog:recherche-arb-ajouter-fonctionnel}} *)
type 'a arbre = Vide | Noeud of 'a noeud
and 'a noeud =
{mutable contenu: 'a;
mutable filsG: 'a arbre;
mutable filsD: 'a arbre};;
let nouvel_arbre v a b =
Noeud {contenu = v; filsG = a; filsD = b};;
let rec ajouter v a =
match a with
Vide -> nouvel_arbre v Vide Vide
| Noeud
({contenu = c; filsG = fg; filsD = fd}
as n) ->
if v <= c
then n.filsG <- ajouter v fg
else n.filsD <- ajouter v fd;
a;;
(* Ajouter, purement fonctionnel avec un autre type d'arbres *)
type 'a arbre = Vide | Noeud of 'a arbre * 'a * 'a arbre;;
let nouvel_arbre v a b =
Noeud (a, v, b);;
let rec ajouter v a =
match a with
Vide -> nouvel_arbre v Vide Vide
| Noeud (fg, c, fd) ->
if v <= c
then nouvel_arbre c (ajouter v fg) fd
else nouvel_arbre c (ajouter v fd) fg;;
(* Arbres AVL, voir page X *)
type 'a avl = Vide | Noeud of 'a noeud
and 'a noeud =
{ mutable balance: int;
mutable contenu: 'a;
mutable filsG: 'a avl;
mutable filsD: 'a avl };;
let nouvel_arbre bal v a b =
Noeud
{balance = bal; contenu = v;
filsG = a; filsD = b};;
#open "format";;
let rec print_avl = function
Vide -> ()
| Noeud
{balance = bal; contenu = v;
filsG = a; filsD = b} ->
open_box 1; print_string "(";
print_int bal; print_string ": ";
print_int v; print_space();
print_avl a; print_space(); print_avl b;
print_cut(); print_string ")";
close_box();;
install_printer "print_avl";;
(* Rotation dans un AVL, voir page X *)
let rotD a =
match a with
Vide -> failwith "rotD"
| Noeud
({balance = bB; contenu = v;
filsG = A; filsD = c} as nB) as B ->
match A with
Vide -> failwith "rotD"
| Noeud
({balance = bA; contenu = v;
filsG = a; filsD = b} as nA) ->
nA.filsD <- B;
nB.filsG <- b;
let bBnew = bB + 1 - min 0 bA in
let bAnew = bA + 1 + max 0 bBnew in
nA.balance <- bAnew;
nB.balance <- bBnew;
A;;
(* Rotation dans un AVL, voir page X *)
let rotG a =
match a with
Vide -> failwith "rotG"
| Noeud
({balance = bA; contenu = v;
filsG = c; filsD = B} as nA) as A ->
match B with
| Vide -> failwith "rotG"
| Noeud
({balance = bB; contenu = v;
filsG = a; filsD = b} as nB) ->
nA.filsD <- a;
nB.filsG <- A;
let bAnew = bA - 1 - max 0 bB in
let bBnew = bB - 1 + min 0 bAnew in
nA.balance <- bAnew;
nB.balance <- bBnew;
B;;
(* Ajout dans un AVL, voir page X *)
let rec ajouter v a =
match a with
Vide -> (nouvel_arbre 0 v Vide Vide, 1)
| Noeud
({balance = bal; contenu = c;
filsG = fg; filsD = fd} as noeud) ->
let diff =
if v <= c then begin
let (a, incr) = ajouter v fg
in
noeud.balance <- noeud.balance - incr;
noeud.filsG <- a;
incr
end else begin
let (a, incr) = ajouter v fd
in
noeud.balance <- noeud.balance + incr;
noeud.filsD <- a;
incr
end in
if diff <> 0 && noeud.balance <> 0 then
if noeud.balance < -1 then begin
match fg with
Vide -> failwith "Vide"
| Noeud {balance = b; _} ->
if b < 0 then (rotD a, 0)
else begin
noeud.filsG <- rotG fg; (rotD a, 0)
end
end else
if noeud.balance > 1 then begin
match fd with
Vide -> failwith "Vide"
| Noeud {balance = b; _} ->
if b > 0 then (rotG a, 0)
else begin
noeud.filsD <- rotD fd; (rotG a, 0)
end
end
else (a, 1)
else (a, 0);;
- 1
- Le mot heap a malheureusement un autre sens
en Pascal: c'est l'espace dans lequel sont allouées les variables
dynamiques référencées par un pointeur après l'instruction
new. Il sera bien clair d'après le contexte si nous parlons de
tas au sens des files de priorité ou du tas de Pascal pour allouer
les variables dynamiques.