[0-3]+
L’automate est
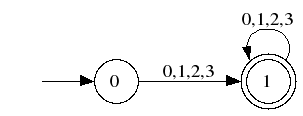
| ⋆⋆⋆ |
Dans cet exercice on opère sur le langage des mots
construits à partir des chiffres de 0 à 3.
On accepte les zéros superflus en tête de l’écriture des entiers
naturels.
Question 1. Donner une expression régulière et un automate fini déterministe qui définissent l’écriture en base 4 des entiers naturels.
L’expression régulière est [0-3]+
L’automate est
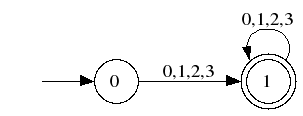 |
Question 2. Donner une expression régulière et un automate fini déterministe qui définissent les suites finies (possiblement vides) de chiffres croissantes au sens large.
L’expression régulière est 0*1*2*3*.
L’automate est
 |
Question 3. Donner une expression régulière qui définit les suites finies non-vides de chiffres croissantes au sens large.
Il apparaît que l’on peut distinguer quatre cas, selon
le premier chiffre qui existe toujours.
L’expression régulière est
0+1*2*3*|1+2*3*|2+3*|3+.
|
Question 4. Donner une expression régulière et un automate fini pas nécessairement déterministe qui définissent les entiers pairs exprimés en base 4.
Il s’agit des entiers dont le dernier chiffre est 0 ou 2.L’expression régulière est donc 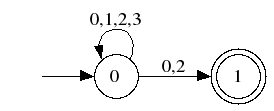 |
Question 5. Donner un automate déterministe qui définit le langage de la question précédente.
Le plus sûr paraît de déterminiser l’automate réponse de
la question précédente.
 |
Cette partie décrit l’application aux listes de l’algorithme (classique) du tri pivot. Le problème aborde une difficulté parfois passée sous silence : les éléments des listes ne sont pas forcément deux à deux distincts.
En diverses occasions nous utiliserons la notion d’élément médian parmi n éléments a1, a2, …, an. Un élément médian e est défini comme l’un des ai qui est tel que l’on peut séparer les ai (moins e) en deux séquences b1, b2, …, bm et c1, c2, …, ct, telles que e majore (au sens large) les bi, e minore (au sens large) les ci, et m et t sont aussi proches que possible. Plus précisément, si n est impair, alors m et t sont égaux, tandis que si m est pair, m et t diffèrent de un. Selon notre définition, l’élément médian existe toujours, même quand les ai ne sont pas deux à deux distincts, mais n’est pas nécessairement unique. Par exemple, si la séquence est « 1, 4, 0, 1 » alors n’importe lequel des éléments de valeur 1 est un élément médian (par exemple a0), la séquence des éléments majorés étant par exemple « 0 » (a2), et la séquence des éléments minorés « 4, 1 » (a1, a3).
Soit la classe List des cellules de listes (d’entiers) :
Question 6. Écrire une méthode
static List lessThan(int x, List c) qui renvoie la liste des
éléments de c qui sont strictement inférieurs à l’entier x.
|
static List lessThan(int x, List c){
if (c == null)
return null ;
else if (c.val < x)
return new List(c.val, lessThan(x, c.next)) ;
else
return lessThan(x, c.next) ;
} |
On définit l’interface Pred suivante.
C’est-à-dire que les objets des classes qui implémentent l’interface Pred
possèdent une méthode test qui prend un entier en argument et
renvoie un booléen.
Question 7. Écrire une méthode static List filter(Pred p, List c)
qui renvoie la liste des éléments de c qui vérifient le
prédicat p, c’est-à-dire qui sont tels que
p.test(x) renvoie true.
|
static List filter(Pred p, List c) {
if (c == null)
return null ;
else if (p.test(c.val))
return new List (c.val, filter(p, c.next)) ;
else
return filter(p, c.next) ;
} |
Question 8.
Définir une classe Lt qui implémente l’interface Pred
et qui est telle que :
Lt(int x) prend un entier en argument.
test(int y) renvoie true si y < x et
false autrement.
|
class Lt implements Pred {
private int x ;
Lt(int x) { this.x = x ; }
public boolean test(int y) { return y < x ; }
} |
Question 9. Récrire lessThan (question 6) en une ligne, en utilisant
les deux questions précédentes.
|
static List lessThan(int x, List c) { return filter(new Lt(x), c) ; } |
Question 10. Reprendre la technique de la question
précédente, pour cette fois écrire
une méthode static List greaterEqual(int x, List c) qui renvoie
la liste des éléments de c qui sont supérieurs ou égaux
à x.
D’abord définir une classe Ge qui réalise le prédicat y ≥ x.
class Ge implements Pred {
private int x ;
Ge (int x) { this.x = x ; }
public boolean test(int y) { return y >= x ; }
} Et ensuite appeler filter.
static List greaterEqual(int x, List c) { return filter(new Ge(x), c) ; } |
Question 11. Soient deux listes c1 et c2, triées en ordre
croissant et telles que les éléments de la première liste sont tous
inférieurs aux éléments de la seconde liste.
Sous ces hypothèses, Écrire une
méthode static List compose(List c1, List c2)
qui renvoie la
liste triée en ordre croissant formée des éléments de c1 et c2.
Compte tenu des hypothèses, compose est la
concaténation des listes.
static List compose(List c1, List c2){
if (c1==null)
return c2 ;
else
return new List(c1.val, compose(c1.next,c2)) ;
} |
Nous allons maintenant implémenter un algorithme de tri classique dit tri pivot (dit aussi quicksort). Le principe est le suivant :
c n’est pas vide, son premier élément est le pivot.
Question 12.
Écrire une méthode static List sort(List c) qui renvoie
une copie de la liste c triée en ordre croissant selon la
méthode du pivot. Attention, la description du tri pivot donnée est
approximative.
|
static List sort(List c){
if (c==null)
return null ;
else {
int a = c.val ;
List cLT = lessThan(a, c.next) ; // NB c.next
List cGE = greaterEqual(a, c.next) ; // NB c.next
return compose (sort(cLT), new List(a, sort(cGE))) ;
}
} |
Question 13. Dans cette question on demande la complexité du tri pivot (nombre de comparaisons entre éléments) dans quelques cas particuliers. On demande un ordre de grandeur asymptotique (notation Θ, poly page 168).
a) Le tri est effectué sur une liste déjà triée de longueur n.
Le calcul de cLt et cGE se fait toujours au prix de
2(n−1) comparaisons.
Dans les conditions de la question,
cLt est toujours vide, et
cGE est une liste croissante de taille n−1.
On a donc les équations de coût :
|
b) On suppose que la liste à trier comprend n=2p−1 éléments deux à deux distincts, et que le pivot est toujours un élément médian.
Dans ce cas favorable on a les équations de coût :
|
c) On suppose que la liste à trier contient n fois un élément particulier, la longueur de cette liste étant de l’ordre de n.
|
Le tri pivot est en O(n2) dans le cas général (n longueur de la
liste). C’est intuitivement
assez clair et relativement facile à montrer par induction (parce que
k n12 + k n22 ≤ k(n1 + n2)2).
Cela vaut donc aussi pour le cas particulier ici traité. Soit e l’élément particulier. Si la liste à trier contient n fois e, une des deux listes fabriquées contiendra n (le pivot ne vaut pas e) ou n−1 (le pivot vaut e) fois l’élément e. La fabrication de cette liste coûte toujours au moins n−1 comparaisons. Une des suites d’appels récursifs est donc de profondeur au moins n−1, chacun des appels effectuant au moins n−1, n−2, …, jusqu’à 1 comparaisons. Le coût du tri est donc minoré par la somme des n−1 premiers entiers, et donc est en Ω(n2). Au final, le tri est en Θ(n2). |
Question 14. On peut améliorer très significativement l’efficacité du
tri dans le cas 13-c) ci-dessus, en divisant la liste à
trier non plus en deux mais en trois parties.
Écrire une nouvelle méthode static List sort(List c) améliorée selon
cette idée.
L’idée est de répartir les éléments de la liste c
en trois listes, selon qu’ils sont strictement inférieurs au pivot,
égaux au pivot, ou strictement supérieurs au pivot.
Il nous faut donc deux nouvelles classes de prédicats.
class Gt implements Pred {
private int x ;
Gt(int x) { this.x = x ; }
public boolean test(int y) { return y > x ; }
}
class Eq implements Pred {
private int x ;
Gt(int x) { this.x = x ; }
public boolean test(int y) { return y = x ; }
} Puis voici le tri :
static List sort(List c) {
if (c == null)
return null ;
else {
int a = c.val ;
List cLT = sort(filter(new Lt(a), c.next)) ;
List cEQ = filter(new Eq(a), c.next) ;
List cGT = sort(filter(new Gt(a), c.next)) ;
return compose(cLT, compose(new List(a,cEQ), cGT)) ;
}
} |
Question 15. Montrer que la nouvelle méthode sort
(question précédente)
peut mieux se comporter que l’ancienne (question 12),
dans le cas examiné à la question 13-c).
|
Il suffit de décrire un exemple favorable.
On suppose d’abord que le premier pivot est l’élément particulier e,
on décompose la liste en trois pour un coût linéaire.
Il reste ensuite deux listes à trier dont les longueurs sont, par
exemple,
toutes deux d’ordre n.
Puis, d’après 13-b), il est possible d’atteindre une complexité
de l’ordre de n logn qui domine. Plus simplement on peut examiner le cas de n éléments identiques, on a d’une part un coût quadratique et d’autre un coût linéaire. |
La structure de liste, même triée, ne facilite pas l’opération de recherche d’un élément.
Question 16. Majorer le mieux possible l’ordre de grandeur asymptotique (notation O) de l’opération de recherche dans une liste triée.
| La recherche est en O(n), comme la recherche dans le cas le pire où l’élément recherché majore strictement tous les éléments de la liste. |
On se donne une structure d’arbre binaire de recherche légèrement
étendue. Voici la définition de la classe Tree des cellules
de ces arbres.
Un arbre Tree représente un multi-ensemble (ensemble avec
répétition possible des éléments) : le multi-ensemble
des étiquettes de toutes ses cellules.
Par la suite, nous parlerons parfois du multi-ensemble a quand
a est un objet Tree, ainsi que du multi-ensemble c
quand c est un objet List.
La structure proposée ici est une légère extension des arbres binaires de
recherche du cours dans le sens que l’on impose que, si a est un
arbre non-vide (a != null), alors
a.val est supérieur ou égal à
toutes les étiquettes du sous-arbre de gauche a.left
et inférieur ou égal à toutes les étiquettes du sous-arbre de
droite a.right.
Question 17.
Écrire une méthode static boolean mem(int x, Tree a)
qui teste la présence de x dans le multi-ensemble a.
Majorer le mieux possible (notation O) le coût de mem en fonction d’une
caractéristique pertinente de l’arbre a.
|
La méthode est identique à celle des arbres binaires de
recherche du cours.
static Tree mem(int x, Tree a) {
if (a == null)
return false ;
else if (x < a.val)
return mem(x, a.left) ;
else if (x > a.val)
return mem(x, a.right) ;
else
return true ;
} La complexité est en O(d) où d est la profondeur de l’arbre
définie comme la taille du plus long chemin possible dans l’arbre
(zéro pour l’arbre vide, un pour une feuille, etc.)
|
Question 18. Écrire une méthode static Tree treeOfList(List c)
qui construit l’arbre représentant le multi-ensemble c.
On s’inspirera du tri pivot (question 12).
|
static Tree treeOfList(List c) {
if (c == null)
return null ;
else {
int a = c.val ;
return
new Tree (filter(new Lt(a), c.next),
a,
filter(new Ge(a), c.next))) ;
}
} |
Question 19.
Écrire une méthode inverse de la précédente,
static List listOfTree(Tree a) qui renvoie la liste triée
représentant le même multi-ensemble que a.
On impose un coût linéaire en la taille de a.
|
static List scan(Tree a, List k) {
if (a == null)
return k ;
else {
k = scan(a.right, k) ;
return scan(a.left, new List(a.val, k)) ;
}
}
static List listOfTree(Tree a) {
return scan(a, null) ;
} |
Question 20. Dans cette question on suppose que la liste List c
est triée en ordre croissant.
On cherche alors à créer efficacement un arbre équilibré qui
représente le multi-ensemble c.
a)
Écrire une méthode static int [] arrayOfList(List c)
qui renvoie un tableau trié dont les éléments sont ceux de la
liste c. On impose une complexité linéaire en la longueur
de la liste c.
|
Il s’agit de maintenir l’ordre des éléments.
static int [] arrayOfList(List c) {
// Calcul de la longueur de la liste
int len = 0 ;
for (List p = c ; p != null ; p = p.next) len++ ;
// Allouer puis remplir le tableau
int [] t = new int[len] ;
int k = 0 ;
for (List p = c ; p != null ; p = p.next) {
t[k] = p.val ; k++ ;
}
} |
b)
Écrire une méthode static Tree treeOfArray(int [] t)
qui renvoie un arbre dont les étiquettes sont les
éléments de t.
On supposera que t est trié en ordre croissant.
L’idée est alors la suivante : produire un arbre dont la
racine est étiquetée par un élément médian du tableau t.
En outre on impose,
t notée n,
|
// Renvoie l'arbre du multi-ensemble t[g…d[
static Tree build(int [] t, int g, int d) {
if (g >= d)
return null ;
else {
int m = (g+d)/2 ;
Tree tg = build(t, g, m) ;
Tree td = build(t, m+1, d) ;
return new Tree(tg, t[m], td) ;
}
static Tree treeOfArray(int [] t) {
return build(t, 0, t.length) ;
} La complexité linéaire de build provient de ce que
un appel à build effectue deux appels récursifs
sur des tableaux dont la somme des tailles est n−1, ainsi qu’un
nombre constant d’opérations élémentaires.
|
c) Prouver que votre méthode treeOfArray renvoie bien
un arbre équilibré au sens des AVL.
Indication : normalement, la profondeur des arbres produits
s’exprime simplement en fonction de l’unique entier p tel que
2p ≤ n < 2p+1, défini pour tout n > 0.
Pour ce qui est de la profondeur, on doit montrer que les
profondeurs des deux sous arbres tg et td diffèrent au plus
de un.
En fait on peut montrer le résultat plus fort suivant.
On pose n = d−g, n est la longueur du sous-tableau t[g…d[.
Pour tout entier n non nul, il existe un unique entier p, avec
build.
|
d) En combinant les solutions aux questions a) et b) on produit un arbre équilibré en un temps linéaire. Décrire une méthode plus directe qui se passe du tableau intermédiaire et estimer son coût. On demande une justification plausible de l’estimation et non pas un calcul exact.
Si on dispose d’une liste triée c, on trouve un élément
médian ainsi que les listes des éléments par lui minorés et majorés
pour un coût proportionnel à n, longueur de c.
On procède ensuite comme dans le cas du tableau, par deux appels
récursifs sur deux listes de taille moitié.On peut donc estimer le coût de cette construction en à peu près.
Soit un coût de l’ordre de n logn. |
Question 21. On s’intéresse maintenant à la suppression d’éléments de notre structure d’arbre.
a)
Écrire une méthode static int getMax(Tree a) qui
renvoie un élément maximal de a. Si un tel élément n’existe pas,
la méthode getMax est libre de faire ce que bon lui semble.
|
static int getMax(Tree a) {
if (a.right == null)
return a.val
else
return getMax(a.right) ;
} Si a est null (multi-ensemble vide), alors la méthode
échoue pas très proprement par déréférencement de null.
|
b) Écrire une méthode static Tree remove(int x, Tree a)
qui renvoie un arbre représentant le multi-ensemble représenté par
a, moins toutes les occurrences de x.
Une solution inspirée de remove des arbres binaires de recherche.
// Warning, we must have a != null
// Remove one occurrence of the maximum of a
static Tree removeMax(Tree a) {
if (a.right == null) // Found maximum : a.val
return a.left
else
return new Tree (a.left, a.val, removeMax(a.right))
}
static Tree remove(int x, Tree a) {
if (a == null)
return null ;
else if (x < a.val)
return new Tree(remove(x, a.left), a.val, a.right) ;
else if (x > a.val)
return new Tree(a.left, a.val, remove(x, a.right)) ;
else { // We have x == a.val
Tree tg = remove(x, a.left) ;
Tree td = remove(x, a.right) ;
if (tg == null)
return td ;
else
return new Tree (removeMax(tg), getMax(tg), td) ;
}
} On note que removeMax n’enlève qu’une des occurrences du
maximum.Une solution moins élégante est d’écrire
un static Tree remove(int x, Tree a) {
while (mem(x,a)) {
a = removeOne(x, a) ;
}
return a ;
} |
This document was translated from LATEX by HEVEA.