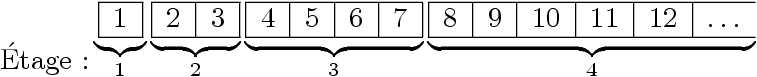Ensembles
-
Avec des listes,
- Avec des arbres,
- Un cas particulier, le tas.
Réalisation des ensembles avec les listes
On peut représenter le ensembles par des listes.
Il suffit de maintenir la condition :
Les éléments d’un ensemble sont deux à deux distincts.
Il faut donc pouvoir déterminer l’égalité de deux éléments.
Dans la suite, nos éléments sont des int, mais cela pourrait
facilement être des objets quelconques (par redéfinition de la
méthode equals des Object).
La classe des listes (d’entiers)
Air connu…
class List {
int val ;
List next ;
List (int val, List next) {
this.val = val ; this.next = next ;
}
}
Opérations élémentaires
-
Test d’appartenance.
static boolean mem(int x, List p) {
for ( ; p != null ; p = p.next) {
if (x == p.val) return true ;
}
return false ;
}
- Ajout
static List add(int a, List p) {
if (mem(a, p)) {
return p ;
} else {
return new List (a, p) ;
}
}
Opération ensembliste : union
-
Récursif.
static List union(List p, List q) {
if (p == null) {
return q ;
} else {
return add(p.val, union(p.next, q)) ;
}
}
- Itératif.
static List union(List p, List q) {
List r = q ;
for ( ; p != null ; p = p.next) {
r = add(p.val, r) ;
}
return r ;
}
Bilan des coût
Quel est alors le coût asymptotique dans le cas le pire :
-
Du test d’appartenance ? O(n)
(penser à l’échec, compter les appels de fonction).
- De l’ajout ? O(n) (comme
mem).
- De l’union (de deux ensembles de cardinaux
n et m) ? O(n × (n+m)) (n fois
add).
Une idée
Normaliser les listes : représenter un ensemble par la liste triées
(ordre croissant) de ses éléments.
Appartenance
On peut utiliser l’ancienne méthode mem
où une méthode un peu améliorée.
static boolean mem(int x, List p) {
if (p == null || x < p.val) {
return false ;
} else {
return p.val == x || mem(x, p.next) ;
}
}
Ajout et union
-
Ajout ? Insertion dans une liste triée
(cf. insertion sort).
- Union ? Fusion de deux listes triées
(cf. merge sort).
Bilan des coûts
| | mem | add | union |
| Liste | O(n) | O(n) | O(n2) |
| Liste triée | O(n) | O(n) | O(n) |
Remarquer L’implémentation « liste triée » favorise l’opération
ensembliste, mais n’améliore pas les autres opérations.
Représenter les ensembles avec les arbres
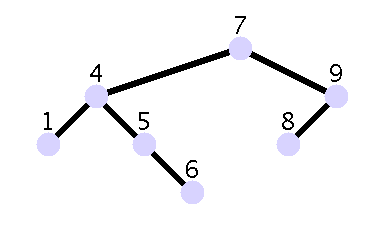
On définit les arbres binaires de recherche :
-
L’arbre vide est un ABR, ses clefs sont ∅.
- Si T0 et T1 sont des ABR, de clefs respectives
C0 et C1 et :
-
x majore (strictement) toutes les clefs de C0 ;
- x minore (strictement) toutes les clefs de C1 ;
alors (T0, x, T1) est un ABR et ses clefs sont C0 ∪ {x }
∪ C1.
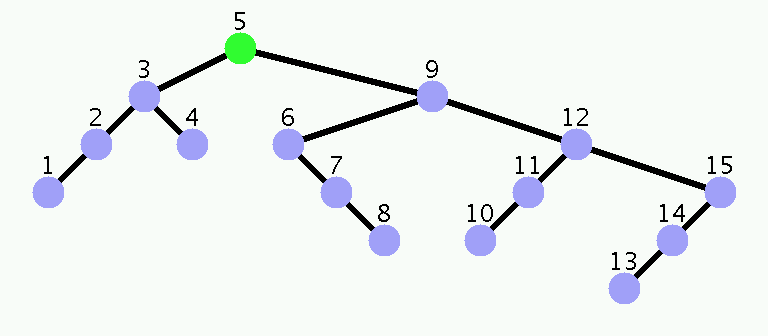
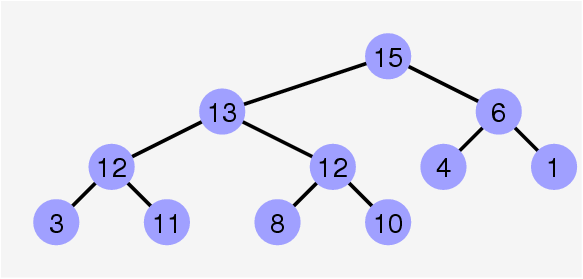
Un exemple d’arbre binaire de recherche
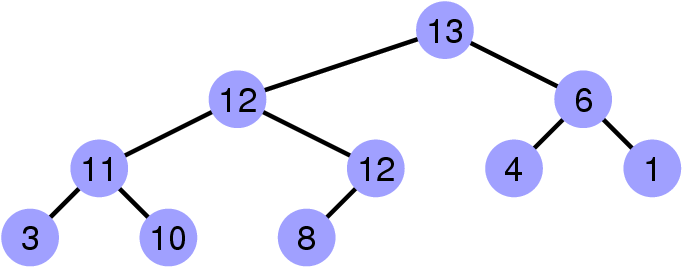
Un contre-exemple d’arbre binaire de recherche
Classe Tree des arbres binaires de
recherche
class Tree {
int key ;
Tree left, right ;
Tree (Tree left, int key, Tree right) {
this.left = left ; this.right = right ;
this.key = key ;
}
Tree (int key) {
this.key = key ; left = right = null ;
}
}
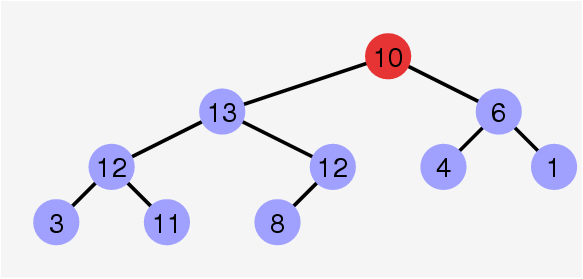
Test d’appartenance dans un ABR
C’est simple si on pense récursivement.
static boolean mem(int x, Tree t) {
if (t == null) {
return false ;
} else {
if (x < t.key) {
return mem(x, t.keft) ; // Chercher à gauche
} else if (x > t.key) {
return mem(x, t.right) ; // Chercher à droite
} else { // x == t.key
return true ; // Trouvé ici
}
}
}
Test d’appartenance dans un ABR II
Finalement assez simple à programmer itérativement,
penser que l’on suit un chemin dans un arbre.
static boolean mem(int x, Tree t) {
while (t != null) {
if (x < t.key) {
t = t.left ;
} else if (x > t.key) {
t = t.right ;
} else { // x == t.key
return true ;
}
}
return false ;
}
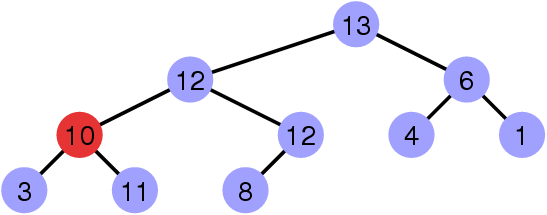
Ajouter un élément : insertion dans un ABR
static Tree add(int x, Tree t) {
if (t == null) {
return new Tree(x) ;
} else {
if (x < t.key) {
return new Tree (add(x, t.left), t.key, t.right) ;
// ajouter à gauche
} else if (v > t.key) {
return new Tree (t.left, t.key, add(x, t.right)) ;
// ajouter à droite
} else { // v == t.key, déjà là
return t ;
}
}
}
Programmation itérative possible, mais trop complexe.
Coût des deux opérations élémentaires
Il est facile de voir que le coût de mem et
add, est en O(h) où h est la hauteur de l’ABR.
Mais on veut borner le coût fonction de n cardinal de
l’ensemble…
Il faut donc exprimer la hauteur h en fonction du cardinal n.
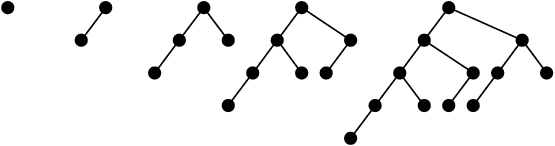
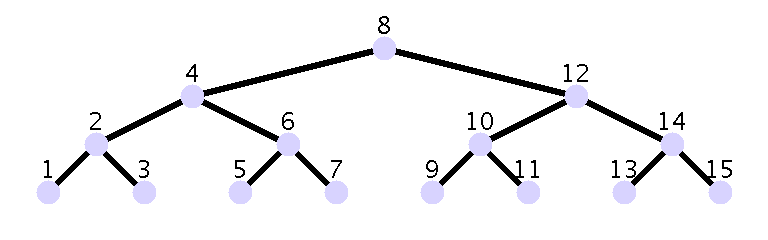
Un arbre (très) équilibré
Un arbre à peu près équilibré
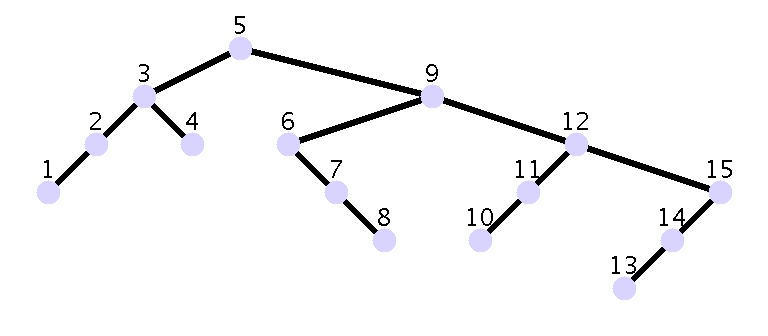
Un arbre (très) déséquilibré
Hauteur minimale d’un arbre binaire
Ou nombre maximal de sommets pour une hauteur
donnée : arbre binaire complet
| n ≤ 2h+1 − 1,
h ≥ log2(n+1)−1
|
Hauteur maximale d’un arbre binaire
Ou nombre minimal de sommets pour une hauteur
donnée : arbre dégénéré en liste.
Complexité en moyenne
Sur un univers E qui regroupe des événements e de probabilité
P(e), soit une fonction X(e).
L’espérance (moyenne) de X est définie par :
Par exemple :
-
e est un entier 1 ≤ k ≤ 2n,
- X est le nombre d’appels récursifs à
mem,
effectués lors du test d’appartenance de k
à la liste (triée) des entiers pairs compris entre 2 et 2n.
Appartenance dans les listes, coût en moyenne
-
Cas du
mem qui ne sait pas que la liste est triée.
Et donc :
- Cas du
mem qui sait que la liste est triée.
Et donc :
Deux résultats en moyenne, sur les ABR
Pour n tendant vers +∞…
-
La hauteur moyenne des arbres à n sommets est de l’ordre
de √n (pas de bol).
- La hauteur moyenne des arbres produits par addition de
1, …n, dans tous les ordres possibles est elle de l’ordre
de log(n).
Le second résultat nous permet plus ou moins de considérer qu’un arbre pris
au hasard est de hauteur log(n). Mais…
-
Le coût dans le cas le pire reste une hauteur en n.
- Et ce cas très déséquilibré est malheureusement assez probable
en pratique (addition de 1, 2, … n).
Les arbres AVL
Les arbres AVL (Adelson-Velinsky-Landis) sont des arbres binaires plus :
-
Les hauteurs des sous-arbres gauche et droit diffèrent au plus
de un
Une conséquence importante :
-
La hauteur d’un arbre AVL est en log(n).
| log2(1+n) ≤ 1+h ≤ α log2(2+n)
|
(avec α ≤ 1.44)
Diversion : explication rapide des bornes
-
La borne inférieure log2(1+n) ≤ 1+h est
vraie de tous les arbres binaires (un arbre de hauteur h à au plus
2h+1−1 nœuds).
- La borne supérieure est plus intéressante.
On considère l’arbre AVL Fh le plus petit possible pour une hauteur
donnée.
-
Hauteur zéro : arbre vide.
- Hauteur un : une feuille.
- Hauteur h+2 : Fh+2 = (Fh+1, x, Fh).
Arbre équilibré de hauteur maximale
Les équations définissant le nombre de sommets de l’arbre
de taille minimale pour h donné, sont donc.
| F(0) = 0,
F(1) = 1,
F(h+2) = 1 + F(h+1) + F(h)
|
Posons G(h) = F(h) + 1, il vient :
| G(0) = 1,
G(1) = 2,
G(h+2) = G(h+1) + G(h)
|
On trouve :
| G(h) = | | Φh + | | Φ−h,
avec Φ = | |
Au final la hauteur maximale d’un AVL est de l’ordre de
logΦ(n), donc de l’ordre de log2(n).
La vraie question des AVL : l’équilibre
Soit un AVL,
| On ajoute l’élément 5
Déséquilibre (à droite). | | On rétablit l’équilibre.
|
Comment garantir l’équilibre ?
Supposons écrite une méthode
balance(AVL left, int key, AVL right) qui renvoie un
arbre équilibré.
Alors c’est facile, (comme pour les ABR normaux).
static AVL add(int x, AVL t) {
if (t == null) {
return new AVL(x) ;
} else {
if (x < t.key) {
return balance(add(x, t.left), t.key, t.right) ;
} else if (v > t.key) {
return balance(t.left, t.key, add(x, t.right)) ;
} else {
return t ;
}
}
}
Classe des AVL
class AVL {
int key ;
private int h ; // Champ hauteur (pour éviter le recalcul)
AVL left, right ;
static int hauteur(AVL t) {
if (t == null) { return 0 ; }
else { return t.h ; }
}
AVL (AVL left, int key, AVL right) {
this.left = left ; this.right = right ; this.key = key ;
this.h = Math.max(hauteur(left), hauteur(right)) + 1 ;
}
AVL (int key) {this.key = key ; left = right = null ; h = 1 ;}
}
Il reste à écrire balance.
balance prend deux arbres left et right en argument,
avec (par construction)
−2 ≤ hauteur(left) − hauteur(right) ≤ 2
|
On suppose un déséquilibre, c’est à dire par ex.
hauteur(left) = hauteur(right) + 2
|
C’est à dire :
-
On a ajouté un élément dans le sous arbre de gauche,
- sa hauteur a augmenté (de un),
- alors qu’avant ajout le sous-arbre gauche était déjà plus
haut (de un) que le sous-arbre droit
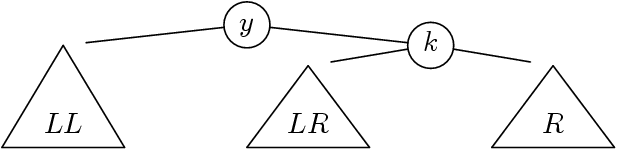
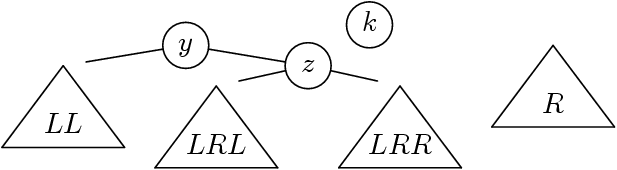
Analysons un peu encore
Notons L (arbre de gauche), k (clé) et R les arguments de
balance.
-
On note que (L,k,R) est un ABR, mais (possiblement) déséquilibré.
- On suppose le déséquilibre : h(L) = h(R)+2 et donc L = (LL, y, LR).
Notons H(R) = δ. Deux sous-cas :
-
Le sous-arbre, LL impose sa hauteur à L, c’est à dire h(LL) = δ+1
(et h(LR) = δ ou h(LR) = δ+1).
- Ou bien, LL n’impose pas sa hauteur à L, c’est à dire
h(LL) = δ et h(LR) = δ+1.
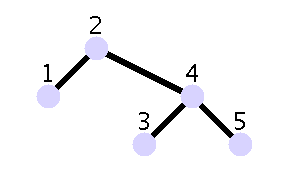
Premier cas
Supposons donc h(LL)= δ+1
(eth(LR)= δ ou h(LR)= δ+1).
Alors, l’arbre suivant est équilibré :
De hauteur δ+2 ou δ+3.
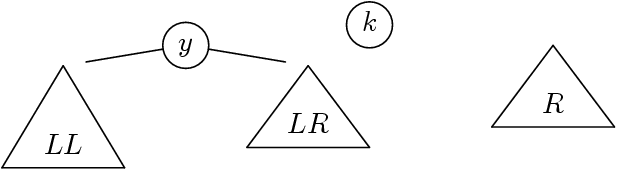
Second cas
Ce cas (δ = h(LL) < h(LR) = δ+1) entraîne
LR non-vide.
Alors, l’arbre suivant est équilibré
De hauteur δ+2.
Une remarque
Tout d’abord, un résultat,
si h(L) = h(R)+2, nous savons produire un AVL équivalent
à l’ABR déséquibré (L,x,R), et ceci en temps constant.
Dans le cas de l’ajout, la hauteur finale de l’AVL est toujours
δ+2, car le cas h(LL) = h(LR) = δ+2 ne peut pas se produire
(sinon, l’arbre avant ajout serait déséquibré).
Cette hauteur est égale à celle de l’arbre avant ajout
On en déduit que l’équilibrage se produit au plus une
fois lors d’un ajout.
Dans un souci de complétude
static AVL balance(AVL left, int val, AVL right) {
int hl = hauteur(left), hr = hauteur(right);
if (hl > hr + 1) { // => left != null
if (hauteur(left.left) >= hauteur(left.right))
return
new AVL(left.left,left.key,new AVL (left.right,val,right));
else // => left.right != null
return
new AVL(new AVL (left.left,left.key,left.right.left),
left.right.key,
new AVL (left.right.right,val,right));
} else if (hr > hl + 1) { // Même chose en symétrique
…
} else
return new AVL (left,val,right);
}
Conclusion temporaire
Le minimum à savoir.
Dans le même ordre d’idée
Les arbres equilibrés permettent une implémentation efficace des
associations (amphi 04), cette fois persistantes.
-
Il suffit d’ajouter un champ
val dans la définition des
cellules d’arbre.
class TreeEnv { // Association des chaînes aux entiers
String key ;
int val ;
TreeEnv left, right ;
…
}
- On retrouver la valeur associée à une clé par un genre
de
mem.
static int get(TreeEnv env, String key, int val) {
…
}
- On ajoute une association par un genre de
add.
static TreeEnv put(TreeEnv env, String key, int val) {
…
}
La méthode put renvoie env augmenté de la nouvelle
association, env n’est pas modifé. - Et ici il faut remarquer la différence avec la signature par exemple
des tables de hachage.
void put(K key, V value)
Les ABR de la bibliothèque
De façon surprenante, les TreeSet de Java, sont des ensembles
impératifs (non-persistants), dommage.
Prenons le cas des ABR, on trouve les premiers cas par induction.
static Tree remove(Tree t, int v) {
if (t == null) {
return null ;
} else if (v < t.key) {
return new Tree (remove(t.left, v), t.key, t.right) ;
} else if (v > t.key) {
return new Tree (t.left, t.key, remove(t.right, v)) ;
} else if (t.right == null) {
return t.left ;
} else {// Ici v == t.val, t.right != null
…
Le dernier cas n’est pas immédiat : il faut mélanger t.left et
t.right en un seul ABR.
Exemple : enlever la racine
L’idée, remplacer la racine par le minimun du sous-arbre droit.
Trouver/enlever le minimum
-
Trouver : à gauche toute !
static int getMin(Tree t) {
while (t.left != null) {
t = t.left ;
}
return t.key ;
}
- Enlever, à gauche encore !
static Tree removeMin(Tree t) {
if (t.left == null) {
return t.right ;
} else {
return new Tree (removeMin(t.left), t.key, t.right) ;
}
}
Remplacer la racine
Voci le code manquant de remove.
static Tree remove(Tree t, int v) {
…
} else { // Ici v == t.val, t.right != null
int min = getMin(t.right) ;
return new Tree(t.left, min, removeMin(t.right)) ;
}
}
Et les AVL ?
Remplacer, dans remove et removeMin,
tous les appels du constructeur new Tree(ℓ, v, r)
par des appels de méthode balance(ℓ, v, r).
Correction ?
Le déséquilibre entre ℓ et r est
limité à 2 au plus.
Opération ensemblistes
Réaliser par exemple l’union de deux deux ensembres représentés
par les ABR equilibrés T1 et T2.
Une première méthode simple :
Parcourir l’arbre T1 pour ajouter ses éléments à T2
(avec la méthode add).
Coût (T1 et T2 possédant n éléments) :O(n logn) (n fois add dans un arbre de taille au plus 2n)
Une autre méthode (pour les ABR)
Union de T1 et T2
-
Si T1 est vide, renvoyer T2.
- Si T2 est vide, renvoyer T1.
- Sinon T1 = (L1, x, R1),
-
Calculer les ABR L2 et R2, définis comme formés des
éléments de T2 respectivement < et > à x.
- Renvoyer l’ABR (L1 ∪ L2, x, R1 ∪ R2)
Remarquer
-
Si T1 et T2 sont le même ensemble le coût est en O(n).
- Généralisable aux AVL, avec des résultats satisfaisants en pratique.
Programmation de union
Suit directement l’algorithme.
static Tree union(Tree t1, Tree t2) {
if (t1 == null) return t2 ;
else if (t2 == null) return t1 ;
else {
Tree l1 = t1.left, r1 = t1.right ;
int x = t1.key ;
Tree l2 = splitLt(x, t2), r2 = splitGt(x, t2) ;
return new Tree (union(l1, l2), x, union(r1, r2)) ;
}
}
Programmation de splitLt
Renvoie l’ensemble des éléments de t qui sont < à x.
static Tree splitLt(int x, Tree t) {
if (t == null) return null ;
else {
if (t.key < x) { // Ici t.left < x
return new Tree(t.left, t.key, splitLt(x, t.right))
} else if (t.key > x) {
// Cas symétrique
} else { // t.key == x
return t.left ;
}
}
}
Coût, (approche heuristique)
Supposons les arbres équilibrés.
Le coût d’un appel à union
est dominé par celui des appels à splitLt et splitGt,
qui sont proportionels à la hauteur de t2.
En posant n = 2p,
Soit à peu près,
| U(2p) ∼ p + 2(p−1) + 4(p−2) + ⋯ 2p ∼ 2p+2.
|
Un cas particulier
-
Un ensemble dynamique : méthode
add.
- Avec une opération efficace de recherche/enlever le maximum
getMax, removeMax (ou le minimum, au choix à fixer à
l’avance).
On peut utiliser un arbre AVL, mais il existe une solution plus simple.
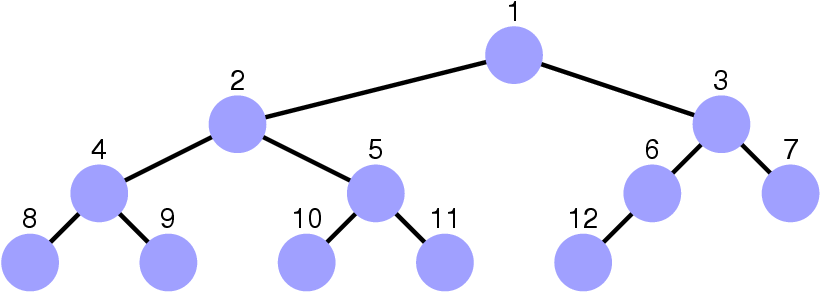
Les arbres (binaires) quasi-complets
-
Tous les étages sont remplis,
- Sauf, éventuellement, le dernier qui est
« tassé » vers la gauche.
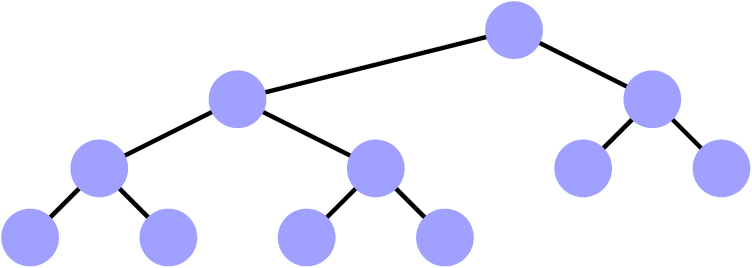
Exemples et contre-exemples
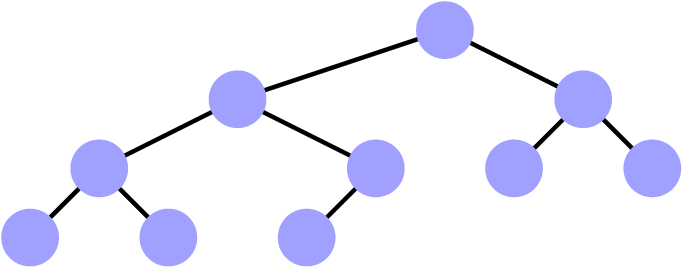 Oui
Oui
Noter : un des sommets de l’avant-dernier étage n’a
qu’un fils.
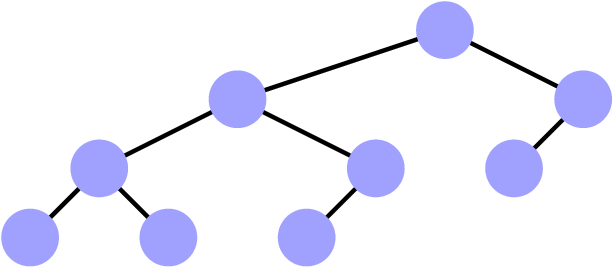 Non
Non, le troisième étage est incomplet.
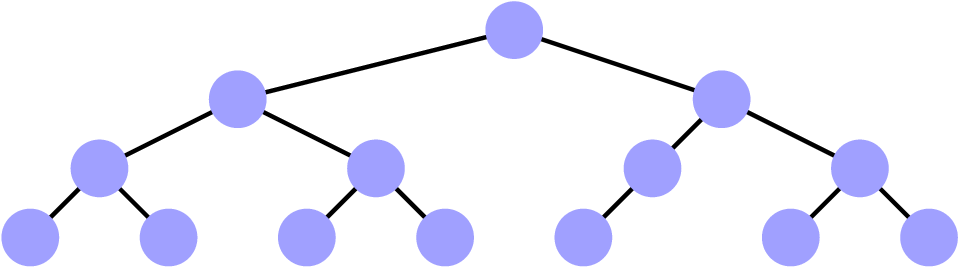 Non
Non, le dernier étage n’est pas « tassé ».
Arbres quasi-complets et tableaux
-
Numérotons les sommets selon un ordre « en largeur d’abord ».
- Et rangeons les sommets dans un tableau.
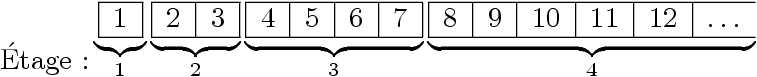
Arbres quasi-complets et tableaux
En fait les arbres quasi-complets sont exactement les arbres
représentables ainsi dans un tableau :
-
On choisit de ranger la racine de l’arbre dans la case
d’indice 1.
- Indice des fils du sommet d’indice i ?
-
Fils gauche : 2 × i.
- Fils droit : 2 × i + 1.
- Parent du sommet d’indice i (i > 1) ?
⌊i/2⌋.
- La case d’indice i est un sommet de l’arbre à n sommets ? 1 ≤ i ≤ n.
Bout de preuve
On numérote les sommets d’un arbre quasi-complet selon un parcours en
largeur d’abord :
-
Le d-ième étage comprend 2d−1 sommets (sauf le dernier
étage, c’est l’hypothèse « quasi-complet »).
- Le k-ième sommet du d-ième étage est donc d’indice :
| 20 + 21 + ⋯ + 2d−2 + k = 2d−1 + (k−1)
|
Reste à montrer qu’il
y a i−1 sommets entre un sommet d’indice i et son fils gauche
(si il existe).
Et en effet, il y a :
-
d’abord 2d−1 − k sommets de l’étage d (les « successeurs »),
- puis 2 × (k−1) sommets de l’étage d+1
(les fils des prédécesseurs de l’étage d).
Soit en tout i−1 sommets.
Bout de philosophie
-
Quelle est la hauteur d’un arbre quasi-complet à n sommets ?
- Avantage de la représentation en tableau.
-
Efficacité, économie de mémoire (avantage faible).
- Simplicité (notamment pour trouver le père d’un sommet).
- Avantage pédagogique : un arbre n’est pas nécessairement réalisé
en machine avec des objets, des flèches, etc.
(ici la « flèche » est remplacé par un « indice »).
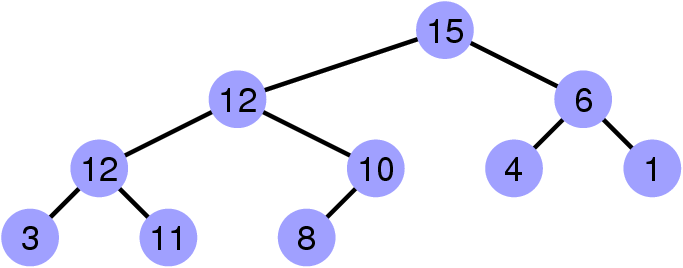
Le heap (tas)
Un tas est un arbre quasi-complet et :
-
Les sommets portent des clés ordonnées.
- La clé de tout sommet est supérieure ou égale à celles de ses
fils.
C’est un tas-max, il y aussi évidemment des tas-min.
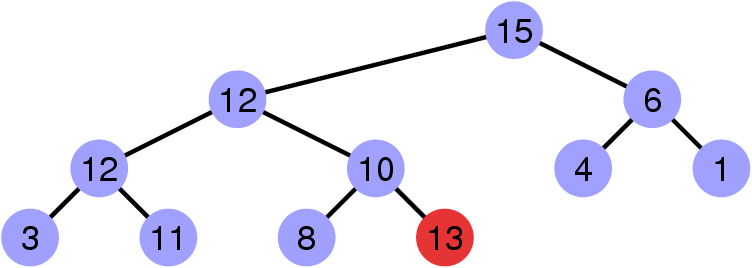
Contre-exemple
La propriété de heap est invalidée par le sommet de clé 13.
Le heap (tas)
Un tas est un arbre quasi-complet et :
-
Les sommets portent des clés ordonnées.
- La clé de tout sommet est supérieure ou égale à celles de ses
fils.
C’est un tas-max, il y aussi évidemment des tas-min.
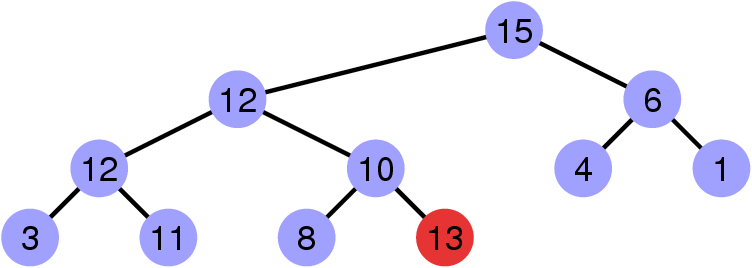
Contre-exemple
La propriété de heap est invalidée par le sommet de clé 13.
Classe Heap
Les tas (d’entiers) : encapsulage du tableau.
class Heap {
private int [] t ; // Tableau des sommets
private int n ; // Nombre de sommets
Heap(int sz) {
t = new int [sz+1] ;
n = 0 ;
}
…
}
Invalidation de la propriété de heap
La position d’indice n+1 dans le tableau est la feuille « suivante ».
(Ajout de 13.)
Restaurer la propriété de heap
Faire « remonter » le sommet invalidant.
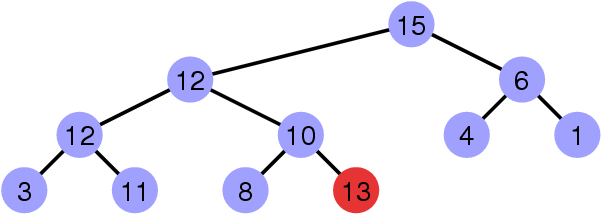
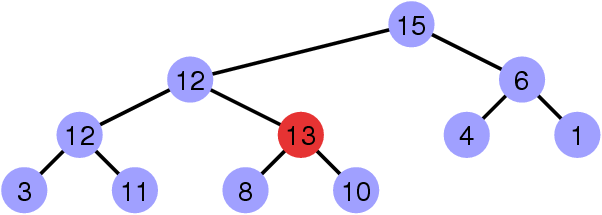


Faire « remonter » un sommet
void add(int x) {
n++ ;
int i = n ;
// Tant que i dans l'arbre et heap invalidé,
while (i > 1 && t[i/2] < x) { // NB: division euclidienne
t[i] = t[i/2] ; // Libérer la case i/2
i = i/2 ;
}
t[i] = x ;
}
Noter
Plutôt que d’échanger les cases, on fait remonter un trou.
-
Le maximum de toutes les clés se trouve… à la racine.
- Où enlever facilement un élément dans un heap représenté par un
tableau ? À la fin !
Donc,
-
Remplacer la racine par le dernier élément
(celui d’indice n dans le tableau).
- Restaurer la propriété de heap, (cette fois ci en descendant).
Restaurer le heap II
Faire « descendre » le sommet invalidant.
Le tas-outil
Les tas sont un outil efficace pour extraire des maxima (minima),
à la volée.
-
Ajouter un élément à n : log(n).
- Extraire le maximum parmi n : log(n).
- Efficacité brute raisonnable (quelques opérations sur entiers et
tableaux).
Il sont souvent une brique d’algorithmes plus complexes
(parcours de graphes, recherche de solutions optimales diverses).
Mais attention, les tas ne sont pas une bonne implémentation générale
des ensembles (ou des multi-ensembles).
Exemple de tas-outil
Par exemple : on trie facilement n éléments avec un tas :
-
Ajouter les éléments : nlog(n).
- Extraire les maxima : nlog(n).
Soit encore un tri en nlog(n).
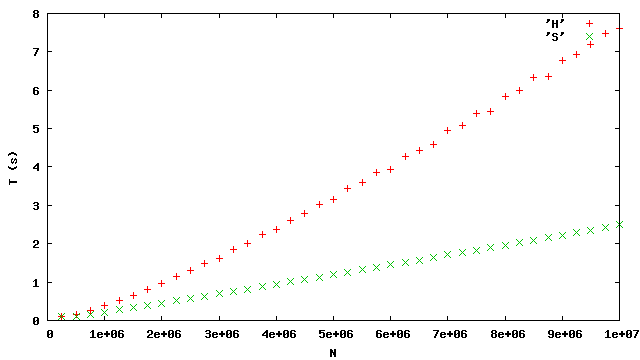
Performance de heapsort
Temps d’exécution de heapsort H
et du tri de la bibliothèque S (java.util.Arrays.sort).
Ce document a été traduit de LATEX par HEVEA