Programmer avec les listes Complexité des tris

Planche : 1

Programmer avec les listes

Échauffement
Tri des listes
- par insertion,
- par fusion.
Programmation objet
- ensembles persistents,
- ensembles mutables.

Planche : 2

Notre amie, la classe des (cellules de) listes

Déclaration
class List {
  int val ;
  List next ;

  List (int val, List next) {
    this.val = val ;
    this.next = next ;
  }
}
Usage : fabriquer la liste [1; 2; 3].
new List (1, new List (2, new List (3, null)))

Planche : 3

Opérations élémentaires

Il y en a trois.

La liste est elle vide ? p == null.
Prendre la tête, p.val.
Prendre la queue, p.next.

Boucle idiomatique

Traiter les éléments un par un, dans l’ordre.

for (List p = … ; p != null ; p = p.next) {
… // p.val est l'élément courant.
}

Planche : 4

Présentation théorique des listes

Les listes (de E) sont les solutions de l’équation:
L⟨E⟩ = { ∅ } ⋃ (E × L⟨E⟩)

Ce qui veut simplement dire, une liste est soit la liste vide, soit une paire composée d’un élément et d’uen autre liste.
Nous notons donc:
- La liste vide ∅,
- La liste non-vide (e; E).

Planche : 5

Lecture au clavier

Une liste d’entiers lus au clavier (ou dans un fichier), terminée par Ctrl-d (fin de fichier).

class IntReader { // Lecteur des int
  int read() { … }
  boolean hasNext() { … }
}

class List {
  …
  static List lireInts(IntReader in) {
    List r = null ;
    while (in.hasNext()) {
      r = new List (in.read(), r) ;
    }
    return r ;
  }
}

Bonus : Le code de l’exemple.

Planche : 6

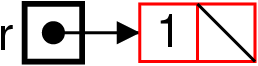
Fonctionnement

Initialement,

L’utilisateur entre 1,

puis 2,

puis 3,

etc.

Planche : 7

En résumé

L’utilisateur entre les valeurs i₁, …, i_n (et ferme l’entrée standard).
La boucle construit la liste :
  …
  r = new List(i₁, r) // r est null initialement
      ⋮
  r = new List(i_n, r)
  …
(Et renvoie r.)
Donc la liste renvoyée est : [i_n; …; i₁].

Planche : 8

Retourner une liste

Il y a (au moins) deux façons d’aborder la question.

On peut procéder comme pour la lecture. Les entiers étant cette fois extraits de la liste à retourner.
static List rev(List p) {
   List r = null ;
   while (p != null) { // Tant qu'il y a des entiers...
     r = new List(p.val, r) ;
     p = p.next ;       // Les consommer
   }
   return r ;
}
Mieux : Boucle idiomatique.
  for (; p != null ; p = p.next) {
    r = new List(p.val, r) ;
  }

Planche : 9

Approche récursive

Généralisons le problème (comme souvent).

La methode revAppend(p₁ ; …; p_n, q₁ ; …; q_m) doit renvoyer la liste p_n; …; p₁; q₁ ; … q_m.

Par induction sur la première liste, la fonction R suivante convient.

R(∅, Q)	=	Q
R((a; P), Q)	=	R(P, (a;Q))

En notant P la liste P retournée, et par hypothèse de récurrence :

R(P, (a; Q)) =

; a ; Q

Avec a; P = P ; a (disons par définition du retournement).

Planche : 10

Programmation de R

Les équations :

R(∅, Q)	=	Q
R((a; P), Q)	=	R(P, (a;Q))

Le code :

static List revAppend(List p, List q) {
  if (p == null) {
    return q ;
  } else {
    return revAppend(p.next, new List(p.val, q)) ;
  }
}

static List rev(List p) {
  return revAppend(p, null) ;
}

Planche : 11

Élimination de la récursion (terminale)

La boucle,

  x = x₀ ; r = r₀ ;
  while (P(x)) {
    r = f(x, r) ;  x = g(x) ;
  }

Équivaut à la récursion

static … recLoop(… x, … r) {
  if (P(x)) {
     return recLoop(g(x), f(x, r)) ;
  } else {
     return r ;
  }
}
  … r = recLoop(x₀, r₀) …

Remarquer C’est un complément : aller voir le poly.

Planche : 12

Un autre exemple : l’affichage

C’est plus simple, car il n’y a pas de résultat (accumulateur r).

Récursif
  private static void doPrint(List p) {
    if (p != null) {
      System.out.println(p.val) ;
      doPrint(p.next) ;
    }
  }
  static print(List p) { doPrint(p) ; } ;
(afficher a ; P c’est afficher a, puis afficher P.)
Itératif
  static void print(List p) {
    for ( ; p != null ; p = p.next) {
      System.out.println(p.val) ;
    }}

Planche : 13

Encore un exemple : n-ième élement

Récursif

static int nth(int i, List p) {
  if (p == null) { throw new Error() ; }
  if (i == 0) {
    return p.val ;
  } else {
    return nth(i-1, p.next) ;
}

Itératif: allons nous pouvoir utiliser la boucle idiomatique ? Oui

static int nth(int i, List p) {
  for ( ; p != null ; p = p.next) {
    if (i == 0) return p.val ;
    i-- ;
  }
  throw new Error() ;
}

Planche : 14

À propos

On ne doit pas écrire :

  for (int i = 0 ; i < length(p) ; i++) {
    int x = nth(i, p) ;
    …
  }

Mais plutôt.

  for (List q = p ; q != null ; q = q.next) {
    int x = q.val ;
    …
  }

Pourquoi

Efficacité (quadratique/linéaire).
Mais surtout harmonie, le premier code convient aux tableau (accès dit aléatoire) le second aux listes (accès dit séquentiel).

Planche : 15

Que retenir ?

La programmation récursive est la plus puissante (et de loin).

Par exemple, afficher à l’envers.

  static void revPrint(List p) {
    if (p != null) {
      revPrint(p.next) ;
      System.out.println(p.val) ;
    }
  }

(afficher a ; P à l’envers, c’est afficher P à l’envers, puis afficher a.)

Pas de version itérative… simple.

Planche : 16

Pourquoi trier ?

On a parfois tout simplement besoin de trier.
- Le professeur trie les lignes d’une feuille de calcul (genre Excel), selon les noms des élèves, ou selon les notes obtenues à un examen, selon qu’il veut contrôler qu’aucun élève ne manque, ou classer les élèves.
Opérer sur des données triées, est parfois, plus simple, plus efficace, ou même plus simple et plus efficace.
- Par exemple, enlever les doublons d’une liste.
  - Sur une liste triée, il suffit d’un parcours, car les doublons se suivent.
  - Sur une liste non-triée, il faut multiplier les parcours.

Planche : 17

Trier une liste simplement

Trions une main à la belote (ou au bridge).

je prend les cartes dans la main gauche,
je prend une carte et la met dans ma main droite,
je prend une carte et la range à sa place dans ma main droite,
je prend une carte et la range à sa place dans ma main droite,
⋮
ma main gauche est vide.

L’insertion semble plus simple dans une liste que dans un tableau.

Planche : 18

Insertion, équations

Trouver la place où ranger la nouvelle valeur x dans une liste triée

static boolean ici(int x, List p) {
return (p == null || x <= p.val) ;
}

Noter : ici(x, P) faux entraîne P non-vide.

I(x, P)	=	x; P	,	si `ici`(x, P)
I(x, (a; P))	=	a ; I(x, P)	,	sinon

Correction :

Base : Si ici(x,P) et P triée, alors (x; P) est triée.
Induction : Sinon (liste a; P avec a < x)
- a minore P et x, et donc I(x, P).
- I(x, P) est trié (induction).

Planche : 19

Programmation du tri des listes

D’abord le tri en supposant insert écrite.

static List sort(List p) {
  List r = null ;
  for ( ; p != null ; p = p.next) {
    r = insert(p.val, r) ;
  }
  return r ;
}

Et l’insertion.

static List insert(int x, List p) {
  if (ici(x,p)) {
    return new List (x, p) ;
  } else { // (p != null) && (x > p.val)
    return new List (p.val, insert(x, p.next)) ;
  }
}

Planche : 20

Combien ça coûte

Pour une liste de taille (longeur) n.

La méthode sort appelle n fois insert,
En outre, elle est responsable de moins de k₁ × n + k₀ autres opérations (élémentaires, i.e. de coût constant).
Chacun de ces n appels de insert(x,p) (p de longeur ℓ) se solde par moins de k′₁ × ℓ + k′₀ opérations.
ℓ vaut 0, 1, …n−1.
Au final le tri s’effectue en moins de
k₁ × n + k₀ + n × (k′₁ × n + k′₀)

Soit un coût en O(n²).

La borne O(n²) est bien serrée (listes triées de tailles croissante).

Planche : 21

Combien ça coûte ? II

On peut (plus simplement) compter les comparaisons.

n−1 ≤ I(n) ≤

n (n−1)

Ici, I(n) est le nombre de comparaisons d’éléments effectuées pour trier une liste de taille n.

Ce résultat donne une indication sensée du temps d’exécution.

La comparaison est souvent l’opération la plus coûteuse (tri de grandes chaînes).
On peut affecter un nombre constant d’opérations à chaque comparaison (la borne asymptotique est inchangée).

On peut aussi compter le nombre de cellules de listes allouées.

n ≤ I(n) ≤

n (n+1)

Planche : 22

Coût en moyenne

Les arguments du tri sont pris dans un espace de probabilité (S). On calcule l’espérance de la variable aléatoire « coût » (X).

E(X) =

∑

s ∈ S

p_s X

Ici, avec la loi uniforme sur les permutations de n éléments

n ≤ Î(n) ≤

n (n−1)

Plus précisément, pour les permutations de n éléments distincts (voir le poly).

Î(n) =

n² +

n − lnn + O(1)

Planche : 23

Insertion « en place »

La méthode insert précedente n’est pas conforme à l’intuition d’insertion dans un jeu de cartes.

Revenons aux equations

I(x, P)	=	x; P	,	si `ici`(x, P)
I(x, (a; P))	=	a ; I(x, P)	,	sinon

Et interprétons les ainsi,

Si ici(x, P), alors ajouter en tête

Sinon, insérer x dans P.next

Par le premier « Si… », la méthode I doit renvoyer une liste. Soit finalement :

Si ici(x, P), alors renvoyer x ; P

Sinon, changer P.next en I(x,P.next) et renvoyer P.

Planche : 24

Programmation de l’insertion en place

En bref,

static List insert(int x, List p) {
  if (ici(x, p)) { // Ajouter en tête
    return new List (x, p) ;
  } else {         // Insérer dans p.next
    p.next = insert(x, p.next) ;
    return p ;
  }
}

Question : Changer le contenu d’une cellule pose-t-il un problème ? non !

Pourquoi ? Il n’y a aucun partage possible des cellules de la liste triée, dont toutes les cellules sont créées par insert (sont nouvelles)

Planche : 25

Insertion en place, itérative

Dans la solution récursive, au plus une seule des affections est utile.

On peut l’éviter ainsi :

static List insert(int x, List p) {
  // Cas particulier : insertion en tête.
  if (ici(x,p)) return new List(x, p) ;
  // Cas général, insertion après une cellule.
  List q = p, prev ;
  do {
     prev = q ; q = q.next ;
     // prev est la cellule qui précède q
  } while (!ici(x,q)) ;
  prev.next = new List(x, q) ;
  return p ;
}

Au fond, c’est exagéré.

Planche : 26

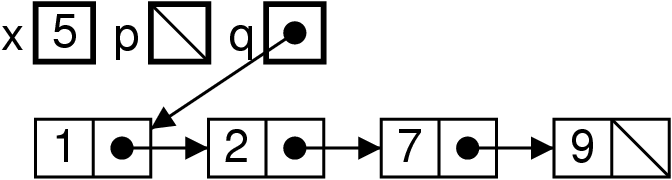
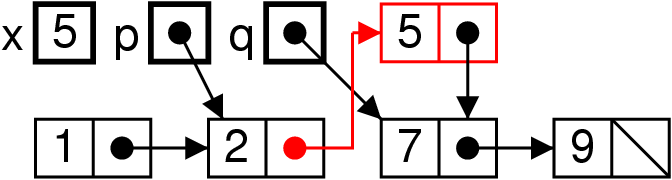
Fonctionnement, vision itérative

Commencer

Trouver la place (sortie itération)

Planche : 27

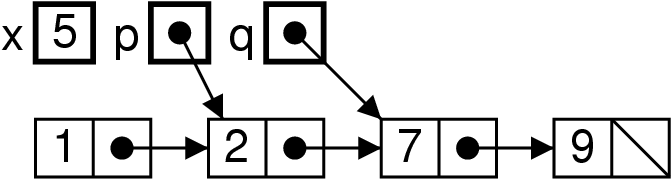
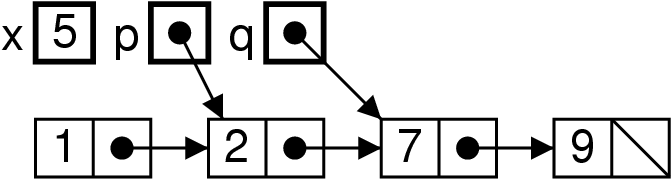
Insérer

Exécuter

prev.next = new List (5, q) ;

Planche : 28

Deux styles de structures de données

Style persistant ou fonctionnel. C’est à dire : on affecte jamais les champs des objets (mais on les initialise).
- Plus sûr.
- Alloue plus de mémoire (la performance dépend alors crucialement de l’efficacité de l’environnement d’exécution).
Style destructif, ou mutable, ou non-persistant.
- En cas de partage non maîtrisé, les résultats sont surprenants.
- En cas de partage absent, ou maîtrisé, peut être intéressant.

Planche : 29

Deux styles de programmation

Récursif
- Souvent plus simple à programmer.
Itératif
- Toujours plus efficace (en Java), mais dans une mesure difficile à estimer à l’avance.

Planche : 30

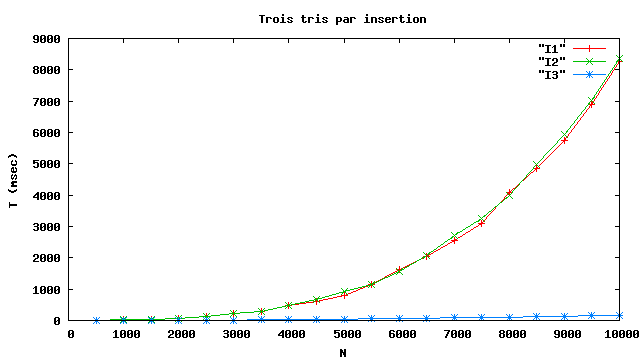
Comparaison des trois versions

I1 et I2 semblent bien en O(n²).
I3 (destructif, itératif) est bien plus rapide.

Planche : 31

Changement d’échelle

I3 (destructif, itératif) semble bien en O(n²).

Planche : 32

La bonne réaction

Si un programme est trop lent…

Y a-t-il un algorithme plus efficace ?

Pour le tri…

Il y a des algorithmes en O(n logn).

Fusion des listes triées

Par définition :

La fusion de deux listes triées est une liste triée qui regroupe les éléments des deux listes fusionnées.

Planche : 33

Fusion correcte

Soit M(X,Y) la fusion (M pour merge).

Équations :

M(∅, Y)	=	Y
M(X, ∅)	=	X
M((x; X), (y; Y))	=	x; M(X, (y; Y))	si x ≤ y
M((x; X), (y; Y))	=	y; M((x ; X), Y)	si y ≤ x

Correction : (du troisième cas)

x minore X (hyp.) et y ; Y (x ≤ y et hyp.).
En outre, M(A, B) regroupe les éléments de A et B.
Et donc x minore M(X, (y; Y)).
Par ailleurs, M((x; X), (y; Y)) regroupe les éléments de (x; X) et (y; Y).

Planche : 34

Code de la fusion

static List merge(List xs, List ys) {
  if (xs == null) {
    return ys ;
  } else if (ys == null) {
    return xs ;
  } // NB: désormais xs != null && ys != null
    else if (xs.val <= ys.val) {
    return new List (xs.val, merge(xs.next, ys)) ;
  } else { // NB: ys.val < xs.val
    return new List (ys.val, merge(xs, ys.next)) ;
  }
}

Coût de la fusion

Si M(n₁, n₂) représente le nombre de comparaisons d’éléments.

min(n₁, n₂) ≤ M(n₁, n₂) ≤ n₁ + n₂

Planche : 35

Principe du tri fusion

Exemple de la classique méthode « divide and conquer ».

Diviser L en L₁ et L₂.
Trier L₁ et L₂ independamment (récursion).
Fusionner L₁ et L₂.

Note : Comment garantir la terminaison ?

Il faut L₁ et L₂ de taille strictement inférieure à L,
et donc L de longueur ≥ 2.

Planche : 36

Tri fusion, diviser

En un parcours de liste : séparer les pairs des impairs.

static List mergeSort(List xs) {
  List ys = null, zs = null ;
  boolean even = true ; // zéro est pair
  for (List p = xs ; p != null ; p = p.next ) {
    if (even) {
      ys = new List (p.val, ys) ;
    } else {
      zs = new List (p.val, zs) ;
    }
    even = !even ; // k+1 a la parité opposée à celle de k
  }
  ⋮

Planche : 37

Tri fusion, conquérir

  ⋮
  if (zs == null) { // xs a zéro ou un élément
    return xs ; // et alors xs est triée
  } else { // Les longueurs de ys et sz sont < à la longueur de xs
    return merge(mergeSort(ys), mergeSort(zs)) ;
  }
}

Coût à la louche :

Une fusion → n, soit (au pire) n comparaisons.
Deux fusions → n/2, soit (au pire) n comparaisons.
Quatre fusions → n/4, soit (au pire) n comparaisons.
Etc.

Etc. veut dire environ log₂(n) fois. Au final : O(n log n).

Planche : 38

Plus précisément

Équations du coût (nombre de comparaisons).

S(0) = 0

S(1) = 0

S(n) = M(

⎡

n/2

⎤

⎣

n/2

⎦

) + S(

⎡

n/2

⎤

) + S(

⎣

n/2

⎦

), pour n > 1

Soit (encadrer le coût de la fusion).

⎣

n/2

⎦

+ S(

⎡

n/2

⎤

) + S(

⎣

n/2

⎦

) ≤ S(n) ≤ n + S(

⎡

n/2

⎤

) + S(

⎣

n/2

⎦

)

Si n = 2^p+1 on a la simplification très nette

2^p + 2·S(2^p) ≤ S(2^p+1) ≤ 2^p+1 + 2·S(2^p)

Et donc (diviser par 2^p+1, recurrence T(p+1) = k + T(p)).

1/2·p·2^p ≤ S(2^p) ≤ p·2^p

Planche : 39

Et donc, finalement

En fait, on peut généraliser (voir le poly).

1/2·log₂(n/2)·n/2 ≤ S(n) ≤ log₂(2n)·2n

Soit :

S(n)	=	Θ(n · log n)
Ŝ(n)	=	Θ(n · log n)

Le point important Quelque soit la liste, le tri effectue toujours de l’ordre de n log n comparaisons.

Planche : 40

Vérifions l’efficacité

I est le tri par insertion le plus efficace. L’accélération est impressionante.

Planche : 41

Passer aux grandes listes

On tente de trier des liste de taille k × 10000.

N=10000 T=37
N=20000 T=249
N=30000 T=238
Exception in thread "main" java.lang.StackOverflowError
        at List.merge(T.java:148)
        at List.merge(T.java:148)
        at List.merge(T.java:148)
  ⋮

J’ai effacé de l’ordre de 200 lignes d’appels de méthodes en attente.

En pratique, le nombre d’appels de méthode qui attendent le résultat d’un appel de méthode est limité.

Or merge appelle merge qui appelle merge qui…

Planche : 42

Quelle solution ?

Dire à Java d’accepter plus d’appels de méthode en attente.
Solution partielle, et comment faire ?
Programmer différemment
Solution définitive.

Différemment veut dire sans appel récursif : programmer une fusion itérative (cf. poly 1.3.3).

Planche : 43

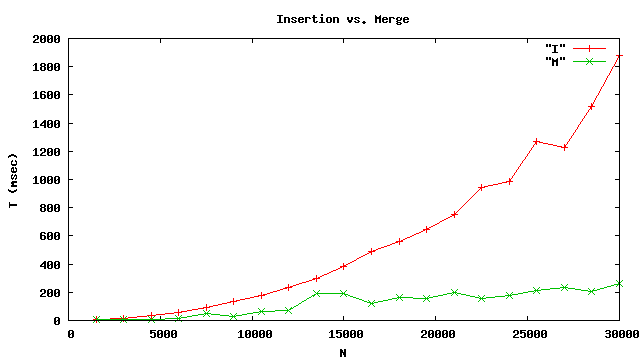
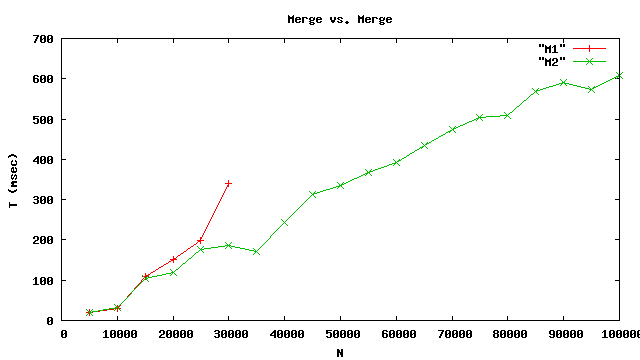
Performances

Noter : La courbe M1 est incomplète, en raison de l’échec. Ici programmer itérativement n’est pas une question d’efficacité, mais une nécessité (si on veut trier de grandes listes).

Planche : 44

Diversion: static, pas static ?

Slogan :

static ∼ La classe, Pas static ∼ L’objet.

Je veux la représentation décimale de l’entier x dans la chaîne s.

Avec méthode statique.
String s = Integer.toString(x) ; // Appeler une fonction.
Avec méthode (dynamique, pas statique).
Integer ox = new Integer (x) ; // Fabriquer un objet.
String s = ox.toString() ; // Et invoquer sa méthode.

Planche : 45

Diversion II: static, pas static ?

Je code la méthode, à partir de la méthode statique.
class Integer {
  private int x ; // Champ privé
  Integer (int x) { this.x = x ; }
  static String toString(int z) { … }

  String toString() { return toString(this.x) ; }
}
Je code la méthode statique, à partir de la méthode.
  String toString() { … }

  static String toString(int x)
    { return new Integer(x).toString() ; }

Planche : 46

Et la programmation objet ?

La programmation des listes vues comme telles, n’a rien d’une programmation « style objet ».

Pire, il serait absurde de s’imposer ce style ici.

Mais qu’est-ce que le style objet ?

Exemple, on veut des objets d’une classe Set, qui offrent :

Une méthode add(int x) pour ajouter un élément.
Etc.

Par exemple, on ajoute l’élément x à l’ensemble s par

s.add(x)

Important : Le style objet n’abolit pas la distinction persistant/impératif. Au contraire il permet de la rendre visible.

Planche : 47

Ensembles persistants

Ajouter un ou des éléments renvoie un nouvel ensemble.

class Set {
  Set () // Construire un ensemble vide
  Set add(int x) // Ajouter l'élément x.
  public String toString() // Comme d'habitude.
}

Usage :

  Set s0 = new Set () ;
  Set s1 = s0.add(3) ;
  Set s2 = s1.add(1) ;
  Set s3 = s2.add(2) ;

Important : L’ensemble vide n’est pas null.

Planche : 48

Ensembles impératifs

Ajouter un ou des éléments modifie l’ensemble.

class ISet {
  ISet () // Construire un ensemble vide
  void add(int x) // Ajouter l'élément x.
  public String toString() // Comme d'habitude.
}

Usage :

  ISet s0 = new ISet () ;
  s0.add(3) ;
  s0.add(1) ;
  s0.add(2) ;

Important : Les méthodes ne renvoient rien (void). C’est la bonne façon de procéder.

Planche : 49

Implémentation I

On décide de représenter les ensembles par des listes triées.

Écrivons une méthode pour ajouter un élément dans un ensemble représenté par une liste triée.

// Comme insert, éviter les doublons.
static List add(int x, List xs) {
   if (xs == null) { // Ajouter ici
     return new List(x, xs) ;
   } else if (x < xs.val) { // Ajouter ici aussi
     return new List(x, xs) ;
   else if (x > xs.val) { // Ajouter plus loin
     return new List(xs.val, add(x, xs.next)) ;
   } else { // x == xs.val, déjà là
     return xs ;
   }
}

Dans la classe List, évidemment.

Planche : 50

Effet mémoire

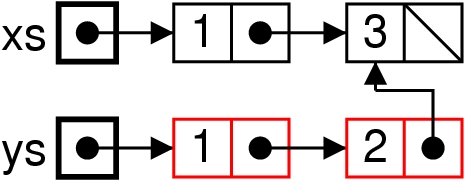
List xs = new List(1, new List(3, null)) ;
List ys = List.add(2, xs) ;

Planche : 51

Implémentation II

La méthode List.add fait le vrai travail, reste à « encapsuler ».

class Set {
  private List elts ; // Liste des eléments, usage interne.

  Set () { elts = null ; } // Inutile, marque l'intention.
  private Set (List elts) { this.elts = elts ; } // Usage interne.

  Set add(int x) { return new Set (List.add(x, this.elts)) ; }
}

class ISet {
  private List elts ; // Liste des eléments, usage interne.

  ISet () { elts = null ; } // Inutile, marque l'intention.

  void add(int x) { this.elts = List.add(x, elts) ; }
}

Planche : 52

Avec des listes non-persistantes

Le code de nadd se déduit facilement de celui de add.

static List nadd(int x, List xs) {
   if (xs == null || x < xs.val) { // Ajouter ici
     return new List(x, xs) ;
   else if (x > xs.val) { // Ajouter plus loin
     xs.next = nadd(x, xs.next) ;
     return xs ;
   } else { // x == xs.val, déjà là
     return xs ;
   }
}

Noter que nadd ne peut pas renvoyer void, à cause du cas de l’élément ajouté en tête.

Planche : 53

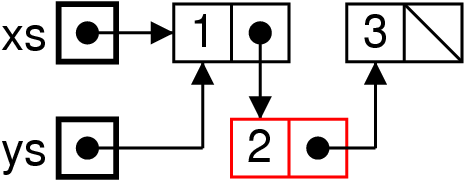
Effet mémoire

List xs = new List(1, new List(3, null)) ;
List ys = List.nadd(2, xs) ; // Pas très malin

En effet la liste pointée par xs a changé !

On peut sans doute se contraindre à écrire.

xs = List.nadd(2, xs) ; // Bien plus logique

Mais rien n’est contrôlé par Java.

Planche : 54

Ensemble impératif, implémenté impérativement

Dans la classe ISet.

   void add(int x) {
     this.elts = List.nadd(x, this.elts) ;
   }

Et grâce à la signature de la méthode void add(..), l’utilisateur ne peut pas se tromper : il n’y a qu’un seul ensemble, qui est modifié au cours de sa vie.

L’encapsulage de la structure de donnée non-persistante augmente la sûreté de la programmation.

ISet s0 = new ISet () ; s0.add(3) ; s0.add(1) ; s0.add(2) ;
ISet s1 = s0 ;

s0.add(4) ; // Il semble « logique » que s1 change aussi.

Ce document a été traduit de L^AT_EX par H^EV^EA