Chapitre 6 Analyse Syntaxique
Un compilateur transforme un programme écrit en langage évolué en
une suite d'instructions élémentaires exécutables par une machine.
La construction de compilateurs a longtemps été considérée comme
une des activités fondamentale en programmation, elle a suscité le
développement de très nombreuses techniques qui ont aussi donné
lieu à des théories maintenant classiques. La compilation d'un
programme est réalisée en trois phases, la première (analyse
lexicale) consiste à découper le programme en petites entités:
opérateurs, mots réservés, variables, constantes numériques,
alphabétiques, etc. La deuxième phase (analyse syntaxique) consiste
à expliciter la structure du programme sous forme d'un arbre, appelé
arbre de syntaxe, chaque noeud de cet arbre correspond à un
opérateur et ses fils aux opérandes sur lesquels il agit. La
troisième phase (génération de code) construit la suite
d'instructions du micro-processeur à partir de l'arbre de syntaxe.
Nous nous limitons dans ce chapitre à l'étude de l'analyse
syntaxique. L'étude de la génération de code, qui est la partie la
plus importante de la compilation, nous conduirait à des
développements trop longs. En revanche, le choix aurait pu se porter
sur l'analyse lexicale, et nous aurait fait introduire la notion
d'automate. Nous préférons illustrer la notion d'arbre, étudiée au
chapitre 4, et montrer des exemples d'arbres représentant une formule
symbolique. La structure d'arbre est fondamentale en informatique.
Elle permet de représenter de façon structurée et très efficace
des notions qui se présentent sous forme d'une chaîne de
caractères. Ainsi, l'analyse syntaxique fait partie des nombreuses
situations où l'on transforme une entité, qui se présente sous une
forme plate et difficile à manipuler, en une forme structurée
adaptée à un traitement efficace. Le calcul symbolique ou formel, le
traitement automatique du langage naturel constituent d'autres
exemples de cette importante problématique. Notre but n'est pas de
donner ici toutes les techniques permettant d'écrire un analyseur
syntaxique, mais de suggérer à l'aide d'exemples simples comment il
faudrait faire. L'ouvrage de base pour l'étude de la compilation est
celui de A. Aho, R. Sethi, J. Ullman [3]. Les premiers
chapitres de l'ouvrage [33] constituent une
intéressante introduction à divers aspect de l'informatique
théorique qui doivent leur développement à des problèmes
rencontrés en compilation.
6.1 Définitions et notations
6.1.1 Mots
Un programme peut être considéré comme une très longue chaîne de
caractères, dont chaque élément est un des
symboles le composant. Un minimum de terminologie sur les
chaînes de caractères ou mots est nécessaire pour décrire
les algorithmes d'analyse syntaxique. Pour plus de précisions sur
les propriétés algébriques et combinatoires des
mots, on pourra se reporter à [34].
On utilise un ensemble fini appelé alphabet A dont les
éléments sont appelés des lettres. Un mot est une
suite finie f = a1 a2 ... an de lettres, l'entier n
s'appelle sa longueur. On note par e le mot vide, c'est le
seul mot de longueur 0. Le produit de deux mots f et g est
obtenu en écrivant f puis g à la suite, celui ci est noté fg.
On peut noter que la longueur de fg est égale à la somme des
longueurs de f et de g. En général fg est différent de gf.
Un mot f est un facteur de g s'il existe deux mots g' et
g'' tels que g = g' f g'', f est facteur gauche de g si
g = fg'' c'est un facteur droit si g = g'f. L'ensemble des
mots sur l'alphabet A est noté A*.
Exemples
- Mots sans carré
Soit l'alphabet A = {a, b,c }. On construit la suite de mots
suivante f0 = a, pour n ³ 0, on obtient récursivement
fn+1 à partir de fn en remplaçant a par abc, b par
ac et c par b. Ainsi:
f1 = abc f2 = abcacb f3 = abcacbabcbac
Il est assez facile de voir que fn est un facteur gauche de
fn+1 pour n ³ 0, et que la longueur de fn est 3 ×
2n-1 pour n ³ 1. On peut aussi montrer que pour tout n,
aucun facteur de fn n'est un carré, c'est à dire que
si gg est un facteur de fn alors g = e. On peut noter à
ce propos que, si A est un alphabet composé des deux lettres a et
b, les seuls mots sans carré sont a,b,ab,ba,aba,bab. La
construction ci-dessus, montre l'existence de mots sans carré de
longueur arbitrairement grande sur un alphabet de trois lettres.
- Expressions préfixées
Les expressions préfixées, considérées au
chapitre 3 peuvent être transformées en des mots sur l'alphabet
A = {+, *, (, ), a },
on remplace tous les nombres par la lettre a pour en simplifier
l'écriture. En voici deux exemples,
f = (* a a) g = ( * ( + a (* a a)) (+ (* a a) (* a a)))
- Un exemple proche de la compilation
Considérons l'alphabet A suivant, où les ``lettres'' sont des mots sur
un autre alphabet:
A = {begin, end, if, then, else,
while, do, ;, p, q, x,
y, z }
Alors f = while p do begin if q then x else y ; z end
est un mot de longueur 13, qui peut se décomposer en
f = while p do begin g ; z end
où g = if q then x else y.
6.1.2 Grammaires
Pour construire des ensembles de mots, on utilise la notion de grammaire. Une grammaire G comporte deux alphabets A et
X, un axiome S 0 qui est une lettre appartenant à X
et un ensemble R de règles.
- L'alphabet A est dit alphabet terminal, tous les mots
construits par la grammaire sont constitués de lettres de A.
- L'alphabet X est dit alphabet auxiliaire, ses lettres
servent de variables intermédiaires servant à engendrer des mots.
Une lettre S0 de X, appelée axiome, joue un rôle particulier.
- Les règles sont toutes de la forme:
S ® u
où S est une lettre de X et u un mot comportant des lettres
dans A È X.
Exemple
A = {a, b }, X = {S, T, U },
l'axiome est S .
Les règles sont données par :
| S ® aT bS | | S ® bU aS | | S ® e |
| T ® aT bT | | T ® e | | |
| U ® bU aU | | U ® e | | | |
|
Pour engendrer des mots à l'aide d'une grammaire, on
applique le procédé suivant:
On part de l'axiome S0 et on choisit une règle de la forme S0
® u. Si u ne contient aucune lettre auxiliaire, on a terminé.
Sinon, on écrit u = u1Tu2. On choisit une règle de la forme T
® v. On remplace u par u' = u1vu2. On répète l'opération
sur u' et ainsi de suite jusqu'à obtenir un mot qui ne contient que
des lettres de A.
Dans la mesure où il y a plusieurs choix possibles à
chaque étape on voit que le nombre de mots engendrés par une
grammaire est souvent infini. Mais certaines grammaires peuvent
n'engendrer aucun mot. C'est le cas par exemple des grammaires dans
lesquelles tous les membres droits des règles contiennent un lettre
de X.
On peut formaliser le procédé qui engendre les mots d'une
grammaire de façon un peu plus précise en définissant la notion
de dérivation. Etant donnés deux mots u et v contenant
des lettres de A È X, on dit que u dérive
directement de v pour la grammaire G, et on note v ® u,
s'il existe deux mots w1 et w2 et une règle de grammaire S
® w de G tels que v = w1S w2 et u = w1ww2. On dit
aussi que v se dérive directement en u.
On dit que u dérive de v, ou que v se dérive
en u, si u s'obtient à partir de v par une suite finie de
dérivations directes. On note alors:
Ce qui signifie l'existence de w0, w1, ... wn,
n ³ 0 tels que w0 = v, wn = u et pour tout i = 1, ...
n, on a wi-1® wi.
Un mot est engendré par une grammaire G, s'il dérive de
l'axiome et ne contient que des lettres de A, l'ensemble de tous les
mots engendrés par la grammaire G, est le langage
engendré par G; il est noté L(G).
Exemple
Reprenons l'exemple de grammaire G donné plus haut et
effectuons quelques dérivations en partant de S. Choisissons S
® aTbS, puis appliquons la règle T ® e. On obtient:
S ® aTbS ® abS
On choisit alors d'appliquer S ® b UaS . Puis, en
poursuivant, on construit la suite
S ® aTbS ® abS ® abbUaS ® abbbUaUaS ® abbbaUaS
® abbbaaS ® abbbaa
D'autres exemples de mots L (G) sont bbaa
et abbaba que l'on obtient à l'aide de calculs similaires:
S ® bU aS ® bbU aU aS ® bbaU aS
® bbaaS ® bbaa
S ® aT bS ® abS ® abbUaS
® abbaS ® abbabU aS ® abbabaS
® abbaba
Plus généralement, on peut montrer que, pour cet exemple,
L (G) est constitué de tous les mots qui contiennent
autant de lettres a que de lettres b.
Notations
Dans la suite, on adoptera des conventions strictes de notations, ceci
facilitera la lecture du chapitre. Les éléments de A sont notés
par des lettres minuscules du début de l'alphabet a, b, c, ...
éventuellement indexées si nécessaire a1, a2, b1, b2 ...,
ou bien des symboles appartenant à des langages de programmation.
Les éléments de X sont choisis parmi les lettres majuscules S,
T, U par exemple. Enfin les mots de A* sont notés par f, g, h
et ceux de (A È X)* par u, v, w, indexés si besoin est.
6.2 Exemples de Grammaires
6.2.1 Les systèmes de parenthèses
Le langage des systèmes de parenthèses joue un rôle important tant
du point de vue de la théorie des langages que de la programmation.
Dans les langages à structure de blocs, les begin end
ou les { } se comportent comme des parenthèses ouvrantes
et fermantes. Dans des langages comme Lisp, le décompte correct des
parenthèses fait partie de l'habileté du programmeur. Dans ce qui
suit, pour simplifier l'écriture, on note a une parenthèse
ouvrante et b une parenthèse fermante. Un mot de {a, b}* est
un système de parenthèses s'il contient autant de a que de b et
si tous ses facteurs gauches contiennent un nombre de a supérieur
ou égal au nombre de b. Une autre définition possible est
récursive, un système de parenthèses f est ou bien le mot vide (f = e) ou bien formé par deux systèmes de parenthèses
f1 et f2 encadrés par a et b (f = af1bf2). Cette
nouvelle définition se traduit immédiatement sous la forme de
la grammaire suivante:
A = {a, b }, X = {S }, l'axiome est S et les règles sont
données par:
S ® aS bS S ® e
On notera la simplicité de cette grammaire, la définition
récursive rappelle celle des arbres binaires, un tel arbre est
construit à partir de deux autres comme un système de parenthèses
f l'est à partir de f1 et f2.
La grammaire précédente a la particularité, qui est parfois un
inconvénient, de contenir une règle dont le membre droit est le mot
vide. On peut alors utiliser une autre grammaire déduite de la
première qui engendre l'ensemble des systèmes de parenthèses non
réduits au mot vide, dont les règles sont:
| S ® aSbS | | S ® aSb | | S ® abS | | S ® ab
| |
|
Cette transformation peut se généraliser et on peut ainsi
pour toute grammaire G trouver une grammaire qui engendre le
même langage, au mot vide près, et qui ne contient pas de règle de
la forme S ® e.
6.2.2 Les expressions arithmétiques préfixées
Ces expressions ont été définies dans le chapitre 3 et la structure
de pile a été utilisée pour leur évaluation. Là encore, la
définition récursive se traduit immédiatement par une grammaire:
A = {+, *, (, ), a }, X = {S }, l'axiome est S, les
règles sont données par:
S ® (+ S S )
S ® (* S S)
S ® a
Les mots donnés en exemple plus haut sont
engendrés de la façon suivante:
S ® (T S S ) ®* (* a a)
S ® (T S S ) ®*
( T (T S S ) (T S S )) ®*
( T (T S (T S S )) (T (T S S ) (T S S )))
®*
( * ( + a (* a a)) (+ (* a a) (* a a)))
Cette grammaire peut être généralisée pour traiter des
expressions faisant intervenir d'autres opérateurs d'arité
quelconque. Ainsi, pour ajouter les symboles Ö ,
- et /. Il suffit de considérer deux nouveaux éléments T1 et
T2 dans X et prendre comme nouvelles règles:
| S ® (T1 S ) | | S ® (T2 S S ) | | S ® a | | | | | | |
| T1 ® Ö | | T1 ® - | | T2 ® + | | T2 ® * | | T2 ® - | | T2 ® /
|
On peut aussi augmenter la grammaire de façon à
engendrer les nombres en notation décimale, la lettre a devrait
alors être remplacée par un élément U de X et des règles
sont ajoutées pour que U engendre une suite de chiffres ne
débutant pas par un 0.
| U ® V1 U1 | | U ® V | | U1 ® V U1 | | U1 ® V |
|
V1 ® i pour 1 £ i £ 9
|
| V ® 0 | | V ® V1 | | | |
6.2.3 Les expressions arithmétiques
C'est un des langages que l'on choisit souvent comme exemple en
analyse syntaxique, car il contient la plupart des difficultés
d'analyse que l'on rencontre dans les langages de programmation. Les
mots engendrés par la grammaire suivante sont toutes les expressions
arithmétiques que l'on peut écrire avec les opérateurs + et *
on les appelle parfois expressions arithmétiques infixes. On les
interprète en disant que * est prioritaire vis à vis de +.
A = {+, *, (, ), a }, X = {E, T, F},
l'axiome est E,
les règles de grammaire sont données par:
| E ® T | | T ® F | | F ® a |
| E ® E + T | | T ® T * F | | F ® (E)
| |
|
Un mot engendré par cette grammaire est par exemple:
(a + a*a) * (a *a + a*a )
Il représente l'expression
(5 + 2*3) * (10*10 + 9*9)
dans laquelle tous les nombres ont été remplacés par le
symbole a.
Les lettres de l'alphabet auxiliaire ont été choisies pour
rappeler la signification sémantique des mots qu'elles
engendrent. Ainsi E, T et F représentent respectivement les
expressions, termes et facteurs. Dans cette terminologie, on constate
que toute expression est somme de termes et que tout terme est produit
de facteurs. Chaque facteur est ou bien réduit à la variable a ou
bien formé d'une expression entourée de parenthèses. Ceci traduit
les dérivations suivantes de la grammaire.
| E ® E + T ® E + T + T ... ...
|
| T+T+T ... +T |
| T ® T * F
® T * F * F ... ...
|
| F*F*F ... *F |
La convention usuelle de priorité de l'opération * sur
l'opération + explique que l'on commence par engendrer des sommes
de termes avant de décomposer les termes en produits de facteurs, en
règle générale pour des opérateurs de priorités quelconques on
commence par engendrer les symboles d'opérations ayant la plus faible
priorité pour terminer par ceux correspondant aux plus fortes.
On peut généraliser la grammaire pour faire intervenir
beaucoup plus d'opérateurs. Il suffit d'introduire de nouvelles
règles comme par exemple
E ® E - T T ® T / F
si l'on souhaite introduire des soustractions et des divisions. Comme
ces deux opérateurs ont la même priorité que l'addition et la
multiplication respectivement, il n'a pas été nécessaire
d'introduire de nouveaux éléments dans X. Il faudrait faire
intervenir de nouvelles variables auxiliaires si l'on introduit de
nouvelles priorités.
La grammaire donnée ci-dessous engendre aussi le langage
des expressions infixes. On verra que cette dernière permet de faire
plus facilement l'analyse syntaxique. Elle n'est pas utilisée en
général en raison de questions liées à la non-associativité de
certains opérateurs comme par exemple la soustraction et la division.
Ceci pose des problèmes lorsqu'on désire généraliser la grammaire
et utiliser le résultat de l'analyse syntaxique pour effectuer la
génération d'instructions machine.
| E ® T | | T ® F | | F ® a |
| E ® T + E | | T ® F * T | | F ® (E)
| |
|
6.2.4 Grammaires sous forme BNF
La grammaire d'un langage de programmation est très souvent
présentée sous la forme dite grammaire BNF qui n'est autre qu'une
version très légèrement différente de notre précédente notation.
Dans la convention d'écriture adoptée pour la forme BNF, les éléments
de X sont des suites de lettres et symboles comme MultiplicativeExpression, UnaryExpression. Les règles ayant le
même élément dans leur partie gauche sont regroupées et cet élément
n'est pas répété pour chacune d'entre elles. Le symbole ® est
remplacé par : suivi d'un passage à la ligne. Quelques
conventions particulières permettent de raccourcir l'écriture, ainsi
one of permet d'écrire plusieurs règles sur la même ligne.
Enfin, les éléments de l'alphabet terminal A sont les mots-clé,
comme class, if, then, else, for,
..., et les opérateurs ou séparateurs comme + * / - ; , ( )
[ ] = == < > .
Dans les grammaires données en annexe, on compte dans la grammaire de
Java 131 lettres pour l'alphabet auxiliaire et 251 règles. Il est hors
de question de traiter ici de cet exemple trop long. Nous nous
limitons aux exemples donnés plus haut dans lesquels figurent déjà
toutes les difficultés que l'on peut trouver par ailleurs.
Notons toutefois que l'on trouve la grammaire des expressions
arithmétiques sous forme BNF dans l'exemple de la grammaire de Java
donnée en annexe. On trouve en effet à l'intérieur de cette
grammaire:
AdditiveExpression:
MultiplicativeExpression
AdditiveExpression + MultiplicativeExpression
AdditiveExpression - MultiplicativeExpression
MultiplicativeExpression:
UnaryExpression
MultiplicativeExpression * UnaryExpression
MultiplicativeExpression / UnaryExpression
MultiplicativeExpression
UnaryExpression:
PreIncrementExpression
PreDecrementExpression
+ UnaryExpression
- UnaryExpression
UnaryExpressionNotPlusMinus
UnaryExpressionNotPlusMinus:
PostfixExpression
UnaryExpression
! UnaryExpression
CastExpression
PostfixExpression:
Primary
Name
PostIncrementExpression
PostDecrementExpression
Primary:
PrimaryNoNewArray
ArrayCreationExpression
PrimaryNoNewArray:
Literal
this
( Expression )
ClassInstanceCreationExpression
FieldAccess
MethodInvocation
ArrayAccess
Ceci correspond approximativement dans notre notation à
| E ® M | | E ® E + M | | E ® E - M | | |
| M ® U | | M ® P * U | | M ® M / U | | M ® M % U |
| U ® I | | U ® D | | | | |
U ® + U | | U ® -U | | U ® U' | | |
| U' ® P' | | U' ® ~ U | | U' ® ! U | | U' ® C |
| P ® P' | | P ® N | | P ® I' | | P ® D' |
| P' ® P'' | | P' ® A | | | | |
| P'' ® L | | P'' ® this | | P'' ® ( E ) | | ...
|
6.3 Arbres de dérivation et arbres de syntaxe abstraite
Le but de l'analyse syntaxique est d'abord déterminer si un mot appartient
ou non au langage engendré par une grammaire. Il s'agit donc, étant
donné un mot f de construire la suite des dérivations qui a permis
de l'engendrer. Si l'on pratique ceci à la main pour de petits
exemples on peut utiliser la technique classique dite
``essais-erreurs'' consistant à tenter de deviner à partir d'un mot
la suite des dérivations qui ont permis de l'engendrer. Cette suite
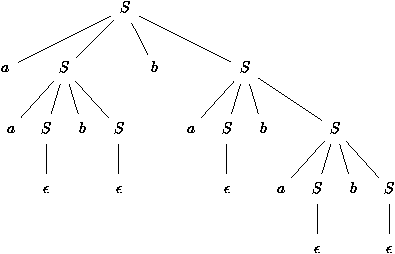
se présente bien plus clairement sous forme d'un arbre, dit arbre de dérivation dont des exemples sont donnés figures
6.1 et 6.2. Il s'agit de ceux obtenus pour les
mots aabbabab et (a + a*a) * (a*a + a*a) engendrés respectivement
par la grammaire des systèmes de parenthèses et par celle des
expressions infixes. On verra que ces arbres, ou plutôt une version
plus compact de ceux-ci, jouent un rôle
important pour la phase suivante de la compilation.
Une définition rigoureuse et complète des arbres de
dérivation serait longue, contentons nous de quelques indications
informelles. Dans un tel arbre, les noeuds internes sont étiquetés
par des lettres auxiliaires (appartenant à X) les feuilles par
des lettres de l'alphabet terminal. L'étiquette de la racine est
égale à l'axiome. Pour un noeud interne d' étiquette S, le mot
u obtenu en lisant de gauche à droite les étiquettes de ses fils
est tel que S ® u est une règle. Enfin, le mot f dont on fait
l'analyse est constitué des étiquettes des feuilles lues de gauche
à droite.
Pour un mot donné du langage engendré par une grammaire,
l'arbre de dérivation n'est pas nécessairement unique. L'existence
de plusieurs arbres de dérivations pour un même programme signifie
en général qu'il existe plusieurs interprétations possibles pour
celui ci. On dit que la grammaire est ambiguë, c'est le cas pour
l'imbrication des if then et if then else en Pascal. Des
indications supplémentaires dans le manuel de référence du langage
permettent alors de lever l'ambiguïté et d'associer un arbre unique
à tout programme Pascal. Ceci permet de donner alors une
interprétation unique. Toutes les grammaires données plus haut sont
non-ambiguës, ceci peut se démontrer rigoureusement, toutefois les
preuves sont souvent techniques et ne présentent pas beaucoup
d'intérêt.
Figure 6.1 : Arbre de dérivation de aabbabab
Figure 6.2 : Arbre de dérivation d'une expression arithmétique
L'arbre de dérivation est parfois appelé arbre de syntaxe
concrète pour le distinguer de l'arbre de syntaxe abstraite
construit généralement par le compilateur d'un langage de
programmation. Cet arbre de syntaxe abstraite est plus compact que le
précédent et contient des informations sur la suite des actions
effectuées par un programme. Chaque noeud interne de cet arbre
possède une étiquette qui désigne une opération à exécuter. Il
s'obtient par des transformations simples à partir de l'arbre de
dérivation. On donne en exemple figure 6.3 l'arbre de
syntaxe abstraite correspondant à l'arbre de dérivation de la figure
6.2.
Figure 6.3 : Arbre de syntaxe abstraite de l'expression
6.4 Analyse descendante récursive
Deux principales techniques sont utilisées pour effectuer l'analyse
syntaxique. Il faut en effet, étant donnés une grammaire G et un mot f, de construire la suite des dérivations de G
ayant conduit de l'axiome au mot f,
S 0 ® u1 ® u2 ... un-1 ® un = f
La première technique consiste à démarrer de l'axiome et
à tenter de retrouver u1, puis u2 jusqu'à obtenir un = f,
c'est l'analyse descendante. La seconde, l'analyse
ascendante procède en sens inverse, il s'agit de commencer par
deviner un-1 à partir de f puis de remonter à un-2 et
successivement jusqu'à l'axiome S 0. Nous décrivons ici sur des
exemples les techniques d'analyse descendante, l'analyse ascendante
sera traitée dans un paragraphe suivant.
La première méthode que nous considérons s'applique à des cas très
particuliers. Dans ces cas, l'algorithme d'analyse syntaxique devient une
traduction fidèle de l'écriture de la grammaire. On utilise pour cela
autant de procédures qu'il y a d'éléments dans X chacune
d'entre elles étant destinée à reconnaître un mot dérivant de
l'élément correspondant de X. Examinons comment cela se passe
sur l'exemple de la grammaire des expressions infixes, nous
choisissons ici la deuxième forme de cette grammaire:
| E ® T | | T ® F | | F ® a |
| E ® T + E | | T ® F * T | | F ® (E)
| |
|
Que l'on traduit par les trois procédures récursives
croisées suivantes en Java. Celles ci construisent l'arbre de
syntaxe abstraite comme dans le chapitre 4.
class ASA {
char op;
ASA filsG, filsD;
ASA (char x, ASA a, ASA b) {
op = x;
filsG = a;
filsD = b;
}
static String f;
static int i = 0;
static ASA expression() throws ErreurDeSyntaxe {
ASA a = terme();
if (f.charAt(i) == '+') {
++i;
return new ASA('+', a, expression());
}
else return a;
}
static ASA terme() throws ErreurDeSyntaxe {
ASA a = facteur();
if (f.charAt(i) == '*') {
++i;
return new ASA ('*', a, terme());
}
else return a;
}
static ASA facteur() throws ErreurDeSyntaxe {
if (f.charAt(i) == '(') {
++i;
ASA a = expression();
if (f.charAt(i) == ')') {
++i;
return a;
}
else throw new ErreurDeSyntaxe(i);
}
else if (f.charAt(i) == 'a') {
++i;
return new ASA ('a', null, null);
}
else throw new ErreurDeSyntaxe(i);
}
}
Dans ce programme, le mot f à analyser est une variable
globale. Il en est de même pour la variable entière i qui
désigne la position à partir de laquelle on effectue l'analyse
courante. Lorsqu'on active la procédure expression, on
recherche une expression commençant en f[i]. A la fin de
l'exécution de cette procédure, si aucune erreur n'est détectée, la
nouvelle valeur (appelons la i1) de i est telle que
f[i]f[i+1] ... f[i1-1] est une expression. Il en est de même pour
les procédures terme et facteur. Chacune de ces
procédures tente de retrouver à l'intérieur du mot à analyser une
partie engendrée par E, T ou F. Ainsi, la procédure
expression commence par rechercher un terme. Un nouvel
appel à expression est effectué si ce terme est suivi par le
symbole +. Son action se termine sinon. La procédure
terme est construite sur le même modèle et la procédure
facteur recherche un symbole a ou une expression
entourée de parenthèses. Si une erreur de syntaxe est détectée, on
envoit une exception avec la position courante dans le mot à
reconnaitre, ce qui permettra de préciser l'endroit où l'erreur a été
rencontrée. La classe de l'exception est definie par:
class ErreurDeSyntaxe extends Exception {
int position;
public ErreurDeSyntaxe (int i) {
position = i;
}
}
Cette technique fonctionne bien ici car les membres droits des règles
de grammaire ont une forme particulière. Pour chaque élément S de
X, l'ensemble des membres droits {u1, u2... up} de règles,
dont le membre gauche est S, satisfait les conditions suivantes: les
premières lettres des ui qui sont dans A, sont toutes distinctes
et les ui qui commencent par une lettre de X sont tous facteurs
gauches les uns des autres. Beaucoup de grammaires de langages de
programmation satisfont ces conditions: Pascal, Java.
Une technique plus générale d'analyse consiste à
procéder comme suit. On construit itérativement des mots u dont on
espère qu'ils vont se dériver en f. Au départ on a u =
S0. A chaque étape de l'itération, on cherche la première lettre
de u qui n'est pas égale à son homologue dans f. On a ainsi
u = gyv f = gxh x¹ y
Si y Î A, alors f ne peut dériver de u, et il faut
faire repartir l'analyse du mot qui a donné u. Sinon y Î X et
on recherche toutes les règles dont y est le membre gauche.
y ® u1, y ® u2, ... y ® uk
On applique à u successivement chacune de ces règles, on obtient
ainsi des mots v1, v2, ... vk. On poursuit l'analyse, chacun
des mots v1, v2, ... vk jouant le rôle de u. L'analyse est
terminée lorsque u = f. La technique est celle de l'exploration
arborescente qui sera développée au Chapitre 8. On peut la
représenter par la procédure suivante donnée sous forme informelle.
static boolean Analyse (String u, f) {
if (f.equals(u))
return true;
else {
Mettre f et u sous la forme f= gxh, u=gyv où x ¹ y
if (y Ï A)
Pour toute règle y ® w faire
if (Analyse(g + w + v, f))
return true;
return false;
}
}
On écrit donc un programme comme suit en utilisant
la fonction estAuxiliaire(y) qui vaut vrai ssi y Î X. On
suppose que les mots f et u se terminent respectivement par
$ et #, il s'agit là de sentinelles permettant de
détecter la fin de ces mots. On suppose aussi que l'ensemble des
règles est contenu dans un tableau regle[S][i] qui donne la
i+1-ème règle dont le membre gauche est S. Le nombre de règles
dont le membre gauche est S est fourni par nbRegles[S].
static int pos = 1;
static boolean analyseDescendante (String u, String f) {
while (f.charAt(pos) == u.charAt(pos))
++pos;
if (f.charAt(pos) == '$' && u.charAt(pos) == '#')
return true;
else {
char y = u[pos];
if (estAuxiliaire(y))
for (int i = 0; i < nbRegles[y]; ++i) {
String v = u.substring(0, pos) + regle[y][i]
+ u.substring(pos+1);
if (Analyse (v, f))
return true;
}
return false;
}
}
Remarques
- Cette procédure ne donne pas de résultat lorsque la grammaire
est ce qu'on appelle récursive à gauche (le mot récursif n'a pas
ici tout à fait le même sens que dans les procédures récursives),
c'est à dire lorsqu'il existe une suite de dérivations partant d'un
S de X et conduisant à un mot u qui commence par S. Tel
est le cas pour la première forme de la grammaire des expressions
arithmétiques infixes qui ne peut donc être analysée par
l'algorithme ci dessus.
- Les transformations que l'on applique au mot u s'expriment
bien à l'aide d'une pile dans laquelle on place le mot à analyser,
sa première lettre en sommet de pile.
- Cette procédure est très coûteuse en temps lors de l'analyse
d'un mot assez long car on effectue tous les essais successifs des
règles et on peut parfois se rendre compte, après avoir pratiquement
terminé l'analyse, que la première règle appliquée n'est
pas la bonne. Il faut alors tout recommencer avec une autre règle et
éventuellement répéter plusieurs fois. La complexité de
l'algorithme est ainsi une fonction exponentielle de la longueur du
mot à analyser.
- Si on suppose qu'aucune règle ne contient un membre droit égal
au mot vide, on peut diminuer la quantité de calculs effectués en
débutant la procédure d'analyse par un test vérifiant si la
longueur de u est supérieure à celle de f. Dans ce cas, la
procédure d'analyse doit avoir pour résultat
false. Noter que
dans ces conditions la procédure d'analyse donne un résultat même
dans le cas de grammaires récursives à gauche.
6.5 Analyse LL
Une technique pour éviter les calculs longs de l'analyse descendante
récursive consiste à tenter de deviner la première règle qui a
été appliquée en examinant les premières lettres du mot f à
analyser. Plus généralement, lorsque l'analyse a déjà donné le
mot u et que l'on cherche à obtenir f, on écrit comme ci-dessus
f = gh, u = gSv
et les premières lettres de h doivent permettre de
retrouver la règle qu'il faut appliquer à S. Cette technique n'est
pas systématiquement possible pour toutes les grammaires, mais c'est
le cas sur certaines comme par exemple celle des expressions
préfixées ou une grammaire modifiée des expressions infixes. On dit
alors que la grammaire satisfait la condition LL.
Expressions préfixées
Nous considérons la grammaire de
ces expressions:
A = {+, *, (, ), a }, X = {S }, l'axiome est S, les
règles sont données par:
S ® (+ S S )
S ® (* S S)
S ® a
Pour un mot f de A*, il est immédiat de déterminer u1 tel que
En effet, si f est de longueur 1, ou bien f= a et le
résultat de l'analyse syntaxique se limite à S ® a, ou bien
f n'appartient pas au langage engendré par la grammaire.
Si f est de longueur supérieure à 1, il suffit de connaître les
deux premières lettres de f pour pouvoir retrouver u1. Si ces
deux premières lettres sont (+, c'est la règle S ® (+ S S
) qui a été appliquée, si ces deux lettres sont (* alors c'est
la règle S ® (* S S ). Tout autre début de règle conduit à un
message d'erreur.
Ce qui vient d'être dit pour retrouver u1 en utilisant les deux
premières lettres de f se généralise sans difficulté à la
détermination du (i+1)ème mot ui+1 de
la dérivation à partir de ui. On décompose d'abord ui et f
en:
ui = gi S vi f = gi fi
et on procède en fonction des deux premières lettres de fi.
- Si fi commence par a, alors ui+1 = giavi
- Si fi commence par (+, alors ui+1 = gi(+SS)vi
- Si fi commence par (*, alors ui+1 = gi(*SS)vi
- Un autre début pour fi signifie que f n'est pas une expression
préfixée correcte, il y a une erreur de syntaxe.
Cet algorithme reprend les grandes lignes de la descente récursive
avec une différence importante: la boucle while qui consistait
à appliquer chacune des règles de la grammaire est remplacée par un
examen de certaines lettres du mot à analyser, examen qui permet de
conclure sans retour arrière. On passe ainsi d'une complexité
exponentielle à un algorithme en O(n). En effet, une manière
efficace de procéder consiste à utiliser une pile pour gérer le mot
vi qui vient de la décomposition ui = gi S vi. La
consultation de la valeur en tête de la pile et sa comparaison avec
la lettre courante de f permet de décider de la règle à
appliquer. L'application d'une règle consiste alors à supprimer la
tête de la pile (membre gauche de la règle) et à y ajouter le mot
formant le membre droit en commençant par la dernière lettre.
Nous avons appliqué cette technique pour construire l'arbre de
syntaxe abstraite associé à une expression préfixée. Dans ce qui
suit, le mot à analyser f est une variable globale de même que la
variable entière pos qui indique la position à laquelle on se
trouve dans ce mot.
static Arbre ArbSyntPref() {
Arbre a;
char x;
if (f.charAt(pos) == 'a') {
a = NouvelArbre('a', null, null);
++pos;
} else if (f.charAt(pos) == '(' &&
(f.charAt(pos+1) == '+' || f.charAt(pos+1) == '*')) {
x = f.charAt(pos + 1);
pos = pos + 2;
a = NouvelArbre(x, ArbSyntPref(), ArbSyntPref());
if (f.charAt(pos) == ')')
++pos;
else
erreur(pos);
} else
erreur(pos);
return a;
}
L'algorithme d'analyse syntaxique donné ici peut s'étendre
à toute grammaire dans laquelle pour chaque couple de règles S ®
u et S ® v, les mots qui dérivent de u et v n'ont pas des
facteurs gauches égaux de longueur arbitraire. Ou de manière plus
précise, il existe un entier k tel que tout facteur gauche de
longueur k appartenant à A* d'un mot qui dérive de u est
différent de celui de tout mot qui dérive de v. On dit alors que
la grammaire est LL(k) et on peut alors démontrer:
Théorème 5 Si G est une grammaire LL(k), il existe un
algorithme en O(n) qui effectue l'analyse syntaxique descendante d'un
mot f de longueur n.
En fait, cet algorithme est surtout utile pour k =1. Nous donnons ici
ses grandes lignes sous forme d'un programme Pascal qui utilise une
fonction Predicteur(S, g) calculée au préalable. Pour un
élément S de X et un mot g de longueur k, cette fonction
indique le numéro de l'unique règle S ® u telle que u se
dérive en un mot commençant par g ou qui indique Omega si
aucune telle règle n'existe. Dans l'algorithme qui suit, on utilise
une pile comme variable globale. Elle contient la partie du mot u
qui doit engendrer ce qui reste à lire dans f. Nous en donnons ici
une forme abrégée.
static boolean Analyse(String f, int pos) {
int i;
pos = 1;
while (Pile.valeur(p) == f.charAt(pos)) {
Pile.supprimer(p);
++pos;
}
if (Pile.vide(p) && f.charAt(pos) == '$')
return true;
else {
y = Pile.valeur(p);
if (! estAuxiliaire(y))
return false;
else {
i = Predicteur (y, pos, pos+k-1);
if (i != Omega) {
System.out.println (y, '->', regle[y][i]);
Pile.inserer(regle[y,i], p);
return Analyse (f, pos);
} else
return false;
}
}
}
6.6 Analyse ascendante
Les algorithmes d'analyse ascendante sont souvent plus compliqués que
ceux de l'analyse descendante. Ils s'appliquent toutefois à un beaucoup
plus grand nombre de grammaires. C'est pour cette raison qu'ils sont très
souvent utilisés. Ils sont ainsi à la base du système yacc qui
sert à écrire des compilateurs sous le système Unix.
Rappelons que l'analyse ascendante consiste à retrouver la dérivation
S 0 ® u1 ® u2 ... un-1 ® un = f
en commençant par un-1 puis un - 2 et ainsi de
suite jusqu'à remonter à l'axiome S0. On effectue ainsi ce que
l'on appelle des réductions car il s'agit de remplacer un
membre droit d'une règle par le membre gauche correspondant, celui-ci
est en général plus court.
Un exemple de langage qui n'admet pas d'analyse syntaxique
descendante simple, mais sur lequel on peut effectuer une analyse
ascendante est le langage des systèmes de parenthèses. Rappelons sa
grammaire:
| S ® aS bS | | S ® aS b | | S ® abS | | S ® ab
| |
|
On voit bien que les règles S ® aSbS et S ® aSb
peuvent engendrer des mots ayant un facteur gauche commun
arbitrairement long, ce qui interdit tout algorithme de type LL(k).
Cependant, nous allons donner un algorithme simple d'analyse
ascendante d'un mot f.
Partons de f et commençons par tenter de retrouver la
dernière dérivation, celle qui a donné f = un à partir d'un mot
un-1. Nécessairement un-1 contenait un S qui a été
remplacé par ab pour donner f. L'opération inverse consiste donc
à remplacer un ab par S, mais ceci ne peut pas être effectué
n'importe où dans le mot, ainsi si on a
f= ababab
il y a trois remplacements possibles donnant
Les deux premiers ne permettent pas de poursuivre l'analyse. En
revanche, à partir du troisième, on retrouve abS et
finalement S. D'une manière générale on remplace ab par S
chaque fois qu'il est suivi de b ou qu'il est situé en fin de mot.
Les autres règles de grammaires s'inversent aussi pour donner des
règles d'analyse syntaxique. Ainsi:
- Réduire aSb en S s'il est suivi de b ou s'il est situé
en fin de mot.
- Réduire ab en S s'il est suivi de b ou s'il est situé en
fin de mot.
- Réduire abS en S quelle que soit sa position.
- Réduire aSbS en S quelle que soit sa position.
On a un algorithme du même type pour l'analyse des expressions
arithmétiques infixes engendrées par la grammaire:
| E ® T | | T ® F | | F ® a |
| E ® E + T | | T ® T * F | | F ® (E) |
| E ® E - T
| | |
|
Cet algorithme tient compte pour effectuer une réduction de
la première lettre qui suit le facteur que l'on envisage de réduire
(et de ce qui se trouve à gauche de ce facteur). On dit que la
grammaire est LR(1). La théorie complète de ces grammaires
mériterait un plus long développement. Nous nous contentons de
donner ici ce qu'on appelle l'automate LR(1) qui effectue
l'analyse syntaxique de la grammaire, récursive à gauche, des
expressions infixes. Noter que l'on a introduit l'opérateur de
soustraction qui n'est pas associatif. Ainsi la technique d'analyse
décrite au début du paragraphe
6.4 ne peut être appliquée ici.
On lit le mot à analyser de gauche à droite et on effectue les
réductions suivantes dès qu'elles sont possibles:
- Réduire a en F quelle que soit sa position.
- Réduire (E) en F quelle que soit sa position.
- Réduire F en T s'il n'est pas précédé de *.
- Réduire T*F en T quelle que soit sa position.
- Réduire T en E s'il n'est pas précédé de + et
s'il n'est pas suivi de *.
- Réduire E + T en E s'il n'est pas suivi de *.
- Réduire E - T en E s'il n'est pas suivi de *.
On peut gérer le mot réduit à l'aide d'une pile. Les
opérations de réduction consistent à supprimer des éléments dans
celle-ci, les tests sur ce qui précède ou ce qui suit se font très
simplement en consultant les premiers symboles de la pile. On peut
construire aussi un arbre de syntaxe abstraite en utilisant une autre
pile qui contient cette fois des arbres (c'est à dire des pointeurs
sur des noeuds). Les deux piles sont traitées en parallèle, la
réduction par une règle a pour effet sur la deuxième pile de
construire un nouvel arbre dont les fils se trouvent en tête de la
pile, puis à remettre le résultat dans celle-ci.
6.7 Evaluation
Dans la plupart des algorithmes que nous avons donnés, il a été
question d'arbre de syntaxe abstraite d'une expression arithmétique.
Afin d'illustrer l'intérêt de cet arbre, on peut examiner la
simplicité de la fonction d'évaluation qui permet de calculer la
valeur de l'expression analysée à partir de l'arbre de syntaxe
abstraite.
static int evaluer(Arbre x) {
if (x.valeur == 'a')
return x.valeur;
else if (x.valeur == '+')
return evaluer(x.filsG) + evaluer(x.filsD);
else if (x.valeur == '-')
return evaluer(x.filsG) - evaluer(x.filsD);
else if (x.valeur == '*')
return evaluer(x.filsG) * evaluer (x.filsD);
}
Une fonction similaire, qui ne demanderait pas beaucoup de mal à
écrire, permet de créer une suite d'instructions en langage machine
traduisant le calcul de l'expression. Il faudrait remplacer les
opérations +, *, -, effectuées lors de la
visite d'un noeud de l'arbre, par la concaténation des listes d'instructions qui calculent le sous-arbre droit et le sous
arbre gauche de ce noeud et de faire suivre cette liste par une
instruction qui opère sur les deux résultats partiels. Le programme
complet qui en résulte dépasse toutefois le but que nous nous fixons
dans ce chapitre.
6.8 Programmes en C
type asa =
Feuille of char
| Noeud of char * asa * asa;;
exception erreur_de_syntaxe of int;;
let f = " (a + a * a ) ";;
let i = ref 0;;
let rec expression () =
let a = terme () in
if f.[!i] = `+` then begin
incr i;
Noeud (`+`, a, expression ()) end
else a
and terme () =
let a = facteur () in
if f.[!i] = `*` then begin
incr i;
Noeud (`*`, a, terme ()) end
else a
and facteur () =
if f.[!i] = `(` then begin
incr i;
let a = expression () in
if f.[!i] = `)` then begin
incr i;
a end
else raise (erreur_de_syntaxe !i) end
else
if f.[!i] = `a`
then begin
incr i;
Feuille `a` end
else raise (erreur_de_syntaxe !i);;
(* Prédicat définissant les non-terminaux *)
let est_auxiliaire y = ... ;;
(* règle.(s).(i) est la ième règle
dont le membre gauche est s *)
let règle =
[| [| s00; s01; ... |];
[| s10; s11; ... |];
[| si0; si1; ... |];
... |];;
(* nbrègle.(s) est le nombre de règles
dont le membre gauche est s *)
let nbrègle = [| s0; ...; sn |];;
(* Fonction auxiliaire sur les chaînes
de caractères: remplacer s pos char
renvoit une copie de la chaîne s
avec char en position pos *)
let remplacer s pos char =
let s1 = make_string (string_length s) ` ` in
blit_string s 0 s1 0 (string_length s);
s1.[pos] <- char;
s1;;
let analyse_descendante f u =
let b = ref false in
let pos = ref 0 in
while f.[!pos] = u.[!pos] do incr pos done;
if f[!pos] = `$` && u.[!pos] = `#`
then
true
else
let y = u.[!pos] in
if est_auxiliaire y
then begin
let i = ref 0 in
let ynum = int_of_char y - int_of_char `A` in
while not !b && !i <= nbrègle.(ynum) do
b := analyse_récursive
(remplacer (u, !pos, règle.(ynum).(!i)), f);
else incr i
done;
!b end
else false;;
(* Analyse LL(1), voir page X *)
let rec arbre_synt_pref () =
if f.[!pos] = `a`
then begin
incr pos;
Feuille `a` end
else
if f.[!pos] = `(`
&& f.[!pos + 1] = `+`
|| f.[!pos + 1] = `*`
then begin
let x = f.[!pos + 1] in
pos := !pos + 2;
let a = arbre_synt_pref () in
let b = arbre_synt_pref () in
if f.[!pos] = `)`
then Noeud (x, a, b)
else erreur (!pos) end
else erreur(!pos);;
(* Évaluation, voir page X *)
type expression =
| Constante of int
| Opération of char * expression * expression;;
let rec évaluer = function
| Constante i -> i
| Opération ('+', e1, e2) -> évaluer e1 + évaluer e2
| Opération ('*', e1, e2) -> évaluer e1 * évaluer e2;;