


Next: Publications
Up: ENS
Previous: ENS
At ENS, work has progressed in game semantics and in the investigation
of Boudol's calculus of resources.
Game semantics. A key interest of game
semantics is that it provides a framework within which one may conciliate
dynamic and static aspects of meaning. It is expected that such
semantics can help in complexity theory on the one hand and in
extending denotational semantics to model concurrent and distributed
languages (so-called process-calculi).
- 1.
- In [DHR96], V. Danos, H. Herbelin and L. Regnier
explain the operational side of the two
game models of Hyland-Ong (HO) and Abramsky-Jagadeesan-Malacaria
(AJM) in terms of abstract machines. Building on this explanation,
an
embedding of the AJM model in the HO model is given that leads to
aneasy proof of completeness for the former.
- 2.
- In [BDER97], P. Baillot, V. Danos, T. Ehrhard and L.
Regnier adapt the AJM
construction to give the first known games model which
encompasses all of classical linear logic. Composition of
strategies is recast as a communication process. The exponential part
of the
model is based on the idea of sticking to strategies which contain
all possible encodings of copy-tags. This works is pursued in
[BDER97b], which gives an explicit
transformation that goes from that linear logic games model to the
traditional relational model. This concrete extensional collapse
helps in understanding what games semantics is good to.
- 3.
- In [CuBoeh]
P.-L. Curien presents a formalism of trees with pointers, called
abstract Böhm trees, that provide a suitable abstract framework in
which various cut-free proofs or normal terms of several
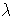 -calculus
based languages (including
-calculus
based languages (including 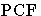 and Parigot's
and Parigot's 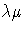 -calculus)
can be faithfully encoded. A simple abstract machine allows us to
compute over abstract Böhm trees. This machine
is closely related to Coquand's interaction sequences and
debates. The execution over finite abstract Böhm trees always
terminates. We introduce an abstract notion of type that
fits the purpose of guaranteeing that the execution cannot go into
deadlock, i.e., that it always reaches a satisfactory final state.
The operational aspects of (untyped) Böhm trees are investigated
in more depth in [CuHer96], a joint paper by P.-L. Curien and
H. Herbelin,
-calculus)
can be faithfully encoded. A simple abstract machine allows us to
compute over abstract Böhm trees. This machine
is closely related to Coquand's interaction sequences and
debates. The execution over finite abstract Böhm trees always
terminates. We introduce an abstract notion of type that
fits the purpose of guaranteeing that the execution cannot go into
deadlock, i.e., that it always reaches a satisfactory final state.
The operational aspects of (untyped) Böhm trees are investigated
in more depth in [CuHer96], a joint paper by P.-L. Curien and
H. Herbelin,
Calculus with resources (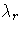 ).
C. Lavatelli has been working on the definition of an
algebraic semantics of
).
C. Lavatelli has been working on the definition of an
algebraic semantics of 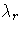 based on approximants,
in the flat scenario (where both abstractions and deadlock are
observable),
which turns out to be sound. Work in progress concerns completeness.
The aim is to use these results as intermediate steps in the
characterization of the flat semantics through an intersection
type system. Another work in progress, by C. Lavatelli and P.-L.
Curien, concerns the use of techniques of logical relations to
compare the inequational theories of two models of
based on approximants,
in the flat scenario (where both abstractions and deadlock are
observable),
which turns out to be sound. Work in progress concerns completeness.
The aim is to use these results as intermediate steps in the
characterization of the flat semantics through an intersection
type system. Another work in progress, by C. Lavatelli and P.-L.
Curien, concerns the use of techniques of logical relations to
compare the inequational theories of two models of 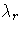 that
have arisen naturally when trying to give a semantics to
that
have arisen naturally when trying to give a semantics to
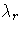 .
.



Next: Publications
Up: ENS
Previous: ENS
1/10/1998
![]()
![]()
![]()
![]()
![]() ).
C. Lavatelli has been working on the definition of an
algebraic semantics of
).
C. Lavatelli has been working on the definition of an
algebraic semantics of ![]() based on approximants,
in the flat scenario (where both abstractions and deadlock are
observable),
which turns out to be sound. Work in progress concerns completeness.
The aim is to use these results as intermediate steps in the
characterization of the flat semantics through an intersection
type system. Another work in progress, by C. Lavatelli and P.-L.
Curien, concerns the use of techniques of logical relations to
compare the inequational theories of two models of
based on approximants,
in the flat scenario (where both abstractions and deadlock are
observable),
which turns out to be sound. Work in progress concerns completeness.
The aim is to use these results as intermediate steps in the
characterization of the flat semantics through an intersection
type system. Another work in progress, by C. Lavatelli and P.-L.
Curien, concerns the use of techniques of logical relations to
compare the inequational theories of two models of ![]() that
have arisen naturally when trying to give a semantics to
that
have arisen naturally when trying to give a semantics to
![]() .
.