Grammaires
Analyse grammaticale.
Postscript, PDF Didier Rémy Polytechnique, INRIA
Cours (super, self) Exercises
  1. Grammaires, dérivations, ambiguités
  2. Élimination des ambiguités
  3. Grammaires LL
  4. Grammaires LR
  5. Élimination des conflits
  6. Ocamlyacc
  1. Langage de parenthèses (*)
  2. Expressions arithmétiques (*)
  3. Travaux dirigés (**)
Cours (super, self) Exercises
  1. Grammaires, dérivations, ambiguités
  2. Élimination des ambiguités
  3. Grammaires LL
  4. Grammaires LR
  5. Élimination des conflits
  6. Ocamlyacc
  1. Langage de parenthèses (*)
  2. Expressions arithmétiques (*)
  3. Travaux dirigés (**)


Grammaires algébriques (context-free)


Une grammaire permet une représentation finie d'un langage (éventuellement infini). Noam Chomsky (c.f. author of Manufacturing Conscent) a inventé la notion de grammaire formelle.

Une grammaire algébrique (ou context free) G est un quadruplet (S, V, S, P) où:
    ·S est l'alphabet des terminaux (lexèmes ou tokens),
    ·V est l'alphabet des non-terminaux (disjoint de S),
    ·S Î V est l'unique axiome.
    ·P est un ensemble fini de règles de production,

de la forme a ® b avec a Î V, et b Î (S È V)*


Le langage L(G) associé à la grammaire G est la fermeture transitive du singleton { S } par la règle d'induction:
u a v Î L Ù a ® b Î P Þ u b v Î L


Dérivations


Pour montrer qu'un mot w est dans le langage L il faut donc exhiber une suite finie d'applications de règles de production partant de S et aboutissant à w, appelée une dérivation.

On peut représenter une dérivation par
S = w0 ®P1 w1 ®P2 ... ®Pn wn = w
où wk = uk bk vk = uk+1 ak+1 vk+1 et Pk = ak ® bk.

On laisse Pi implicite lorsqu'il n'y a pas d'ambiguité, ou on écrit:
S =
u1 a1 v1 ® u1
b1
v1 = u2 a2 v2 ® u2
b2
v2 =...
 
un an vn ® un
bn
vn


Exemples: expressions arithmétiques


Les terminaux (lexèmes) sont NUM, ID,  PLUS  et  MINUS .
S ® E    E ® NUM    E ® ID      E ® E  PLUS  E      E ® E  MINUS  E
Pour reconnaître l'expression 1 - 1 + x, ie. après analyse lexicale, NUM  MINUS  NUM  PLUS  ID, il existe de nombreuses dérivations possibles. L'ensemble de ces dérivations peut être représenté par un ensemble d'arbres syntaxiques (ici deux):
S ® E ®
ì
ï
ï
í
ï
ï
î
E ® ì
í
î
E ® NUM
 MINUS 
E ® NUM
 PLUS 
E ® ID
  
S ® E ®
ì
ï
ï
í
ï
ï
î
E ® NUM
 MINUS 
E ® ì
í
î
E ® NUM
 PLUS 
E ® ID
Chaque arbre syntaxique représente lui même un ensemble de dérivations obtenues en fixant un ordre d'application des règles.

Dérivations


Par exemple, la dérivation la plus à gauche (resp. à droite) de l'arbre syntaxique de gauche est obtenue en réduisant toujours le non-terminal le plus à gauche (resp. à droite). Le bleue indique la partie réduite dans la ligne suivante. Le rouge indique la partie qui vient d'être réduite, donc correspondant à la partie bleue de la ligne précédente.
S
E
E  PLUS  E
E  MINUS  E  PLUS  E
NUM MINUS  E  PLUS  E
NUM  MINUS  NUM  PLUS  E
NUM  MINUS  NUM  PLUS  ID
   resp.  
S
E
E  PLUS  E
E  PLUS  ID
E  MINUS  E  PLUS  ID
E  MINUS  NUM  PLUS  ID
NUM MINUS  NUM  PLUS  ID
Parmi l'ensemble des dérivations d'un arbre syntaxique, il en existe toujours une la plus à gauche (resp. la plus à droite).

Grammaires régulières


Les règles de production sont de la forme a ® b où b Î {e} È S V.

Langage régulier Le langage décrit par une grammaire régulière peut être reconnu par un automate fini, et réciproquement.
    ·À (S, V, S, P), on associe (V È {F}, S, d, S, {F}) où q' Î d (q, a) si q ® a q' et q Î F si q ® e.
    ·À un automate fini déterministe (Q, S, d, q0, F) on associe la grammaire (S, Q, q0, P) où P contient q ® a q' si q' Î d (q, a) et q ® e si q' Î F.


Exemple à l'expression régulière (ab)* correspond la grammaire composée des lexèmes a et b et des règles:
S ®            S ® a I            I ® b S           
Un exemple de dérivation:
S ®
a I
® a
b S
® a b
a I
® a b a
b S
® abab

Grammaires ambigües


Dérivations et arbres de dérivations
    ·En général, il existe de nombreuses dérivations d'un même arbre syntaxique, mais ce n'est pas gênant.
    ·Lorsqu'il existe plusieurs arbres syntaxiques dérivables pour une même expression, la grammaire est dite ambigüe.


Élimination des ambiguités

L'existence de plusieurs arbres syntaxiques pose un problème, car il faudra faire un choix dans la construction de l'arbre de syntaxe abstraite qui va en général influer sur la sémantique (par exemple, la soustraction des expressions arithmétiques n'est pas associative).

Heureusement, il est souvent possible d'éliminer les ambiguités, ce qui consiste à ré-écrire certaines règle de façon à obtenir une grammaire non-ambigüe reconnaissant le même langage.

Élimination des ambiguïtés


Typiquement, on peut séparer un terminal E en deux terminaux E et T.
S ® E
E ® E  PLUS  T
E ® E  MINUS  T
      
E ® T
T ® NUM
T ® ID


Fin de fichier/phrase on ajoute un lexème  EOF  et
    ·on change les règles S ® a en S ® a  EOF , ou bien
    ·on introduit un symbole S' et on prend S' ® S  EOF  pour axiome (S devient un non-terminal).


Grammaires prédictives LL(1)


Simples, elles permettent l'écriture manuelle d'analyseurs.

Pour b Î (S È V)*, on définit l'ensemble first(b) des lexèmes qui peuvent commencer une dérivation de b. Formellement,
first (b) = { a Î S | $ g Î (S È V)*, b ® *a g}
Une grammaire est prédictive (i.e. LL(1)), si pour tout non terminal a Î V, pour toutes productions distinctes a ® b et a ® b' alors first (b) Ç first (b') = Ø.

Généralisation possible à LL(k) mais peu utilisée (inefficacité)

Exemple: la grammaire des expressions arithmétiques donnée ci-dessus n'est pas prédictive, car:
first (E  PLUS  T) = {NUM, ID}= first (E  MINUS  T) = {NUM, ID}


Élimination de la récursion gauche


La récursion gauche est une source de d'ambiguité (conflit). On peut l'éliminer en par tansformation (réécriture) en des règles équivalentes, sans récursion gauche.
Exemple    æ
ç
ç
è
E ® E  PLUS  T
E ® E  MINUS  T
E ® T
ö
÷
÷
ø		   Þ     æ
ç
ç
ç
è
E ® T   E '
E ' ®  PLUS  T   E '
E ' ®  MINUS  T   E '
E ' ® e
ö
÷
÷
÷
ø
Cas général   æ
ç
ç
ç
è
X ® X   b1
X ® X   b2
X ® g1
X ® g2
ö
÷
÷
÷
ø		     Þ     æ
ç
ç
ç
ç
è
X ® g1   X '
X ® g2   X'
X' ® b1   X'
X' ® b2   X'
X' ® e
ö
÷
÷
÷
÷
ø		   


Factorisation gauche


Elle se traite de façon similaire.

Exemple du if-then-else
æ
è
E ®  IF  B  THEN  E  ELSE  E
E ®  IF  B  THEN  E
ö
ø		   Þ   æ
ç
ç
è
E ®  IF  B  THEN  E   X
X ®  ELSE  E
X ® e
ö
÷
÷
ø


Analyseur pour les grammaires prédictives


Pour chaque non-terminal a Î V, on peut décider de la production à appliquer en fonction du prochain lexème aÎ S: c'est l'unique règle a ® b avec a Î first (b) (puisque deux règles dérivant a ne peuvent pas commencer par le même lexème).

On peut alors construire une table à deux dimensions V × S à valeurs dans P.

Exemple pour les expressions arithmétiques (après élimination de la récursion gauche).
   PLUS   MINUS  ID NUM  EOF 
S     E  EOF  E  EOF   
E     T  E' T  E'  
E'  PLUS  T E'  MINUS  T  E'     e
T     ID NUM  


Programme d'analyse


La table ci-dessus peut être implémentée directement en interprétant le tableau ou bien par filtrage. (Il faudrait aussi ajouter un rattrapage d'erreur dans les cases vides du tableau):

Fichier expr.ml
type lexème = PLUS | MINUS | ID | NUM  | EOF;;
let buf = ref [];;
let lit_lexème() =
  match !buf with h::t -> buf:= t; h | [] -> EOF;;
let lexème =  ref (EOF : lexème);;
let avance() = lexème := lit_lexème();;
let accepte a =
  if !lexème = a then avance() else failwith "accepte"
let rec _S() =
  match !lexème with
  | ID | NUM -> _E(); accepte EOF
and _E() =
  match !lexème with
  | ID | NUM -> _T(); _E'() 
and _E'() =
  match !lexème with
  | PLUS -> accepte PLUS; _T(); _E'() 
  | MINUS -> accepte MINUS; _T(); _E'() 
  | EOF -> () 
and _T() =
  match !lexème with
  | ID -> accepte ID; 
  | NUM -> accepte NUM

let parse l = buf := l; avance(); _S();;


Langages LR(1)


Left-to-right parse, Right-most derivation (1-token lookahead)


Les grammaires LL(1) permettent l'écriture facile donc manuelle d'analyseurs, mais l'écriture d'une grammaire LL(1) pour un langage est contraignante et revient à une forme de ``compilation manuelle''. De plus, celle-ci n'est pas toujours possible.

Les grammaires LR sont plus générales: une grammaire LR(1) est aussi LL(1) donc la classe des langages reconnus par une grammaire LR(1) contient celle des langages LL(1).

Les grammaires LR(1) sont également plus souples (moins contraignantes) dans l'écriture des règles.

Principe


Leur moteur utilise une pile auxiliaire. Le flux de lexème est lu en consultant au plus 1 lexème non empilé. Il faut alors pouvoir décider d'une action à effectuer (en fonction de la pile et du prochain lexème):
    · shift, ie. consommer et empiler un lexème, ou

    ·reduce, ie. réduire une règle. Cela revient à appliquer une règle de production sur le sommet (partie droite) de la pile.
Si pour une même configuration de pile et du prochain lexème, plusieurs axiomes sont possibles, alors la grammaire n'est pas LR(1) et dite ambigüe.

Généralisation possible en regardant les k prochains lexèmes (grammaires LR(k)) mais peu utilisée (inefficacité).

Exemple de trace d'exécution
Pile          Flux de lexèmes Action
............................ NUM MINUS  NUM  PLUS  ID  EOF  shift
NUM ............................  MINUS NUM  PLUS  ID  EOF  reduce
T ............................  MINUS NUM  PLUS  ID  EOF  reduce
E ............................  MINUS NUM  PLUS  ID  EOF  shift
E  MINUS  ............................ NUM PLUS  ID  EOF  shift
E  MINUS  NUM ............................  PLUS ID  EOF  reduce
E  MINUS  T ............................  PLUS ID  EOF  reduce
E ............................  PLUS ID  EOF  shift
E  PLUS  ............................ ID EOF  shift
E  PLUS  ID ............................  EOF  reduce
E  PLUS  T ............................  EOF  reduce
E ............................  EOF  shift
E  EOF  ............................ reduce
S ............................  


Reconnaissance par un automate à pile


Une grammaire LR(1) est reconnaissable par un automate à pile qui mécanise le calcul précédent.

Description
    ·Les éléments sur la pile sont des paires (Xi, si) d'un état si et d'un lexème X Î S È V sauf le fond de pile qui est l'état initial s0.
    ·L'automate est déterminé par deux fonctions partiellement définies:
    ·goto (s, X) pour X Î S È V.
    ·action (s, a) qui peut prendre les valeurs shift ou reduce(P) où P est une règle de production


Transitions


Dans une configuration de pile s0 (X1, s1) ... (Xm, sm) (sommet à droite), l'automate consulte le lexème suivant a et par cas sur la valeur de action (sm, a) effectue l'une des deux actions:
    · shift: le prochain lexème est consommé et (a, goto (sm, a)) est empilée
    ·reduce(X ® a): k éléments où k est la longueur de a sont dépilés et (X, goto (sm-k, X)) est empilé.
Lorsque action (sm, ai) est indéfinie, l'automate s'arrête, avec succès si la pile est réduite à l'axiome, avec échec sinon.

Construction des états


Un état I est composé d'un ensemble de configurations C.

Une configuration C est une paire composée:
  1. d'une règle de production pointée a ® b . g. ie. a ® bg est une règle de production et b est le sommet de pile.

  2. du prochain lexème possible aÎ S.
La fermeture d'un ensemble de configurations I est le plus petit ensemble contenant I et satisfaisant
( (X ® a · Y b, a) Î I Ù Y ®g Î G Ù b Î first (b a) ) Þ (Y ®· g, b) Î I
La transition d'une configuration I par un lexème XÎ S È V est
goto (I,Y) = fermeture ( {(X ® a Y · b, a) | (X ® a · Y b, a) Î I} )


Construction des tables


L'état initial est la fermeture de l'axiome. Les états sont les ensembles de configurations fermées non vides atteignables par une suite de transitions arbitraires à partir de l'état initial.

Les actions sont de 4 types:
  1. Si (X ® a · a b, b) Î I et goto (I, a) = J, alors action (I,a) = shift

    (on peut représenter simultanément goto(I,a) en écrivant shift(J))

  2. Si (X ® a ·, a) Î I, alors action (I,a) = reduce(X ® a).

    Sauf, si X ® a est l'axiome, alors action (I,a) = accept.
(Il reste à représenter la table goto (I, Y) pour Y Î V.)

Enfin, la grammaire n'est pas LR(1) s'il y a des conflits, ie. plusieurs valeurs possibles pour action (I,a).

Pour les autres cases, action (I,a) = echec.
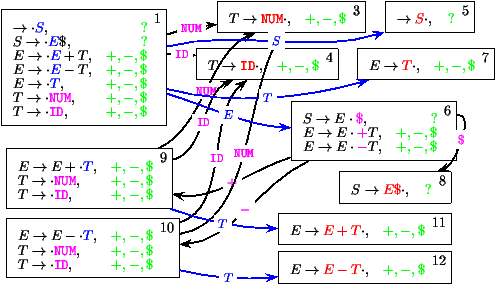
États (expressions arithmétiques)


Voir aussi la construction incrémentatle annimée en Postscript.



LR(0) v.s. LR(1)


Dans la construction précédente, l'ensemble des lexèmes prossibles après le déclanchement d'une règle est presque toujours  EOF ,  PLUS ,  MINUS , et ne sert jamais à déambigüer deux états.

En effet, l'exemple considérer est aussi LALR(0).

Exercice 1   On considère la grammaire suivante
S® E EOF 

E ® T  PLUS  E

E ® T

T ® ID
Vérifier que la grammaire n'est pas LR(0). (On construit les états comme pour une grammaire LR(1), mais dans lesquelles les configurations ne comporte que les premières composante (une règle pointée. Il suffit alors de vérifier qu'il existe deux transition possibles avec une même étiquette).

Vérifier que la grammaire est LR(1).


Construction de la table de l'automate


On construit un tableau de dimension 2 avec les états en ordonnées et les éléments de lettre de l'alphabet S È V en abscisse.

On remplit le tableau ligne par ligne. Pour chaque état I,
    ·Pour chaque flèche étiquettée par un terminal I ® a J, on associe une action shift(J) dans la colonne a.
    ·Pour chaque flèche étiquettée par un non-terminal I ® a J, on associe on mémorise la valeur J de goto(I,a) dans la case a. (pseudo-action shift(J)).
Enfin, pour chaque règle pointée à la fin (en rouge) on associe une action réduce dans la case associé à chacun des terminaux suivant possibles (en vert).

Tables
I + - NUM ID $ S E T
1     s 3 s 4   5 6 7
3 r 5 r 5     r 5      
4 r 6 r 6     r 6      
5                
6 s 9 s 10     s 8      
7 r 4 r 4     r 4      
8 r 1 r 1     r 1      
9     s 3 s 4       11
10     s 3 s 4       12
11 r 2 r 2     r 2      
12 r 3 r 3     r 3      
    
r règle
1 S ® E $
2 E ® E + T
3 E ® E - T
4 E ® T
5 T ® NUM
6 T ® ID
Exemple de trace d'exécution


Pile            Flux de lexèmes Action
1 ............................ NUM MINUS  NUM  PLUS  ID  EOF  shift
1 NUM3 ............................  MINUS NUM  PLUS  ID  EOF  reduce
1 T7 ............................  MINUS NUM  PLUS  ID  EOF  reduce
1 E6 ............................  MINUS NUM  PLUS  ID  EOF  shift
1 E6  MINUS  ............................ NUM PLUS  ID  EOF  shift
1 E6  MINUS 10 NUM3 ............................  PLUS ID  EOF  reduce
1 E6  MINUS 10 T12 ............................  PLUS ID  EOF  reduce
1 E6 ............................  PLUS ID  EOF  shift
1 E6  PLUS 9 ............................ ID EOF  shift
1 E6  PLUS 9 ID4 ............................  EOF  reduce
1 E6  PLUS 9 T11 ............................  EOF  reduce
1 E6 ............................  EOF  shift
1 E  EOF 8 ............................ reduce
1 S5 ............................  


Correction


Exercice 2  [Correction]   Vérifier que lorsque l'algorithme ci-dessus trouve une solution, alors il est possible de construire une dérivation.


Exercice 3  [Compléture]   Vérifier que lorsque l'algorithme ne trouve pas de solution, alors il n'existe pas de dérivation.


Conflits


Un conflit se produit lorsqu'il existe plusieurs une configuration (I,a) pour laquelle action(I,a) admet plusieurs valeurs possibles.

On parle de conflit:
    ·
reduce-reduce
lorsque (X ® a ·, a) Î I et (Y ® b ·, a) Î I.

Ces conflits sont graves et correspondent généralement à une forte ambiguïté dans la grammaire. Il faut réécrire la grammaire.
    ·
shift-reduce
lorsque (X ® a · a g, b) Î I et (Y ® b ·, a) Î I.

Ces conflits sont moins graves, et correspondent souvent à des priorités qu'il faut rendre explicites, soit par réécriture, soit par ajout de règles de priorité.
(Par construction, les conflits shift- shift ne sont pas possibles)

Règles d'associativité


La grammaire suivante contient un conflit shift/reduce
1 : E ® E + E          2: E ® NUM
En effet, la séquence NUM  PLUS  NUM  PLUS  NUM est reconnue par
shift, reduce2, shift, shift, reduce2, ì
í
î
reduce1, shift, reduce2, reduce1
shift, reduce2, reduce1, reduce1
La première solution reconnaît (E +E) + E, l'autre E + (E + E).

On peut réécrire la grammaire pour forcer l'une ou l'autre règle, mais il est aussi possible et préférable (bien que sortant du formalisme LR(1)) de choisir entre les deux actions possibles par des règles d'associativité et de priorité.

(Les règles de priorité s'appliquent localement pour ordonner les actions possibles à partir d'un état ambigü.)

Règles de priorité


Selon que + est déclaré associative à gauche ou à droite, l'action retenue sera reduce ou shift.

On peut également déclarer des lexèmes plus prioritaires que d'autres, ou des règles plus prioritaires que d'autres.

Grammaires LALR(1)


Look Ahead LR(1)

Les grammaires LALR(1) sont une restriction des grammaires LR(1) afin d'obtenir des tables plus petites. Le langage reconnu est un peu plus restrictif, mais ce n'est pas une gêne en pratique.

Dans une grammaire LALR(1) les états qui ne sont distingués que par le lexème suivant (mais qui ont exactement le même ensemble de règles de production) sont identifiés (avant construction des tables).

Yacc, Ocamlyacc, Bison, etc., sont des compilateurs de grammaires LALR(1).

Ocamlyacc


Fichier foo.mly
%{ 
  (* prelude : code Ocaml reproduit verbatim *)
%}
  /* declarations yacc */
%%
  /* règles yacc */
%%
  (* postlude : code Ocaml reproduit verbatim *)


Pour compiler la grammaire
ocamlyacc -v foo.mly         # produit foo.ml et foo.output
ocamlc foo.ml
L'option -v copie les tables dans un fichier foo.output (utile pour la mise au point)

Exemple


exp.mly
%token EOP PLUS MINUS 
%token <int> NUM
%token <string> ID
%start _S
%type <string> _S
%%
_S : _E EOP             { ($1 : string) } 
_E : _E PLUS _T         { "Plus ("^$1^", "^$3^")" } 
   | _E MINUS _T        { "Minus ("^$1^", "^$3^")" } 
   | _T                 { $1 } 
_T : NUM                { "Num "^(string_of_int $1) } 
   | ID                 { "Id "^$1 } 
%%


Indication des priorités


Dans la partie déclaration:
    %noassoc lower
    %left PLUS MINUS
    %left TIMES DIV
    %right FOO 
    %noassoc BAR
    %noassoc higher
Par défaut, la priorité d'une règle est celle de son dernier lexème.

La directive %prec peut être utilisée à la fin d'une règle pour indiquer la priorité à donner à cette règle.

Mise en oeuvre


Il faut combiner le parseur avec un lexeur. voir lexp.mll.

Le parseur doit être compilé en premier, car il produit simultanément la définition du type des token utilisé par le lexeur (le nom de l'identificateur token est fixé par convention).

Le programme principal appelle le parseur qui appelle le lexeur comme ci-dessus.

Report d'erreur

Il existe un mécanisme de report d'erreur dans yacc, mais qui n'est pas facile à mettre en oeuvre. En cas d'erreur, il est simple et souvent suffisant de signaler le dernier lexème lu et son emplacement (voir le compilateur Pseudo-Pascal main.ml)

Exercices


Exercice 4  [Langage de parenthèses]   Écrire un parseur (et un lexeur) pour le langage de parenthèses.

Comparer avec la reconnaissance des parenthèses directement dans le lexeur. Quelle approche est-elle préférable?
Réponse
Cela dépend du context: les commentaires parenthésés peuvent être reconnu directement par le lexeur, car la structure à l'intérieur du commentaire est ignoré (sauf le nombre de commentaires emboîtés). Pour les parenthèses autour des expressions, la structure à l'intérieur des parenthèses est important, et c'est plus naturelle/facile de les reconnaître directement dans le parseur.


Exercice 5  [Expressions arithmétiques]   Écrire un parseur (et un lexeur) pour reconnaître les expressions arithmétiques sans variables. Retourner l'arbre de syntaxe abstraite.

En déduire une calculette en remplaçant la génération de l'arbre par le calcul.

Pour obtenir une Super calculette, on pourra
    ·Ajouter des mémoires (set n et get n).
    ·Ajouter la comparaison et les expressions conditionnelles.


Travaux dirigés


Exercice 6  [Pseudo Pascal]   Écrire un lexeur pour le langage Pseudo Pascal. (On réutilisera le lexeur de cet exercice).

Un exemple de programme Pseudo Pascal est fact.p.

La syntaxe programmes est donnée dans une forme BNF (Backus Normal Form) que l'on peut lire comme des règles de production, une par ligne (le symbole | remplace un saut à la ligne).

La notation  u  s ... u  (resp.   u  s ... u  s ) représente une séquence possiblement vide de u séparés par des s (resp. et terminée par un s).

Programmes
p ::= program   v ; ... v ;    d ; ... d ;  i ;; Programme
Déclarations
v ::= var x : t Décl. de variable
d ::= function x (  var x : t , ... var x : t  ) : t;   v ; ... v ;  i Décl. de fonction
    procedure x (  var x : t , ... var x : t  );   v ; ... v ;  i Décl. de procédure
Instructions
i ::= x := e Affectation
    begin  i ; ... i   end Séquence
    if e  then  i  else  i Conditionnelle
    x ( e , ... e ) Appel de procédure
    read (x) Lecture
    write (e) Écriture
    writeln (e) Écriture avec newline
    e[e] := e Affectation de tableau
Expressions
e ::= (e) Expression parenthèsée
    x Variables
    n Entiers
    true | false Booléens
    x ( e , ... e ) Appel de fonction
    alloc ( e : t) Allocation
    e bin e Opération binaire
    e [ e] Accès dans un tableau
Opérations
bin ::= + | - | × | / Arithmétiques
    | | =| = | =| Comparaison
Types
t ::= integer
    boolean
    array of t
Dans un premier temps, on pourra laisser les actions vides (on retour unit). Ensuite, on produira un arbre de syntaxe abstraite défini par le type concret program du fichier d'interface pp.mli.
Réponse
parser.mly

Enfin, on pourra compléter le programme avec un imprimeur qui imprime le programme (arbre de syntaxe abstraire reconnu) dans la sortie standard. En particulier, cela permet de vérifier que le programme a été compris correctememt.
Réponse
print.ml


This document was translated from LATEX by HEVEA.