Le cube de Rubik, ou
Calculer dans un groupe de permutations

Le cube de Rubik est un jeu qui a passionné de nombreux adeptes il y a quelques années déjà. Le but de ce projet est de représenter ce cube sur ecran et de programmer certains algorithmes dans les groupes de permutations permettant de résoudre le problème combinatoire qui le concerne.

Ce projet comporte une partie graphique consistant à représenter le mieux possible le cube de Rubik et une partie de calcul algébrique dans le groupe des transformations engendré par les six transformations élémentaires du cube.

Ceux qui souhaitent approfondir leurs connaissances sur les calculs dans le groupe symetrique peuvent traiter rapidement la première partie et se consacrer plus longuement à la seconde. Au contraire ceux qui s'interessent à l'infomatique graphique pourront developper largement les procèdures de dessin et ne réaliser qu'un minimum de fonctions de calcul sur les permutations. Néanmoins il est quand même demandé pour chaque projet de traiter les deux parties.

1 Le cube Hongrois

Le cube Hongrois comporte six faces (comme tout cube qui se respecte !), chacune de ces six faces est divisée en 9 facettes. Il y a six mouvements possibles consistant à faire une rotation élémentaire d'un angle de p/2 de l'une des faces. La rotation autour d 'une face A affecte les 9 facettes de A et 12 facettes des faces adjacentes à A. Les facettes situées au centre de chacune des faces sont invariantes par toutes les rotations. On peut ainsi ne considérere que les 48 facettes qui sont déplacées par les rotations. Le cube et la numérotation des facettes est donné Figure 1.

Les faces sont appelées A,B,C,D,E,F et les rotations autour de chacune d'elles seront notées par les mêmes lettres. Celles ci sont des permutations sur {1,2 ..., 48}, on les donne ci dessous écrites comme un produit de cycles, les cycles de longueur un ne sont pas écrits.

A =	(1,3,8,6)	(2,5,7,4)	(9,48,15,12)	(10,47,16,13)	(11,46,17,14)
B =	(6,15,35,26)	(7,22,34,19)	(8,30,33,11)	(12,14,29,27)	(13,21,28,20)
C=	(1,12,33,41)	(4,20,36,44)	(6,27,38,46)	(9,11,26,24)	(10,19,25,18)
D=	(1,24,40,17)	(2,18,39,23)	(3,9,38,32)	(41,43,48,46)	(42,45,47,44)
E=	(3,43,35,14)	(5,45,37,21)	(8,48,40,29)	(15,17,32,30)	(16,23,31,22)
F=	(24,27,30,43)	(25,28,31,42)	(26,29,32,41)	(33,35,40,38)	(34,37,39,36)

Figure 1 : Le cube de Rubik

Figure 2 : Le même après une rotation A

2 Dessiner le Cube

Il est demandé de représenter le cube sur écran en montrant les six faces. La réalisation minimale consiste à faire un dessin semblable à ce qui vous est donné dans le texte du projet en y ajoutant la possibilité de représenter des couleurs. Vous pouvez, a votre guise, proposer d'autres dessins et fournir à l'utilisateur de votre programme la possibilité de faire tourner les faces du cubes autant qu 'il le veut.

3 Calculs dans le groupe symetrique

La traduction du problème en termes algébriques est assez simples, on se donne un ensemble de six générateurs A,B,C,D,E,F d' un groupe de permutations sur 48 éléments et on cherche a' decomposer une permutation quelconque comme produit de générateurs. L'inverse de la décomposition cherchée est la suite des rotations à effectuer pour revenir à la position de départ. Des techniques de calcul dans les groupes de permutations ont été établies et on connait des méthodes permettant de répondre à ces questions. Pour cela on construit une matrice T de taille n× n (ici n= 48) dit des générateurs forts, chaque entrée T[i,j] de T est ou bien non définie ou bien une permutationa_i,j qui laisse fixes 1,2,... i-1 et telle que a_i,j(i)= j. La construction de ce tableau se fait par application de la procédure suivante que ces auteurs [sims] ont appelé sift.

On note dans cette procédure par a.b le produit des deux permutations a et b, par identite la permutation identique, par Inverse(x) l'inverse de la permutation x.


procedure Sift(x:Permutation; i : integer);
    var j integer;
    begin
    j := x[i];
    if x <> identite and i<= n then
         if not Defini(T[i,j]) then T[i,j] := x
             else Sift(Inverse(T[i,j]).x,i+1)
    end;

La construction du tableau T se fait alors par un appel répété de la procédure sift comme suit:

Initialiser T[i,j] à indéfini pour tous les I,J
Faire Sift(X,1) pour X= A,B,C,D,E,F
Pour tous les couples T[i,j], T[k,l] définis faire Sift(T[i,j].T[k,l],1) tant que cette procédure ajoute de nouveaux éléments au tableau.

On remarque que cet algorithme de construction du tableau demande n⁶ opérations car Sift(x) demande le calcul de n produits de permutations et de n inverses ce qui prend n² opérations. Dans la programmation de l'algorithme il sera commode de conserver deux versions du tableau T l'une contiendra les permutations sous forme d'un vecteur de taille n contenant pour tout i l'image de i par la permutation, l'autre sous forme d'un produit des générateurs de base. Cette deuxième version sera utile dans la décomposition des opérations sur le cube comme un produit des opérations de base.

Grace à la table T, exprimer une permutation x comme produit de génératuers consiste à appeler la procédure Sift(x,1) et à ecrire successivement les T[i,j] qu'elle calcule. La permutation x appartient au groupe engendré si et seulement si le calcul se termine par un T[i,j] égal à l'identité.

La construction du tableau T est obligatoire pour tous ceux qui choisissent ce projet, ceux qui s'interessent à l'algèbre et l'algorithmique des groupes de permutations pourront tenter d'améliorer les performances de l'algorithme précédent et de réaliser d'autres fonctions sur le groupe symettrique possibles grace à la procédure Sift.

4 Rappel du problème en termes algébriques

On représente une position du cube de Rubik par une permutation de ses 48 facettes, la position initiale est représentée par l'identité et la position décrite par une permutation a est telle que a(i) indique le numéro de la facette où se trouve la facette ayant pour numéro i.¹. Les transformations du cube produites par les rotations des faces sont appelées A,B,C,D,E,F ce sont, toutes les six, des permutations ayant 5 cycles de longueur 4 et 28 points fixes. Si une position P est décrite par la permutation a, la permutation produit a A décrit la position obtenue à partir de P en effectuant la rotation A. Dans cette notation le produit a b désigne la permutation obtenue en effectuant d'abord a puis b:

a b (i) = b(a(i))

Pour connaître la suite de transformations permettant de revenir de la position P (décrite par la permutation a) à la position initiale, il faut décomposer a en un produit ne faisant intervenir que les permutations A,B,C,D,E,F. Si a s'écrit: a = X₁ X₂ ... X_p, la suite des rotations à effectuer pour revenir à la position initiale est, dans cet ordre:

X_p^-1,X_p-1^-1,... X₂^-1,X₁^-1

Noter que, puisque chacune des rotations X est d'ordre 4, on a:

X^-1 =X³

Le problème se pose donc de la façon suivante:

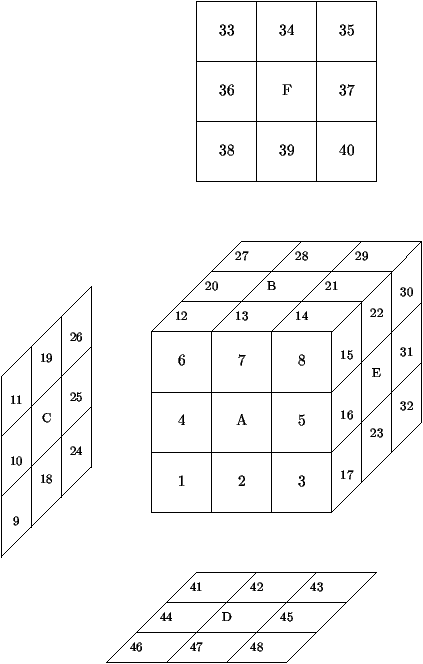
Etant donné un sous groupe G de S₄₈engendré par A,B,C,D,E,F,et une permutation quelconque a déterminer si a appartient au groupe G; et dans le cas positif donner une décomposition de a comme produit des permutations A,B,C,D,E,F.

5 Résultats théoriques

5.1 Table de permutations

Dans ce paragraphe on utilise les notations suivantes: n est un entier positif, G un sous groupe du groupe symétrique de S_n engendré par une famille de permutations X, on écrit G= <X>.

Un tableau de permutations sur n est une table (ou matrice) T possédant n lignes et n colonnes, telle que:

Pour tout i, (1£ i £ n), T[i,i] est la permutation identique notée id,
Pour tout i,j, (1£ i £ n, 1£ j £ n, i¹ j), T[i,j] est ou bien indéfinie ou bien une permutation s telle que:
" k< i s(k) = k, s(i)=j

Remarque. Dans un tel tableau de permutations, on vérifie que T[i,j] est indéfini pour i>j en effet la condition donnée plus haut entraine pour s = T[i,j], i>j:

s(j) = j s(i)=j

et ceci est contradictoire avec le fait que s est une permutation.

Pour un tableau de permutations T on note T_i l'ensemble de toutes les permutations qui se trouvent sur la ligne i et, par abus de langage, on dénote aussi par T l'ensemble des permutations qui se trouvent dans le tableau T. On dira que le tableau T est un tableau de calcul du groupe G si tous les éléments de T appartiennent à G et si de plus G est engendré par les éléments de T. On a ainsi:

<T >= < È_i=1,n T_i> = G

On remarque que les permutations situées sur ligne i>1 fixent au moins i - 1 points; il n'y a pas de condition particulière pour celles qui figurent sur la première ligne sinon que l'image de 1 par celle qui se trouve en colonne j est égale à j.

Exemple. Considérons, pour n=7 le groupe engendré par les deux permutations:

s = (1,2,3,4,5,6,7) a = (2,6)(4,5)

Alors le tableau T donné ci-dessous est un tableau de calcul de G:

id	s	-	-	-	-	-
-	id	-	-	-	a	-
-	-	id	-	-	-	-
-	-	-	id	-	-	-
-	-	-	-	id	-	-
-	-	-	-	-	id	-
-	-	-	-	-	-	id

Dans ce tableau le symbole - désigne l'indéfini.

Proposition: Soit T un tableau de calcul du groupe G et soit pour tout i, i= 1 ... p deux permutations s_i et s' _i appartenant à la même ligne T_i de T alors l'égalité:

s_p s_p-1 ... s₂ s₁ = s'_p s'_p-1 ... s'₂ s'₁

implique s_i = s'_i pour tout i=1,p.

On dit que s_p s_p-1 ... s₂ s₁ est une décomposition de la permutation produit dans le tableau T. On a donc montré que cette décomposition, quand elle existe, est unique.

5.2 La procédure Sift

Lorsqu'on se donne un système de générateurs X d'un groupe G il n'est pas toujours immédiat de construire un tableau de calcul de G. En effet, si par exemple il existe deux permutations a , b de X telles que a(1) = b(1) on ne peut les mettre toutes les deux dans la même position du tableau T. Une technique consiste à remplacer la permutation a par la permutation a b^-1 , le système obtenu engendre le même groupe. Il faut alors mettre a b^-1 (qui fixe le point 1), sur la ligne 2 si la position correspondante n'est pas déjà occupée. Si cette position est déjà occupée on doit réitérer cette technique. On construit ainsi une permutation que l'on note Sift_T(a) et qui est donnée par l'algorithme:


Sift(alpha: permutation):permutation;
    begin
    u := alpha;
    i := 1;
    j := alpha[i];
    while ( i<= n and not(defini(t[i,j])) do
        begin
        u := Produit(u,Inverse(T[i,j]));
        i:= i + 1;
        j := u[i];
        end
    Sift := u;
    end;

On note Sift_T(a) la valeur de la permutation u à la fin de l'algorithme Sift, celle-ci est l'identité si et seulement si la permutation a admet une décomposition ayant la forme donnée plus haut.

5.3 Tableau complet

On dira que le tableau T est un tableau complet de calcul du groupe G, si toute permutation du groupe admet une décomposition de la forme:

s_n s_n-1 ... s₂ s₁

où s_i appartient à la ligne T_i du tableau T. On a alors le résultat suivant:

Proposition. Soit G un groupe engendré par un ensemble X de permutations et T un tableau de calcul de G= <T>, alors les assertions suivantes sont équivalentes:

Le groupe G a un nombre d'éléments égal au produit Õ_i=1ⁿt_i où t_i est le nombre de permutations se trouvant sur la ligne T_i du tableau T.
Pour toute permutation a du groupe G, il existe des permutations s_i, i=1,n, ( où pour tout i, s_i appartient à la ligne T_i du tableau T), telles que: a = s_n s_n-1 ... s₂ s₁.
Pour toute permutation a engendrée par les éléments de T on a Sift_T(a) = id
Pour tout couple x,y d'élément figurant dans T on a: Sift_T(xy) = id

6 Algorithme

De la proposition qui précède on déduit l'algorithme suivant, décrit dans le sujet du projet. On l'exprime ici façon informelle:

Tant qu'il existe un produit xy d'éléments de T tel que Sift_T(xy) ¹ id Ajouter Sift_T(xy) à T.

On remarque que cet algorithme se termine car le nombre de places à l'intérieur du tableau T est limité. Le test d'arrêt consiste à vérifier que tous les produits d'éléments appartenant au tableau ont été calculés et que la procédure Sift leur a été appliquée.

Ainsi dans le pire des cas il y a n(n-1) /2 permutations dans le tableau soit de l'ordre de n²/4 produits à effectuer sur lesquels il faut appliquer la procédure Sift. Cette dernière demande d'évaluer n produits de permutations et n inverses. A chaque fois, cela nécessite de l'ordre de n opérations, ainsi Sift(alpha) demande n² opérations et l'ensemble de l'algorithme a une complexité de n⁶. Ceci est bien grand même si n=48.

A titre d'exemple on peut calculer ce que donne l'algorithme appliqué au groupe défini plus haut. On construit le tableau T suivant:

id	s	s²	s³	s⁴	s⁵	s⁶
-	id	b₁	b₂²	b₂	a	b₃
-	-	id	-	g₁	g₂	g₃
-	-	-	id	-	-	-
-	-	-	-	id	-	-
-	-	-	-	-	id	-
-	-	-	-	-	-	id

Dans ce tableau le symbole - désigne l'indéfini et on a:

b₁= (2,3)(4,7) b₂= (2,5,4,6)(3,7) b₃= (2,7,6)(3,5,4)

g₁ = (3,5)(6,7) g₂= (3,6)(4,7) g₃= (3,7)(5,6)

On calcule l'ordre du groupe en multipliant le nombre d'éléments de chaque ligne ce qui donne 7 × 6 × 4 = 168.

7 Conseils de programmation

Il est bon de connaître deux versions du tableau T, l'une où chaque case contient une permutation sous la forme d'un vecteur indiquant pour tout i=1,n l'image de chaque élément i, l'autre sous la forme d'une chaîne de caractères la représentant comme produit des générateurs. Dans la représentation sous forme de chaîne de caractères il peut être intéressant de simplifier par la relation X⁴ = id pour X = A,B,C,D,E,F.
Il faudra veiller à mettre régulièrement à jour une information sur les produits d'éléments de T qui auront été effectués et pour lesquels la procédure Sift a été appliquée.
Il faut faire preuve d'une certaine imagination pour tenter de trouver des techniques permettant de donner des permutations dans le tableau T s'exprimant avec peu de symboles A,B,C,D,E,F .

1: et non pas le numéro de la facette qui se trouve en position i, comme cela est indiqué par erreur dans le texte du projet

Ce document a été traduit de L^AT_EX par H^EV^EA.