Interprétation (environnements)
-
A
- Un petit tour autour du point fixe.
- B
- De l’évaluaton à l’interprétation : environnements.
- C
- Interprétation par valeur.
Point fixe et réduction
On s’intéresse aux « solutions » d’équations du genre :
| x =s t, avec x variable, et t terme de PCF où x apparaît.
|
« =s » est l’égalité dans la sémantique.
Soit u = Fix x -> t avec
C’est-à-dire, inventons le point fixe explicite.
On pose l’exigence sémantique t—→t′ ⇒ t =s t′.
Il est alors évident que u est solution de x =s t.
Point fixe construit
Une première étape : « abstraire x dans t ».
| x = (Fun y -> t′) x, avec t′ = [y\x]t.
|
-
On a trivialement (Fun y -> t′) x—→t.
- Il apparaît clairement que l’on recherche le point-fixe (x = Φ x)
d’une fonction Φ = Fun y -> t′.
Soit un terme u tel que u—→*Φ u—→[u\y]t′,
Soit en fait (car t′ = [y\x]t) :
C’est à dire que u est solution.
Construction explicite
De u tel que u ←→* Φ u.
Soit la fonction suivante curry :
Fun f -> (Fun x -> f (x x)) (Fun x -> f (x x))
On va montrer que pour tout terme Φ :
(←→* fermeture
réflexive-symétrique-transitive de —→, entraîne =s).
Démonstration de curry Φ ←→*
Φ (curry Φ)
Posons v = Fun x -> f (x x)
Par une β-réduction il vient :
Lemme :
t—→t′ ⇒ [u\x]—→[u\x]t′
Donc : [Φ\f](v v)—→[Φ\f]f (v v). (1)
Or (une β) : curry Φ—→[Φ\f](v v) (2)
Et c’est fini :
curry Φ
—→
[Φ\f](v v)
—→
[Φ\f](f (v v))
=
Φ ([Φ\f](v v))
←—
Φ (curry Φ)
|
Astuce ultime
Notons F = Fix x -> t.
On effectue les substitution de x dans t, dès que prêt :
| F
→
[F\x]t
→
[[F\x]t\x]t
→
[[[F\x]t\x]t\x]t
→ …
|
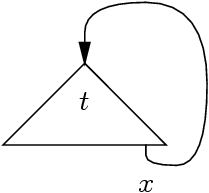
On obtient un terme « infini »,
représentable par un graphe :
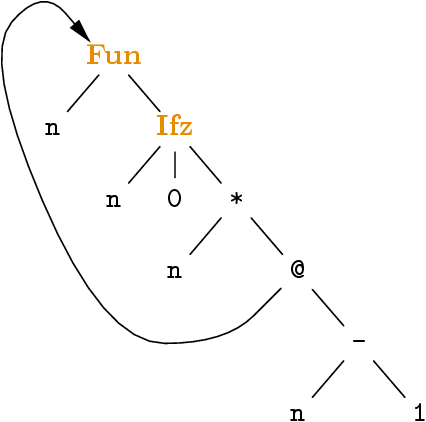
Plus clair sur un exemple
Fabriquer un tel graphe
-
En Caml, une définition récursive !
let rec pcf_fact =
Fun ("n",
Ifz (Var "n", Num 0,
Op (Mul,Var "n",
App (pcf_fact,Op (Sub,Var "n",Num 1)))))
- En Java/langage machine : modification d’un terme.
Pcf node =
new App (null, new Op(Sub, new Var ("n"), new Num (1))) ;
Pcf top = new Fun("n",new Ifz (…)) ;
node.left = top
Environnements
Appel par nom
| t1↪nFun x -> t3 [t2\x]t3↪nv |
|
| t1 t2↪nv |
|
| |
| [t1\x]t2↪nv |
|
| Let x = t1 In t2↪nv |
|
| | [(Fix x -> t)\x]t↪nv |
|
| Fix x -> t↪nv |
|
|
| t1↪n0 t2↪nv |
|
| Ifz t1 Then t2 Else t3↪nv |
|
| | t1↪nn (n ≠ 0) t3↪nv |
|
| Ifz t1 Then t2 Else t3↪nv |
|
| | t1↪nn1 t2↪nn2 |
|
| t1 op t2↪nn1 op n2 |
|
| |
Appel par valeur
| t1↪vFun x -> t3
t2↪vv2 [v2\x]t3↪vv |
|
| t1 t2↪vv |
|
| |
| t1↪vv1 [v1\x]t2↪vv |
|
| Let x = t1 In t2↪vv |
|
| | [(Fix x -> t)\x]t↪vv |
|
| Fix x -> t↪vv |
|
|
| t1↪v0 t2↪vv |
|
| Ifz t1 Then t2 Else t3↪vv |
|
| | t1↪vn (n ≠ 0) t3↪vv |
|
| Ifz t1 Then t2 Else t3↪vv |
|
| | t1↪vn1 t2↪vn2 |
|
| t1 op t2↪vn1 op n2 |
|
| |
Substitution (dans un évaluateur)
Pour évaluer (Fun x -> t1) t2,on calcule [t2\x]t1
(ou [v2\x]t1)
Si t2 n’a pas de variable libre, alors la substitution est simplifiée :
| [t2\x](Fun x -> t1) = Fun x -> t1
|
| | [t2\x](Fun y -> t1) = Fun y -> [t2\x]t1
|
|
Et c’est tout, car y n’est certainement pas libre dans t2 .
Toutefois,
-
La substitution reste chère (copie de termes).
- Les corps de fonctions sont transformés (ce qui éloigne
du modèle où les fonctions sont du code).
On veut mélanger évaluation et substitution, comme on avait mélangé
recherche de radical et réduction.
Substitution
Pour évaluer (Fun x -> (x * x) + x) 4
— noté (Fun x -> t) 4.
| (Fun x -> t)↪n(Fun x -> t) |
|
| |
|
|
| (Fun x -> t) 4↪n20 |
|
|
-
Évaluer Fun x -> t.
- Effectuer la substitution [4\x]t,
ce qui donne (4 * 4) + 4.
- Et un peu d’arithmétique (calculer (4 * 4) + 4).
Une alternative
-
Garder la définition x = 4 dans un environnement.
- Évaluer le terme ouvert dans cet environnement,
noté E ⊢ t↪v.
| [x = 4] ⊢ x↪4
[x = 4] ⊢ x↪4 |
|
| [x = 4] ⊢ (x * x)↪16 |
|
[x = 4] ⊢ x↪4 |
|
|
| [x = 4] ⊢ (x * x) + x↪20 |
|
|
- La règle nouvelle étant du genre
- Cela revient à retarder la substitution, jusqu’à l’évaluation du
corps de la fonction.
Priorité (à droite)
Valeur de Let x = 4 In Let x = 5 In x ?
En toute rigueur
| [5\x]x↪n5 |
|
| Let x = 5 In x↪n5 |
|
|
|
[4\x](Let x = 5 In x)↪n5
|
|
|
| Let x = 4 In Let x = 5 In x↪n5 |
|
|
-
Effectuer [4\x](Let x = 5 In x),
soit Let x = 5 In x.
-
Effectuer [5\x]x, soit 5.
- Évaluer le résultat (qui est en forme normale).
- En gros, on a calculé
[4\x]([5\x]x).
Priorité avec les environnements
Un environnnement contient maintenant plusieures définitions
x=n, et on applique la priorité.
| [x = 4, x = 5] ⊢ x↪5 |
|
| [x = 4] ⊢ Let x = 5 In x↪5 |
|
|
| ⊢ Let x = 4 In Let x = 5 In x↪5 |
|
|
-
Évaluer Let x = 5 In x dans l’env. [x = 4].
- Évaluer x dans l’env. [x = 4, x = 5].
- Ce qui nous donne 5 qui est une valeur.
- Les définition de l’env. sont à considérer dans l’ordre.
Formalisation de la liaison lexicale
On pourrait écrire :
| | […] ⊢ x↪n |
|
| […, y=ny] ⊢ x↪n |
|
|
| […, x=n] ⊢ t↪v |
|
| […] ⊢ Let x = n In t↪v |
|
|
On préfère une notation plus abstraite.
| | E ⊕ [x = n] ⊢ t↪v |
|
| E ⊢ Let x = n In t↪v |
|
|
Les environnements sont des fonctions des variables.
Avec un opérateur ⊕ défini par
Avec de bêtes listes d’associations :
type 'a env = (Var.t * 'a) list
Opération « ⊕ ».
(* Ajouter l'association de x à t *)
let add x t env = (x,t)::env
Recherche :
let rec find x env = match env with
| [] -> raise (Error ("Variable libre : " ^ x))
| (y,t)::env -> if x=y then t else find x env
(C’est List.assoc).
La priorité à droite devient la priorité à gauche :
find x ((x,t1)::(x,t2)::…) → t1
Mais c’est pareil.
Exemples
Généralisons les définitions des environnements : [x = t]
(et non plus slt [x=n]).
-
On interprète Let y = 4 + 5 In y + 3
dans l’env. vide.
- On interprète y + 3 dans [y = (4 + 5)].
- On interprète y dans [y = (4 + 5)].
- On interprète 4 + 5 dans… peu importe : terme clos.
Recommençons.
-
On interprète Let y = 4 + x In y + 3
dans [x = 5].
- On interprète y + 3 dans [x = 5, y = (4 + x)].
- On interprète y dans [x = 5, y = (4 + x)].
- On interprète 4 + x dans … [x = 5] ?
Le glaçon (thunk)
Dans l’exemple précédent,
nous avons négligé la définition de la substitution.
-
On interprète Let y = 4 + x In y + 3
dans [x = 5].
Donc on considère
| [5\x](Let y = 4 + x In y + 3)
|
C’est-à-dire
| Let y = [5\x](4 + x) In [5\x](y + 3)
|
Principe de l’interprétation = ne pas substituer par avance.
Donc, les environnements contiennent des applications de substitutions
retardées : des glaçons, notés <t•E>.
Reprenons
Le terme clos 5 se représente facilement comme le glaçon
<5•[]>
-
On interprète Let y = 4 + x In y + 3
dans [x = <5•[]>].
- On interprète y + 3 dans [x = <5•[]>,
y = <4 + x•[x = <5•[]>]>].
- On interprète y dans [x = <5•[]>,
y = <4 + x•[x = <5•[]>]>].
-
Et donc on évalue 4+x dans l’environnement
[x = <5•[]>].
- Ce qui finira par donner 9
- Ce qui finira par donner 9 + 3 et donc 12.
Les règles de l’interprétation
Sachant que l’environnement lie des variables à des glaçons, qui
sont eux-mêmes des paires « terme × environnement ».
Deux règles « faciles »
| E(x) = <t•E′> E′ ⊢ t↪v |
|
| E ⊢ x↪v |
|
| | E ⊕ [x = <t1•E>] ⊢ t2↪v |
|
| E ⊢ Let x = t1 In t2↪v |
|
|
Mais aussi, bien évidemment, l’arithmétique un peu aménagée.
| | E ⊢ t1↪n1 E ⊢ t2↪n2 |
|
| E ⊢ t1 op t2↪n1 opn2 |
|
|
La conditionnelle pareillement aménagée.
| E ⊢ t1↪0 E ⊢ t2↪v |
|
| E ⊢ Ifz t1 Then t2 Else t3↪v |
|
| | E ⊢ t1↪n (n ≠ 0) E ⊢ t3↪v |
|
| E ⊢ Ifz t1 Then t2 Else t3↪v |
|
|
Et le point fixe pareillement aménagé.
| E ⊕ [x = <Fix x -> t•E>] ⊢ t↪v |
|
| E ⊢ Fix x -> t↪v |
|
|
Fermeture
Nous avions la règle d’évaluation des fonctions
Quelle peut-être la règle d’interprétation ?
On a très envie de dire <Fun x -> t•E>, mais cela compliquerait
exagérément le concept de valeur. On définit plutôt la
fermeture <x•t•E> comme ce glaçon là.
Nouvelle règle de l’application.
| E ⊢ t1↪<x•t′1•E′>
E′ ⊕ [x = <t2•E>] ⊢ t′1↪v |
|
| E ⊢ t1 t2↪v |
|
|
NB : Les valeurs ne sont plus des termes.
Impact de la fermeture
Quelle est la valeur du terme
Let x = 4 In
Let f = Fun y -> y + x In
Let x = 5 In
f x
Le point crucial est de savoir à quoi se rapporte x
dans y + x.
À la définition de x active au moment de la définition
de f (et non pas de son application).
Et donc le résultat est 9 (et non pas 10).
La fermeture est ici cruciale, f est liée au glaçon
| <Fun y -> y + x•[x=<4•[ ]>]>
|
Dont la valeur est la fermeture : <y•y + x•[x=<4•[ ]>]>.
Et y + x s’évalue dans
[x=<4•[ ]>, y = <x•[…,x =
<5•⋯>]>].
| [x = …, f = …, x = <5•[…]>] ⊢ f 5↪10
|
|
| [x=…, f=
<Fun y -> y + x•[x=<4•[ ]>]>] ⊢ Let x = 5 In ⋯↪10 |
|
|
| [x = <4•[ ]>] ⊢ Let f = Fun y -> y + x In ⋯↪10 |
|
|
| ⊢ Let x = 4 In ⋯↪10 |
|
|
Les valeurs v sont des entiers n ou des fermetures <x•t•E>.
Les environnements E lient les variables x à des glaçons <t•E>.
| | E ⊢ t1↪n<x•t′1•E′>
E′ ⊕ [x = <t2•E>] ⊢ t′1↪nv |
|
| E ⊢ t1 t2↪nv |
|
|
| E ⊕ [x = <Fix x -> t•E>] ⊢ t↪nv |
|
| E ⊢ Fix x -> t↪nv |
|
|
| E(x) = <t•E′> E′ ⊢ t↪nv |
|
| E ⊢ x↪nv |
|
| | E ⊕ [x = <t1•E>] ⊢ t2↪nv |
|
| E ⊢ Let x = t1 In t2↪nv |
|
|
| | E ⊢ t1↪nn1 E ⊢ t2↪nn2 |
|
| E ⊢ t1 op t2↪nn1 opn2 |
|
|
| E ⊢ t1↪n0 E ⊢ t2↪nv |
|
| E ⊢ Ifz t1 Then t2 Else t3↪nv |
|
| | E ⊢ t1↪nn (n ≠ 0) E ⊢ t3↪nv |
|
| E ⊢ Ifz t1 Then t2 Else t3↪nv |
|
|
Interpréter par valeur
Notable simplification
Les règles de l’évaluation par valeur.
| t1↪vFun x -> t3
t2↪vv2
[v2\x]t3↪vv |
|
| t1 t2↪vv |
|
| | t1↪vv1 [v1\x]t2↪vv |
|
| Let x = t1 In t2↪vv |
|
|
Les substitutions retardées sont de la forme [v\x]⋯
Comme v est n (entier) ou <x•t•E> (fermeture),
plus besoin de glaçon.
Malheureusement, il y a la récursion.
| [(Fix x -> t)\x]t↪vv |
|
| Fix x -> t↪vv |
|
|
Interprétation par valeur, simplicité ?
Récursion avec environnement (et glaçon) :
| E ⊕ [x = <Fix x -> t•E>] ⊢ t↪vv |
|
| E ⊢ Fix x -> t↪vv |
|
|
Donc : les environnements lient des variables à des valeurs v,
ou à des glaçons de la forme <Fix x -> t•E> (exclusivement).
Deux règles pour les variables au lieu d’une.
| | E(x) = <Fix x -> t•E′> E′ ⊢ Fix x -> t↪vv |
|
| E ⊢ x↪vv |
|
|
Et changer les règles de l’application et du Let.
| E ⊢ t1↪v<x•t′•E′>
E ⊢ t2↪vv2
E′ ⊕ [x = v2] ⊢ t′↪vv |
|
| E ⊢ t1 t2↪vv |
|
|
| E ⊢ t1↪vv1
E ⊕ [x = v1] ⊢ t2↪vv |
|
| E ⊢ Let x = t1 In t2↪vv |
|
|
Et c’est tout, mais il est dommage d’avoir des glaçons,
juste pour coder la récursion.
Les valeurs v sont des entiers n ou des fermetures <x•t•E>.
Les environnements E lient les variables x à des valeurs v
ou à des glaçons de la forme <Fix x -> t•E>.
| | E(x) = <Fix x -> t•E′> E′ ⊢ Fix x -> t↪vv |
|
| E ⊢ x↪vv |
|
|
| E ⊢ t1↪v<x•t′•E′>
E ⊢ t2↪vv2
E′ ⊕ [x = v2] ⊢ t′↪vv |
|
| E ⊢ t1 t2↪vv |
|
| | E ⊢ t1↪vv1
E ⊕ [x = v1] ⊢ t2↪vv |
|
| E ⊢ Let x = t1 In t2↪vv |
|
|
| E ⊕ [x = <Fix x -> t•E>] ⊢ t↪vv |
|
| E ⊢ Fix x -> t↪vv |
|
|
| | E ⊢ t1↪vn1 E ⊢ t2↪vn2 |
|
| E ⊢ t1 op t2↪vn1 opn2 |
|
|
| E ⊢ t1↪v0 E ⊢ t2↪vv |
|
| E ⊢ Ifz t1 Then t2 Else t3↪vv |
|
| | E ⊢ t1↪vn (n ≠ 0) E ⊢ t3↪vv |
|
| E ⊢ Ifz t1 Then t2 Else t3↪vv |
|
|
Une remarque
En appel par valeur, Fix sert surtout à définir des fonctions.
Let fact =
Fix f Fun x -> Ifz x Then 1 Else x * f (x - 1) In
…
Interprétation de Fix f -> Fun x -> t,
noté FixFun f x -> t
| E ⊕ [f = <FixFun f x -> t•E>] ⊢ Fun x -> t↪<x•t•E′> |
|
|
| E ⊢ Fix f -> Fun x -> t↪<x•t•E′> |
|
|
Avec
| E′ = E ⊕ [f = <FixFun f x -> t•E>]
|
Première variante
Si Fix f -> ⋯ est nécessairement de la forme
FixFun f x -> t, on peut remplacer les glaçons par une forme
particulière de fermeture.
La nouvelle fermeture <f•x•t•E>,
qui
représente la fermeture à trois composants de la forme
| <x•t•[f = <FixFun f x -> t•E>]> |
On pose alors directement.
| E ⊢ FixFun f x -> t↪v<f•x•t•E> |
|
|
On a alors une règle supplémentaire pour appliquer
les nouvelles fermetures…
| E ⊢ t1↪v<f•x•t•E′>
E ⊢ t2↪vv2
E′ ⊕ [f = <f•x•t•E′>, x=v2] ⊢ t↪vv |
|
| E ⊢ t1 t2↪vv |
|
|
Astuce
Si on représente une fermeture à trois composantes
<x•t•E> comme une fermeture à quatre composantes
<_f•x•t•E>, alors
la nouvelle règle d’application des fermetures remplace l’ancienne !
On pose donc :
| _f ∉F(t) |
|
| E ⊢ Fun x -> t↪v<_f•x•t•E> |
|
|
Et on supprime l’ancienne règle d’application.
| E ⊢ t1↪v<x•t′•E′>
E ⊢ t2↪vv2
E′ ⊕ [x = v2] ⊢ t′↪vv |
|
| E ⊢ t1 t2↪vv |
|
|
Mais c’est bien artificiel (liaison de _f inutile).
Revenons à l’interprétation de t = FixFun f x -> b (page 33)
| |
|
| E ⊕ [f = g] ⊢ Fun x -> b↪v<x•b•E ⊕ [f = g]> |
|
|
| E ⊢ FixFun f x -> b↪v<x•b•E ⊕ [f = g]> |
|
|
Où g note le glaçon <FixFun f x -> b•E>.
Anticipons maintenant l’interprétation de g. Une fois
Et encore une fois
| <x•b•E ⊕ [f = <x•b•E ⊕ [f = g]>]>
|
Etc. on obtient une fermeture ordinaire, mais bouclée, avec :
Un graphe
Encore plus fort
Soit un interpréteur (qui est au final un programme)
Reste à construire le graphe, pour interpréter FixFun f x -> b
dans l’env. E, par ex. en Caml.
type value = (* Les valeurs *)
| Integer of int | Closure of Var.t * Ast.t * env
and env = (Var.t * value) list (* les environnements *)
let rec inter E t = match t with
…
| Fix (f,Fun (x,b)) ->
let rec clo = Closure (x, b, (f,clo)::E) in
clo
Avantage définitif : une seule sorte de fermeture.
-
TP, divers interpréteurs.
- La prochaine fois, compilation.
Ce document a été traduit de LATEX par HEVEA