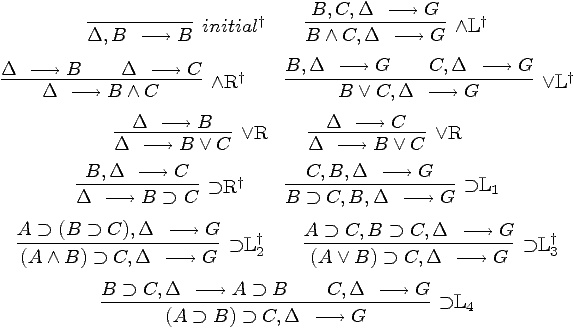Caml types and intuitionistic logic
A project by Dale Miller
Dale.Miller @ inria.fr
1 Goal
The goal of this project is to use a theorem prover for propositional
intuitionistic logic in order to answer questions about a collection
of Caml types. In particular, if one is given a list of Caml types (none
of which are polymorphic) and a particular ``target'' type, one would
like to know if it is possible to build a ``simple'' Caml program of
that target type from that list of types.
2 Background
By simple Caml program over Δ, we shall mean an Caml program
built from constants in Δ using just application, abstraction, and
the constructors for conjunction and disjunction. Here, conjunction
is specified using the conj type and disjunction is specified
using the disj type.
# type ('a,'b) conj = Pair of 'a * 'b;;
type ('a, 'b) conj = Pair of 'a * 'b
# let left = function (Pair(x,y)) -> x;;
val left : ('a, 'b) conj -> 'a = <fun>
# let right = function (Pair(x,y)) -> y;;
val right : ('a, 'b) conj -> 'b = <fun>
# type ('a,'b) disj = Putl of 'a | Putr of 'b;;
type ('a, 'b) disj = Putl of 'a | Putr of 'b
# let cases = function (Putl x,f,g) -> f x | (Putr x,f,g) -> g x;;
val cases : ('a, 'b) disj * ('a -> 'c) * ('b -> 'c) -> 'c = <fun>
#
Notice that it is possible to use simple Caml programs as proofs of
propositional formulas. Consider, for example, the following Caml
programs.
(* Prove: ((a or b) -> c) -> a -> c *)
# let p1 x y = (x (Putl y));;
val p1 : (('a, 'b) disj -> 'c) -> 'a -> 'c = <fun>
(* Prove: ((a -> b) and (a -> c)) -> a -> (b and c) *)
# let p2 x y = Pair ((left x) y,(right x) y);;
val p2 : ('a -> 'b, 'a -> 'c) conj -> 'a -> ('b, 'c) conj = <fun>
(* Prove: (a and b) -> (b and a) *)
# let p3 x = Pair(right x, left x);;
val p3 : ('a, 'b) conj -> ('b, 'a) conj = <fun>
(* Prove: (a or b) -> (b or a) *)
# let q1 x = cases(x, (fun y -> (Putr y)),(fun y -> (Putl y)));;
val q1 : ('a, 'b) disj -> ('b, 'a) disj = <fun>
(* Prove: (a or b) -> (a -> c) -> (b and d -> c) -> d -> c *)
# let q2 x y z w = cases(x, (fun n -> (y n)),
(fun m -> (z (Pair(m,w)))));;
val q2 : ('a, 'b) disj -> ('a -> 'c) ->
(('b, 'd) conj -> 'c) -> 'd -> 'c = <fun>
#
Thus, for example, the Caml code q2 can be seen as a proof of the
formula propositional formula
(a∨ b)⊃ (a⊃ c)⊃ ((b∧ d)⊃ c)⊃
d⊃ c,
where ⊃ denotes implication (replaces the
function space arrow -> and where ∨ and ∧ denote
disjunction and conjunction (respectively). (Notice that ⊃
and -> both associate to the right.) The proof described by
q2 might be read as follows: Assume that we are given the four
formulas a∨ b, a⊃ c, (b∧ d)⊃ c,
d
and try to prove c. We need to do a case analysis: if a is
true, then, using the second displayed formula, we conclude c
immediately. In the other case where b is true, we first must
conclude b∧ d (since d is given as the fourth formula above)
and then, using the third formula, we can conclude c also. Thus, in
either case, we have established c. Notice that the structure of
q2 is rather similar to the structure of this informal proof.
This connection between types and formulas is often called the
Curry-Howard Isomorphism.
3 Allowing other typed constants
Now consider the problem of having a library of Caml programs for which
you have easy access to their types. (We shall assume that this
library does not contain constants of polymorphic type.) For example,
assume you have the
following typed symbols:
type f : int -> list bool
type g : list int -> int -> int
type h : (bool -> int) -> list bool -> list int
type u : bool -> int
type v : (int, real) or -> complex
type m : string -> int
type n : string -> real
One might try to use your solution to this project to answer the
following questions: Is there a term of type int -> list int?
Of type list int -> int? Of type string -> complex? Of type
complex -> string? Etc.
Given the discussion before, all of these questions have a parallel in
logic. For example, given the propositional formulas
int ⊃ listbool
listint ⊃ int ⊃ int
(bool ⊃ int) ⊃ listbool ⊃ listint
bool ⊃ int
(int ∨ real) ⊃ complex
string ⊃ int
string ⊃ real
is it possible to prove the formula string⊃ complex?
(Notice also that (list bool) is treated as a propositional symbol
listbool.) If there is a proof, the proof should describe a simple Caml
program. If there is no such proof, then there is no such program.
This formal connection is part of the theory of the Curry-Howard
Isomorphism.
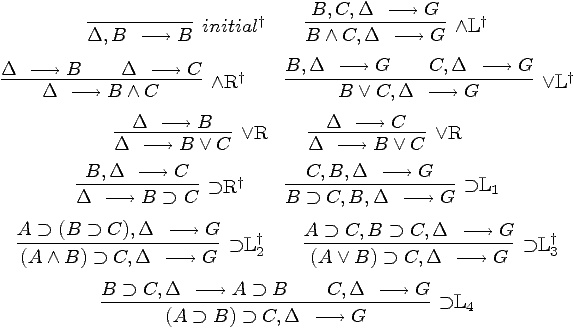
Figure 1 : Inference rules in sequent style for propositional logic
[
Dyc92]. The rule ⊃L
1 has the
additional requirement that the formula
B is a
propositional symbol.
4 A proof system for propositional intuitionistic logic
Thus, to answer the questions about whether or not a simple Caml program
of a given type can exist given a collection of (non-polymorphic) Caml
constants, we can instead try to answer the questions whether or not a
given propositional formula follows from a set of other propositional
formulas using the rules for intuitionistic logic. Provability of
propositional intuitionistic logic has been well studied. Provability
is known to be decidable.
A common way to present a proof system for a logic is to use sequent
calculus. For this project, we assume that a sequent is a pair,
written as Δ —→ G where G is a propositional formula and
Δ is a multiset of propositional formulas. [Recall that
a multiset is a set in where objects have a multiplicity:
equivalently, they are list structures in which order does not
matter.] A sequent Δ —→ G denotes, in a sense, the attempt
to proved the formula G from the formulas in Δ: if you will,
consider doing a mathematical proof where at the top of your paper you
write the assumptions (here, Δ) and at the bottom, the statement
you would like to proved from these assumption (here, G).
A sequent calculus proof system for this logic is given
Figure 1 and is due to R. Dyckhoff [Dyc92].
Consider using these rules to search for a proof in intuitionistic
logic. That is, think of starting with a given sequent, consider what
inference rule could give rise to that sequent. Generally, such an
inference rule will give rise to one or two additional sequents that
need to be proved as well. The entire proof search process terminates
when all remaining sequents are justified by the initial rule.
In Figure 1, a few inference rules are marked with a dag
. This means that the conclusion of this inference rule is
provable if and only if the premises are provable. Thus, for
the purpose of searching for a proof, one does not need to backtrack
on the selection of these rules: if they can apply, then apply them
and consider no other choice of inference rule. All other rules may
require backtracking.
5 The actual project
Please implement in a high-level language (preferably Caml, OCaml, or
Java) the following steps.
-
Build a lexical analyzer and parser that will read a collection
of typed Caml constants (a signature) denoting Γ and another Caml
type denoting A.
- Implement the proof search mechanism described by the sequent
system in Figure 1 for the sequent Γ —→ A.
- Report your answer to the user: that is, tell the user whether
or not a simple Caml program of type A exists using constants in the
list Γ.
- If an such an Caml program exists, print out one.
- Develop a good example illustrating the usefulness of your
system.
Références
- [Dyc92]
-
Roy Dyckhoff.
Contraction-free sequent calculi for intuitionistic logic.
Journal of Symbolic Logic, 57(3):795--807, September 1992.
Ce document a été traduit de LATEX par
HEVEA.