| ⋆⋆⋆ |
Question 1. Simuler la compilation. Pour chacune des définitions de méthode ci-dessous, indiquer si elle est acceptée par le compilateur ou non. Si non, dire pourquoi (en moins d'une ligne). Si oui, commenter rapidement sur le sens de la fonction définie, par exemple sur sa terminaison.
a)
public static int f1(int y){
if (y <= 0)
return 1;
else
return f1(y-1) * y;
}
| Correct, calcule la factorielle. |
b)
public static int f2(int y){
return y * f2(y-1);
}
| Cette méthode est acceptée par le compilateur, mais son exécution ne termine pas. |
c)
public static void f3(int y){
return 3*y + 2;
}
| Incorrect, la fonction est déclarée de type void mais elle retourne un entier. |
d)
public static void f4(int y){
if (y == 0)
y = 1;
else
y *= y-1;
}
| Accepté à la compilation, mais ne fait pas grand chose à l'exécution. |
e)
public static int[] f5(int y){
int[] t = int[y];
for (int i = 0; i < y; ++i)
t[i] = i;
return t;
}
| Incorrect, il manque le new dans l'allocation du tableau à la deuxième ligne |
f)
public static int f6(int y){
if (y % 2 == 1)
return 3*y + 1;
return y/2;
}
| Correct, la terminaison est évidente. |
Question 2. Simuler l'exécution.
Vous devez simuler l'exécution de la méthode main ci-dessous. Cette méthode comporte diverses instructions d'affichage. Pour chacune d'elles, précisez ce qui est affiché. Si, pour une raison quelconque, l'affichage n'a pas lieu, précisez pourquoi.[4cm]
class Pale{
public static int f(int y) {
int x = y + 2;
return y;
}
public static void g(int x) {
x = x + 3;
}
public static int h(int y) {
int x = y + 4;
return x;
}
public static void
main(String[] args) {
int x = 2;
x = f(x);
System.out.println(x);
a) Quelle est la valeur affichée par l'instruction précédente ?
| 2 |
x = 2;
g(x);
System.out.println(x);
b) Quelle est la valeur affichée par l'instruction précédente ?
| 2 |
x = 2;
x = h(x);
System.out.println(x);
c) Quelle est la valeur affichée par l'instruction précédente ?
| 6 |
x = 0;
int j;
for (j = 0; j < 4; j++)
x += j;
System.out.println(j);
d) Quelle est la valeur affichée par l'instruction précédente ?
| 4 |
System.out.println(x);
e) Quelle est la valeur affichée par l'instruction précédente ?
| 6 |
for (j = 0; j < 4; j++)
j += j;
System.out.println(j);
f) Quelle est la valeur affichée par l'instruction précédente ?
| 7 |
x = 1;
j = 1;
while (j < 10)
x *= j;
System.out.println(x);
g) Quelle est la valeur affichée par l'instruction précédente ?
| Cette instruction n'est pas atteinte, la boucle précédente ne terminant jamais. |
} }
Question 3. Soit une classe usuelle des cellules de liste (d'entiers) :
class Liste {
int contenu; Liste suivant;
Liste(int x, Liste a) { contenu = x; suivant = a; }
}
Et soit la classe de test suivante.
class TestListe {
public static Liste f1(Liste l){
for ( ; l.suivant != null; l = l.suivant)
;
return l;
}
public static Liste f2(Liste l){
for ( ; l != null; l = l.suivant)
;
return l;
}
…Il s'agit ensuite de simuler l'exécution de la méthode main de la classe TestListe
public static void main(String[] a) {
Liste L = null;
L = new Liste(1, L);
L = new Liste(2, L);
L = new Liste(3, L);
L = new Liste(4, L);
Liste p = f1(L);
System.out.println(p.contenu);
a) Quelle est la valeur affichée par l'instruction précédente ?
| 1 |
System.out.println(L.contenu);
b) Quelle est la valeur affichée par l'instruction précédente ?
| 4 |
p.suivant = new Liste(5, p.suivant);
p = new Liste(6, p);
p.suivant = new Liste(7, p);
System.out.println(p.contenu);
c) Quelle est la valeur affichée par l'instruction précédente ?
| 6 |
p = f2(L);
System.out.println(p.contenu);
d) Quelle est la valeur affichée par l'instruction précédente ?
| Quand elle termine, la fonction f2 renvoie
toujours null.
Le programme doit donc échouer ici, une exception
(NullPointerException ou approchant) étant levée. On considère toutefois que les questions suivantes appellent une réponse. |
p = f1(L);
System.out.println(p.contenu);
e) Quelle est la valeur affichée par l'instruction précédente ?
| 5 |
p.suivant = new Liste(8, p);
p = f1(L);
System.out.println(p.contenu);
f) Quelle est la valeur affichée par l'instruction précédente ?
| La liste pointée par p est bouclée et l'appel à f1 ne termine pas. |
} }
Nous commençons par définir une classe des rectangles.
class Rectangle{
int xmin, xmax, ymin, ymax;
Rectangle(int x, int X, int y, int Y) {
xmin = x; xmax = X; ymin = y; ymax = Y;
}
}
Un objet de la classe Rectangle représente le rectangle [xmin, xmax]×[ymin, ymax]. On définit également une classe pour les listes de rectangles.
class ListeRectangle{
Rectangle contenu;
ListeRectangle suivant;
ListeRectangle(Rectangle x, ListeRectangle a) {
contenu = x; suivant = a;
}
}
Question 4. Écrire une méthode dynamique de la classe Rectangle
boolean estDansRectangle(int x, int y)
qui rend compte de ce que le point de coordonnées (x,y) est à l'intérieur du rectangle ou pas (on considérera que les bords d'un rectangle sont aussi à l'intérieur).
|
boolean estDansRectangle(int x, int y) {
return
(xmin <= x && x <= xmax) &&
(ymin <= y && y <= ymax) ;
} |
Question 5. Écrire une méthode statique
static boolean estDansRectangles(int x, int y, ListeRectangle l)
qui rend compte de ce que le point de coordonnées (x,y) est à l'intérieur d'au moins un des rectangles de la liste l ou pas.
|
static boolean estDansRectangles(int x, int y, ListeRectangle l) {
for ( ; l != null ; l = l.suivant) {
if (l.contenu.estDansRectangle(x, y)) return true ;
}
return false ;
} |
Question 6. Écrire une méthode statique
static int taille(ListeRectangle l)
qui renvoie le nombre de rectangles dans une liste de rectangles.
|
static int taille(ListeRectangle l) {
int r = 0 ;
for ( ; l != null ; l = l.suivant) { r++ ; }
return r ;
} |
Question 7. Écrire une méthode statique
static int[] abcisses(ListeRectangle l)
qui prend en argument une liste de n rectangles et renvoie un tableau contenant les 2n abcisses xmin ou xmax des rectangles de la liste.
|
static int[] abcisses(ListeRectangle l) {
int [] r = new int [2*taille(l)] ;
int i = 0 ;
for ( ; l != null ; l = l.suivant) {
r[i] = l.contenu.xmin ; i++ ;
r[i] = l.contenu.xmax ; i++ ;
}
return r ;
} |
Nous allons maintenant organiser les ensembles de rectangles du plan selon une structure d'arbre binaire représentant le découpage d'un intervalle [XMIN, XMAX] en sous-intervalles. Pour cela, on utilise un arbre binaire dont on veut qu'il possède les propriétés suivantes :
On utilisera la classe suivante:
class Arbre{
static int XMIN; // l'extremite gauche de l'intervalle
static int XMAX; // l'extremite droite de l'intervalle
final static int NOEUD = 1, FEUILLE = 0;
int nature; // Vaut NOEUD ou FEUILLE
int valeur; // Valide pour NOEUD
Arbre filsGauche, filsDroit; // Valide pour NOEUD
ListeRectangle contenu; // Valide pour NOEUD et FEUILLE
Arbre() { nature = FEUILLE; contenu = null; }
Arbre(int v, Arbre fg, Arbre fd){
nature = NOEUD; valeur = v;
filsGauche = fg; filsDroit = fd; contenu = null;
}
}
On associe un intervalle à chaque sommet de l'arbre (y compris aux feuilles) de la manière suivante :
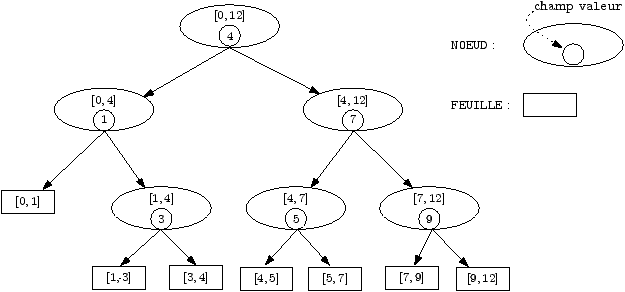
Par exemple dans la figure 1, XMIN vaut 0, XMAX vaut 12 et l'intervalle [0,12] est découpé suivant les valeurs 1, 3, 4, 5, 7 et 9. L'intervalle [0,12] est associé à la racine, l'intervalle [0, 4] à son fils gauche, l'intervalle [4, 12] à son fils droit, et ainsi de suite comme indiqué sur la figure.
La valeur d'un nœud interne de l'arbre est utilisée pour subdiviser l'intervalle qui lui est associé pour obtenir les intervalles associés à ses fils. Toutefois, les bornes de l'intervalle associé à un sommet ne sont pas données explicitement; ainsi sur la figure, le fils gauche de la racine a pour valeur 1 et pour intervalle associé [0,4], mais les bornes de cet intervalle ne sont pas stockées dans ce sommet.
Enfin, le champ contenu ne sera utilisé qu'à partir de la question 10 et pourra être ignoré pour les deux questions suivantes.
Question 8. Écrire une méthode statique
static Arbre construireArbre(int[] x)
qui prend en argument un tableau déjà trié et sans doublon de k entiers x0 < x1 < x2 < … < xk−2 < xk−1 et retourne un arbre découpant l'intervalle [x0,xk−1] suivant les autres valeurs du tableau. On prendra bien garde à respecter les conditions définies dans le préambule et en particulier l'équilibrage.
|
Si un arbre représente l'intervalle
[xa, xb−1] alors sa racine porte comme valeur l'élément médian
xm avec m = (a+b)/2.
// On suppose que x contient au moins 2 entiers.
static Arbre construireArbre(int[] x) {
Arbre.XMIN=x[0] ;
Arbre.XMAX=x[x.length-1] ;
return construireArbre(x, 1, x.length-1) ;
}
// Construire l'arbre [x_a...x_{b-1}]
static Arbre construireArbre(int [] x, int a, int b) {
if (a == b) {
return new Arbre () ;
} else {
int m = (a+b)/2 ;
Arbre g = construireArbre(x, a, m) ;
Arbre d = construireArbre(x, m+1, b) ;
return new Arbre(x[m], g, d) ;
}
} |
Question 9. Écrire une méthode statique
static void imprimerIntervalle(int x, Arbre a)
qui affiche l'intervalle correspondant à la feuille de l'arbre contenant x.
Par exemple l'appel imprimerIntervalle(6, arbreDeLaFigure) doit afficher [5,7]. Si la valeur est une des valeurs de subdivision, on affichera l'intervalle réduit à un point; par exemple, l'appel imprimerIntervalle(5, arbreDeLaFigure) doit afficher [5,5]. On pourra utiliser une fonction auxiliaire récursive
void imprimerIntervalle(int x, Arbre a, int xGauche, int xDroit)
|
static void imprimerIntervalle(int x, Arbre a) {
imprimerIntervalle(x, a, Arbre.XMIN, Arbre.XMAX) ;
}
private static void imprimerIntervalle(int x, Arbre a, int low, int high) {
if (a.nature == FEUILLE) {
System.out.println("[" + low + ", " + high + "]") ;
} else {
if (x < a.valeur) {
imprimerIntervalle(x, a.filsGauche, low, a.valeur) ;
} else if (x > a.valeur) {
imprimerIntervalle(x, a.filsDroit, a.valeur, high) ;
} else {
System.out.println("[" + x + ", " + x + "]") ;
}
}
} |
Nous allons maintenant utiliser le champ contenu pour stocker
des listes de rectangles. Un rectangle [x,X]×[y,Y] sera
stocké dans chacun des sommets n tels que l'intervalle [x,X]
contienne l'intervalle associé à n mais ne contienne pas
l'intervalle associé au père de n.
On supposera dans toute la suite que l'arbre a été construit en utilisant les valeurs xmin et xmax des différents rectangles. Les valeurs x et X seront donc toujours des valeurs de subdivision de l'arbre (éventuellement égales à XMIN ou XMAX).
Question 10. Dans l'arbre de la figure, dans quels sommets doit-on stocker le rectangle [3,9]×[2,5]?
| Le rectangle [3, 9] × [2, 5] apparaîtra dans les listes des sommets correspondant aux intervalles [3, 4] (une feuille), [4,7] et [7,9] (une feuille). |
Question 11. Décrire le champ contenu de tous les sommets de l'arbre de la figure 1, si on y insère les rectangles de la figure 2.
Un petit dessin vaut un long discours.
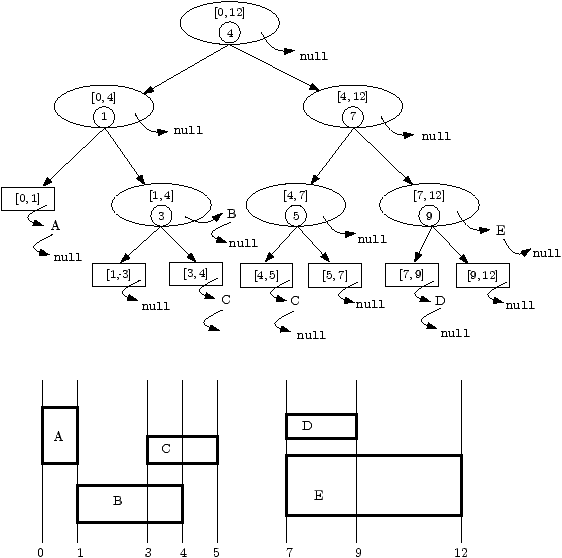 |
Question 12. Écrire une méthode statique
static void inserer(Arbre a, Rectangle r)
qui insère le rectangle r dans tous les sommets de l'arbre a où il doit être inséré.
|
static void inserer(Arbre a, Rectangle r) {
inserer(a, r, Arbre.XMIN, Arbre.XMAX) ;
}
static void inserer(Arbre a, Rectangle r, int low, int high) {
if (r.xmin <= low && high <= r.xmax) {
a.contenu = new ListeRectangle (r, a.contenu) ;
} else { // Noter que a.nature est nécessairement NOEUD (cf.
if (r.xmax <= a.valeur) {
inserer(a.filsGauche, r, low, a.valeur) ;
} else if (a.valeur <= r.xmin) {
inserer(a.filsDroit, r, a.valeur, high) ;
} else {
inserer(a.filsGauche, r, low, a.valeur) ;
inserer(a.filsDroit, r, a.valeur, high) ;
}
}
} Ce code est obtenu en limitant les appels aux sommets dont l'intervalle
intersecte [x, X] (intersection de mesure non-nulle).
On considère tout simplement les trois cas de positionnement possible
de la valeur et de l'intervalle.Un code équivalent et plus concis. static void inserer(Arbre a, Rectangle r, int low, int high) {
if (r.xmin <= low && high <= r.xmax) {
a.contenu = new ListeRectangle (r, a.contenu) ;
} else {
if (r.xmin < a.valeur) {
inserer(a.filsGauche, r, low, a.valeur) ;
}
if (a.valeur < r.xmax) {
inserer(a.filsDroit, r, a.valeur, high) ;
}
}
} |
Question 13. Si n est le nombre total de valeurs de subdivision dans l'arbre, dans combien de sommets un rectangle peut-il être inséré ? Le résultat le plus apprécié sera une majoration asymptotique en fonction de n.
|
Si les intervalles de deux sommets frères d'un même étage,
sont tous deux contenus dans [x,X] alors l'intervalle de leur père
(qui est la concaténation des deux intervalles)
est également contenu dans [x,X]. Par conséquent, un rectangle donné sera contenu dans au plus deux sommets par étage, soit en tout au plus 2(1+⌊ log2(p) ⌋) (Il y a 1+⌊ log2(p) ⌋) étages pour p sommets). La quantité n est le nombre de nœuds internes, on a p ≤ 2n. On peut donc considérer que la quantité demandée est en O(log(n)). |
Question 14. Écrire une méthode statique
static boolean estDansRectangles(int x, int y, Arbre a)
qui renvoie true si le point de coordonnées (x,y) est à l'intérieur d'au moins un des rectangles ayant été insérés dans l'arbre, et false sinon.
|
static boolean estDansRectangles(int x, int y, Arbre a) {
if (ListeRectangle.estDansRectangles(x, y, a.contenu)) { return true ; }
if (a.nature == FEUILLE) {
return false ;
} else {
if (x < a.valeur) {
return estDansRectangles(x, y, a.filsGauche) ;
} else if (x > a.valeur) {
return estDansRectangles(x, y, a.filsDroit) ;
} else {
return
estDansRectangles(x, y, a.filsGauche) ||
estDansRectangles(x, y, a.filsDroit) ;
}
}
} Le code ci-dessus est justifié ainsi :
|
La longueur d'un ensemble d'intervalles
s'obtient en redécomposant l'union de ces intervalles en union
d'intervalles disjoints dont on somme les longueurs.
On notera que cette longueur
n'est pas en général la somme des longueurs des intervalles
initiaux, en raison des éventuels recouvrements entre intervalles.
On insère dans l'arbre un ensemble fini de rectangles [xi, Xi] × [yi, Yi] (1 ≤ i ≤ m) en utilisant la méthode de la question 12. On ajoute alors dans la classe Arbre un champ longueur tel que, pour chaque sommet a associé à un intervalle W, le champ a.longueur contient la longueur de l'union de tous les intervalles [xi, Xi] ∩ W qui ont étés insérés dans le sous-arbre enraciné en a.
Par exemple, si on prend l'ensemble des rectangles représenté sur la figure 2, la longueur du sommet associé à [4,12] est 6, celle du sommet associé à [1,4] est 3, et celle du sommet associé à [1, 3] est 0.
Question 15. Récrire ou indiquer précisément les modifications à apporter à la méthode inserer de la question 12 afin de tenir ce nouveau champ longueur à jour.
Le plus simple est d'abord d'enrichir les objets de la classe
Arbre d'une méthode destinée à recalculer la longueur dans
tous les cas.
private void ajusterLongueur(int low, int high) {
if (contenu != null) {
longueur = high-low ;
} else {
if (nature == FEUILLE) {
longueur = 0 ;
} else {
longueur = filsGauche.longueur + filsDroit.longueur ;
}
}
} Il reste ensuite à appeler ajusterLongueur chaque fois que
celle-ci risque de changer.
static void inserer(Arbre a, Rectangle r, int low, int high) {
… // Code inchangé qui aboutit en séquence
a.ajusterLongueur(low, high) ;
} |
Question 16. Écrire une méthode statique
static ListeRectangle supprimer(ListeRectangle l, Rectangle r)
qui renvoie une liste contenant tous les éléments de l sauf r. Si le rectangle n'est pas présent on ne fait rien. On suppose que le rectangle figure au plus une fois dans la liste. Pour comparer des rectangles on utilisera l'opérateur ==.
|
Noter le codage récursif (mais destructif).
Un codage non-destructif fait tout aussi bien l'affaire.
static ListeRectangle supprimer(ListeRectangle l, Rectangle r) {
if (l == null) {
return null ;
} else {
if (l.contenu == r) {
return l.suivant ;
} else {
l.suivant = supprimer(l.suivant, r) ;
return l ;
}
}
} |
Question 17. Écrire une méthode statique
static void supprimer(Arbre a, Rectangle r)
qui supprime le rectangle r de tous les sommets où il figure dans l'arbre a, en n'oubliant pas de maintenir le champ longueur.
Ce code a la même structure que dans le cas d'inserer.
Ce qui est logique, car il s'agit ici d'identifier les sommets susceptibles de contenir le rectangle.
En fait, dans l'application envisagée (cf. la troisième
partie) on identifie exactement les sommets contenant le rectangle à
supprimer.
static void supprimer(Arbre a, Rectangle r) {
supprimer(a, r, Arbre.XMIN, Arbre.XMAX) ;
}
static void supprimer(Arbre a, Rectangle r, int low, int high) {
if (r.xmin <= low && high <= r.xmax) {
a.contenu = ListeRectangle.supprimer(a.contenu, r) ;
} else {
if (r.xmax < a.valeur) {
supprimer(a.filsGauche, r, low, a.valeur) ;
}
if (a.valeur < r.xmin) {
supprimer(a.filsDroit, r, a.valeur, high) ;
}
}
a.ajusterLongueur(low, high) ; // Noter l'ajustement de la longueur
} |
Cette dernière partie justifie les structures de données décrites dans les deux parties précédentes. Ces structures vont être cruciales pour calculer efficacement l'aire d'une union de rectangles.
L'algorithme consiste à balayer le plan par une droite horizontale, du bas vers le haut en maintenant dans un arbre de segments le sous-ensemble des rectangles coupés par la droite de balayage.
Lorsque la droite de balayage passe par le haut ou le bas d'un rectangle (événement), l'ensemble des segments coupés doit être mis à jour. Entre deux événements, la longueur de l'intersection permet de calculer facilement l'aire balayée.
Les événements pourront par exemple être définis ainsi :
class Evenement{
final static int HAUT = 0, BAS = 1;
int nature; //HAUT ou BAS
int ordonnee;
Rectangle contenu;
}
On suppose données deux méthodes de tri : l'une trie un tableau d'Evenement selon le champ ordonnee
static void trier(Evenement[] tableau)
et l'autre renvoie une copie triée et sans doublon de son argument
static int [] trier(int[] tableau)
Question 18. Écrire une méthode
static int aire(ListeRectangle l)
qui calcule l'aire de l'union des rectangles contenu dans la liste l en utilisant l'algorithme suggéré plus haut. On observera qu'en raison des recouvrements, cette aire n'est pas en général la somme de l'aire des rectangles.
|
Un code possible.
static int aire(ListeRectangle l) {
int r = 0 ;
// Construction de l'arbre (ie les abscisses)
int [] xs = ListeRectangle.abcisses(l) ;
xs = trier(xs) ;
Arbre a = construireArbre(xs) ;
// Construction du tableau d'evts (ie les ordonne'es)
Evenement [] ys = new Evenement [2*ListeRectangle.taille(l)] ;
int i = 0 ;
for (ListeRectangle p = l ; p != null ; p = p.suivant) {
ys[i++] = new Evenement (Evenement.BAS, p.contenu) ;
ys[i++] = new Evenement (Evenement.HAUT, p.contenu) ;
}
Evenement.trier(ys) ;
// Algo proprement dit
int yPrev = ys[0].ordonnee ;
inserer(a, ys[0].contenu) ;
for (i = 1 ; i < ys.length ; i++) {
r += (ys[i].ordonnee -yPrev) * a.longueur ;
yPrev = ys[i].ordonnee ;
if (ys[i].nature == Evenement.BAS) {
inserer(a, ys[i].contenu) ;
} else {
supprimer(a, ys[i].contenu) ;
}
}
return r ;
} On notera qu'en toute rigueur, la méthode trier(int [] t)
utilisée pour trier le abscisses (tableau xs) doit également
enlever les éventuels doublons. Cette méthode renvoie donc un nouveau
tableau.
|
Question 19. Estimer la complexité en temps et en mémoire de cet algorithme en fonction du nombre n de rectangles ? Cette complexité pourrait-elle être améliorée ?
|
Le coût dominant en espace est celui des listes de rectangles de l'arbre.
Chacun des n rectangles peut être stocké jusqu'à O(log(n)) fois.
L'espace consommé est donc O(n log(n)). Pour le temps, c'est la boucle de traitement des évènements qui domine, on pratique n insertions et n suppressions. Avec notre implémentation (listes de rectangles) ce sont les suppressions qui dominent avec, malheureusement un coût unitaire en O(n) à faire au plus O(log(n)) fois (car un rectangle donné se retrouve dans O(log(n)) listes). Soit O(n2 log(n)). Mais en fait, les listes de rectangles sont inutiles, on peut les
remplacer par un compteur correspondant à la longueur des listes,
l'insertion étant alors remplacée par un incrément et la suppression
par un décrément. Les coûts en mémoire et en temps deviennent alors
de l'ordre de O(n) et O(n log(n)) respectivement.
Il faut ici en toute rigueur remarquer que, pour un rectangle donné,
le nombre de sommets visités par |
This document was translated from LATEX by HEVEA.