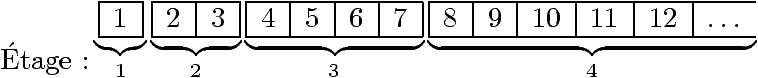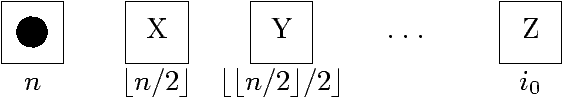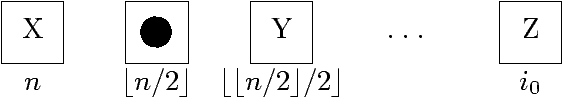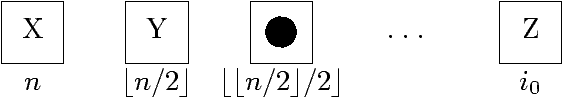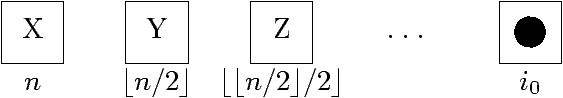Slide: 1
Égalité évoluée
Souvenez vous : premier arrivé premier servi (la file).
-
Dans les bus, ceux qui montent les premiers
sont les premiers à s'asseoir (parfois les seuls).
- Mais on tempère. Sont prioritaires (dans l'ordre) :
-
les mutilés de guerre,
- les invalides civils,
- les femmes enceintes,
- les femmes accompagnés d'enfants de moins de quatre ans.
- Plus informatique. L'ordonanceur (scheduler) traditionnel d'Unix
gère quelques niveaux de priorité.
Slide: 2
La file de priorité, quelques niveaux
Imaginons que la Poste organise ses files d'attente en suivant la
politique RATP.
-
Il faut gérer cinq files d'attente.
- Chaque utilisateur prend la file qui lui correspond.
- Chaque guichetier, quand il est libre, appelle le premier
usager de la file non-vide de plus haute priorité.
class Usager {
String nom ;
int prio ; // Dans [0..4]
}
Slide: 3
La Poste, comportement de l'usager
class Poste {
final static int NPRIO=5 ;
Fifo [] files ;
Poste () { files = new Fifo [NPRIO] ; }
void add(Usager u) { files[u.prio].add(u) ; }
}
L'usager u est enregistré par poste.add(u).
Et un usager s'enregistre par poste.add(this).
Slide: 4
La Poste, comportement du guichetier
Usager get() {
for (int i = 0 ; i < NPRIO ; i++) {
Fifo f = files[i] ;
if (!f.isEmpty()) { return f.get() ; }
}
throw new Error ("La poste est vide") ;
}
Le guichetier appelle poste.get() pour connaître l'usager
suivant selon le schéma de priorité.
Slide: 5
Autres exemples de priorités
-
Plus absurde, les radars automatiques :
-
Les radars alimentent un ordinateur central.
- Les infractions doivent être traitées par ordre de gravité
(dépassement de la limite de vitesse).
- L'exemple du TP (de l'anné dernière).
Gestion d'une file d'évènements.
-
Chaque évènement a un effet (dessin à l'écran et demande de
dessins dans le futur) et une date.
- Les dessins doivent être effectués par dates croissantes.
Dans ces exemples les priorités (dépassement de la limitation de
vitesse et date dans le futur) sont arbitraires.
Slide: 6
Priorités arbitraires
Nous sommes en fait confrontés au problème connu des associations :
à une priorité nous associons une file.
Allons au plus simple : listes d'associations, ordonnées
selon les clés (plus prioritaire d'abord).
class Alist { // Liste d'associations : priorité → file
int key ;
Fifo val ;
Alist next ;
…
}
Codage objet par encapsulage.
class FilePrio {
private Alist me ; // Liste d'associations
FilePrio () { me = null ; }
…
Slide: 7
Méthode add
void add (Object o, int prio) {
me = doAdd(o, prio, me) ; // NB me est this.me
}
private static Alist doAdd(Object o, int prio, Alist p) {
if (p == null || p.key < prio) {
Fifo f = new Fifo () ; f.add(o) ;
return new Alist(prio, f, p) ;
} else if (p.key == prio) {
p.val.add(o) ;
return p ;
} else { // Codage destructif, ici sûr
p.next = doAdd(o, prio, p.next) ;
return p ;
}
}
Slide: 8
Méthode get
Object get() {
if (me == null) { throw new Error("File vide") ; }
Object r = me.val.get() ;
if (me.val.isEmpty()) { me = me.next ; }
return r ;
}
Équivalents du coût, pour n grand,
| |
add |
get |
| Liste ordonnée |
n |
1 |
|
Liste quelconque |
n |
n |
|
Arbre équilibré |
log(n) |
log(n) |
Slide: 9
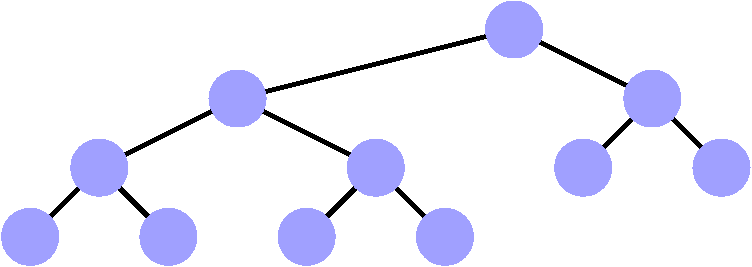
Les arbres (binaires) quasi-complets
-
Tous les étages sont remplis,
- Sauf, éventuellement, le dernier qui est
« tassé » vers la gauche.
Slide: 10
Exemples et contre-exemples
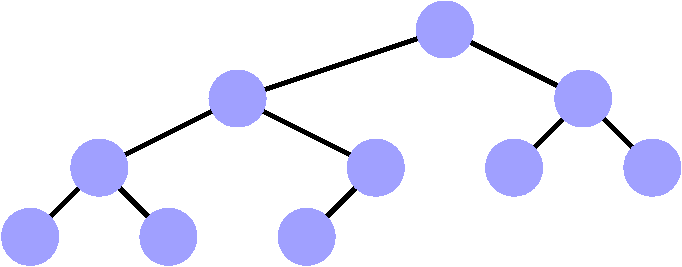 Oui
Oui
Noter : un des sommets de l'avant-dernier étage n'a
qu'un fils.
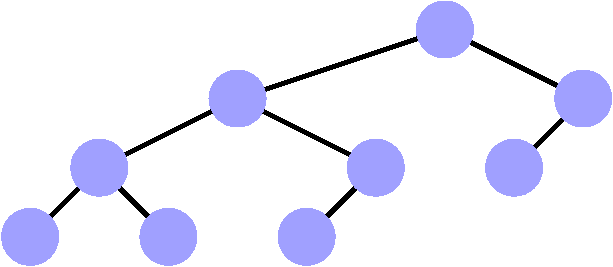 Non
Non, le troisième étage est incomplet.
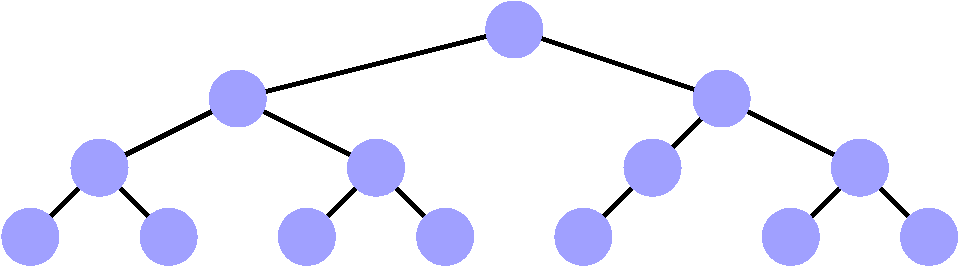 Non
Non, le dernier étage n'est pas « tassé ».
Slide: 11
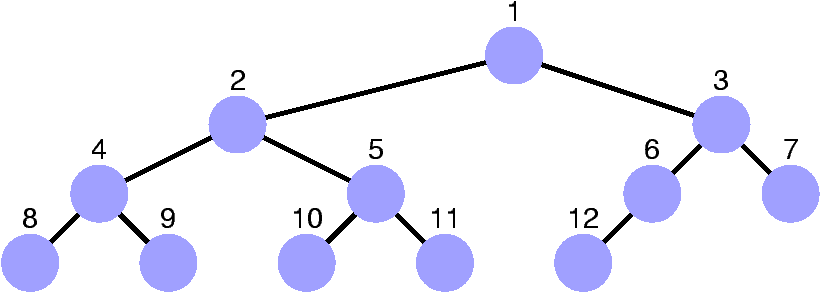
Arbres quasi-complets et tableaux
-
Numérotons les sommets selon un ordre « en largeur d'abord ».
- Et rangeons les sommets dans un tableau.
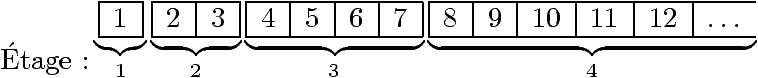
Slide: 12
Arbres quasi-complets et tableaux
En fait les arbres quasi-complets sont exactement les arbres
représentables ainsi dans un tableau :
-
On choisit de ranger la racine de l'arbre dans la case
d'indice 1.
- Indice des fils du sommet d'indice i ?
-
Fils gauche : 2 × i.
- Fils droit : 2 × i + 1.
- Parent du sommet d'indice i (i > 1) ?
⌊i/2⌋.
- La case d'indice i est un sommet de l'arbre à n sommets ? 1 ≤ i ≤ n.
Slide: 13
Bout de preuve
On numérote les sommets d'un arbre quasi-complet selon un parcours en
largeur d'abord :
Reste à montrer qu'il
y a i−1 sommets entre un sommet d'indice i et son fils gauche
(si il existe).
Et en effet, il y a :
-
d'abord 2d−1 − k sommets de l'étage d (les « successeurs »),
- puis 2 × (k−1) sommets de l'étage d+1
(les fils des prédécesseurs de l'étage d).
Soit en tout i−1 sommets.
Slide: 14
Bout de philosophie
-
Quelle est la hauteur d'un arbre quasi-complet à n sommets ?
⌊log2(n)⌋
- Avantage de la représentation en tableau.
-
Efficacité, économie de mémoire (avantage faible).
- Simplicité (notamment pour trouver le père d'un sommet).
- Avantage pédagogique : un arbre n'est pas nécessairement réalisé
en machine avec des objets, des flèches, des pointeurs, etc
(ici le « pointeur » est remplacé par un « indice »).
Slide: 15
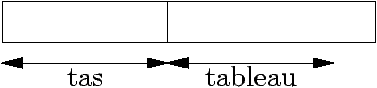
Le heap (tas)
Un tas est un arbre quasi-complet et :
-
Les sommets portent des clés ordonnées.
- La clé de tout sommet est supérieure ou égale à celles de ses
fils.
C'est un tas-max, il y aussi évidemment des tas-min.
Slide: 16
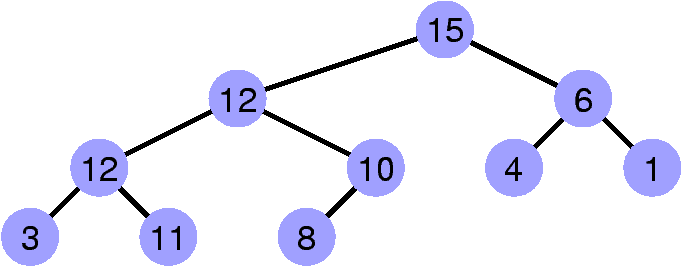
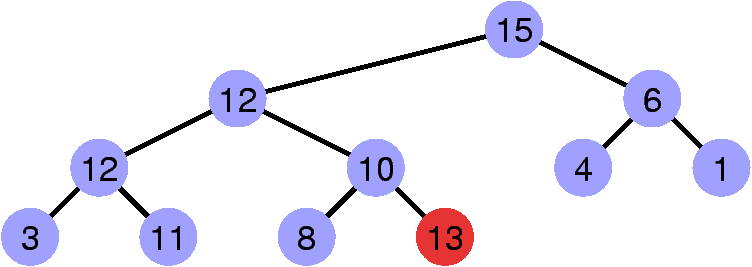
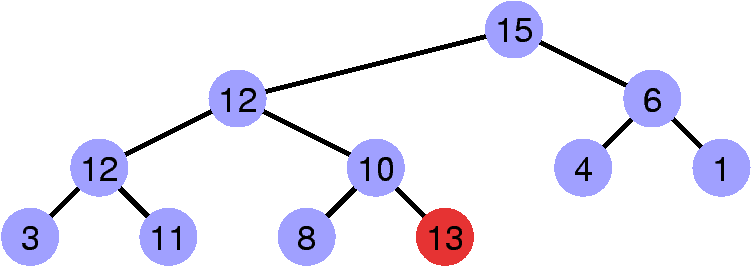
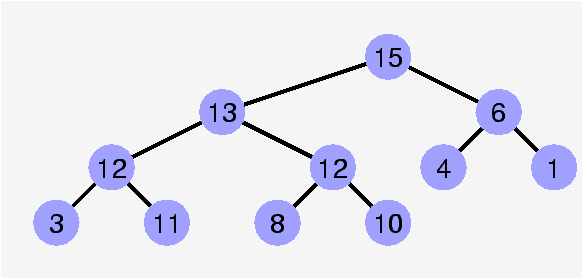
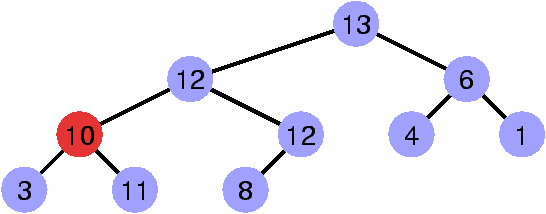
Contre-exemple
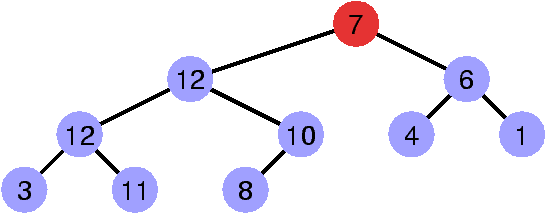
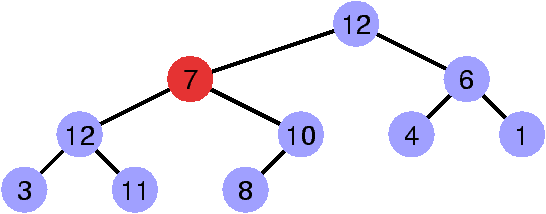
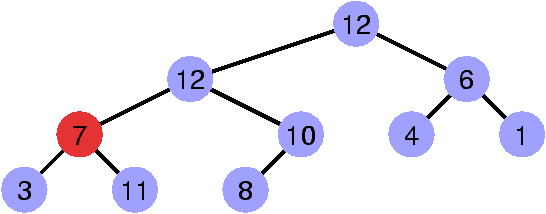
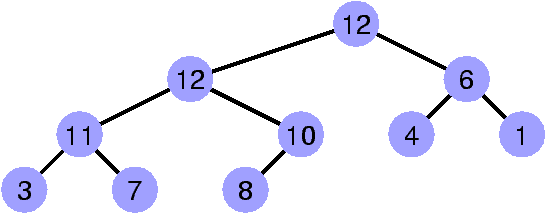
La propriété de heap est invalidée par le sommet de clé 13.
Slide: 17
Classe Heap
Les paires priorité × n'importe quoi.
class Pair {
int prio, Object val ;
… }
Les tas.
class Heap {
private Pair [] t ; // Tableau des sommets
private int n ; // Nombre de sommets
private final static int NMAX=128 ; // Par exemple
Heap() {
t = new Pair [NMAX+1] ;
n = 0 ;
}
…
}
Slide: 18
Slide: 19
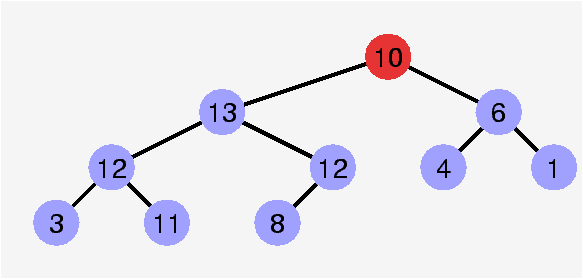
Invalidation de la propriété de heap
La position d'indice n+1 dans le tableau est la feuille « suivante ».
(Ajout d'un objet de priorité 13.)
Slide: 20
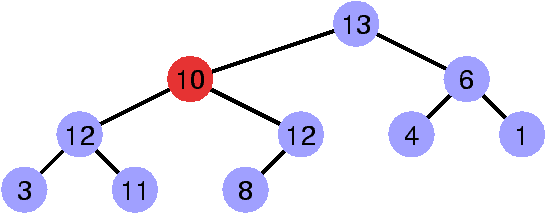
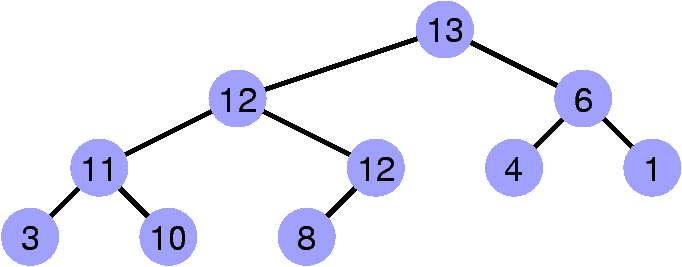
Restaurer la propriété de heap
Faire « remonter » le sommet invalidant.
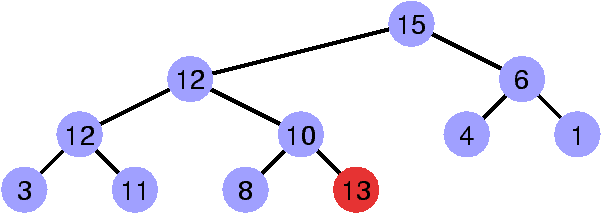
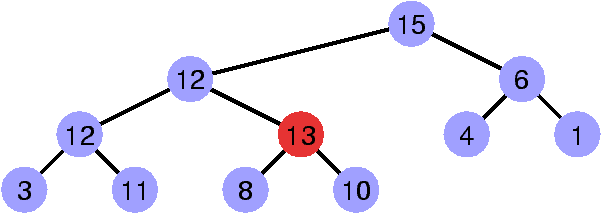
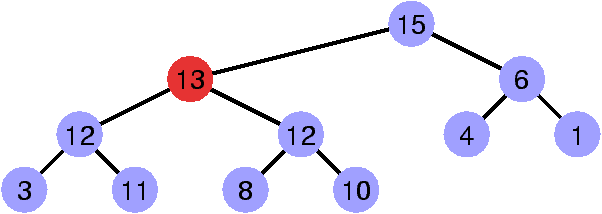
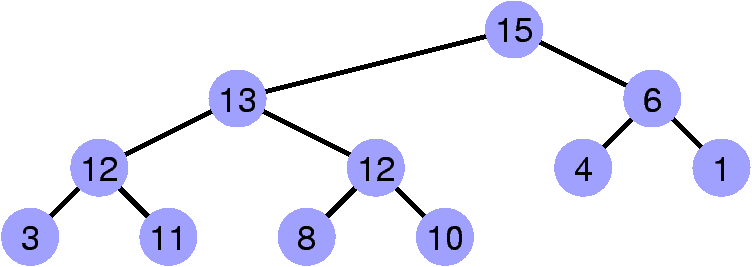
Slide: 21
Faire « remonter » un sommet
void add(int prio, Object o) {
n++ ;
int i = n ;
// Tant que i dans l'arbre et heap invalidé,
while (i > 1 && t[i/2].prio < prio) { // NB: division euclidienne
t[i] = t[i/2] ; // Libérer la case i/2
i = i/2 ;
}
t[i] = new Pair (prio, o) ;
}
Noter
Plutôt que d'échanger les cases, on fait remonter un trou.
Slide: 22
Slide: 23
Restaurer le heap II
Faire « descendre » le sommet invalidant.
Slide: 24
Descendre le sommet invalidant
Rappel : v est le sommet à « descendre ».
int i = 1 ; // À partir de la racine.
while (2*i <= n) { // Tant qu'il y a un fils
int j = 2*i ; // j Fils gauche
if (j+1 <= n && t[j+1].prio > t[j].prio){
j = j+1 ;
} // j fils de priorité maxi
if (v.prio >= t[j].prio) break ; // On a trouvé
t[i] = t[j] ; // Remonter t[j] en t[i] (i père de j)
i = j ;
}
t[i] = v ; // Ranger v à sa place
Noter Plutôt que d'échanger des cases, on fait descendre un
trou.
Slide: 25
Conclusion
-
Bonne complexité : log(n).
- Simplicité.
Deux problèmes pratiques
-
Les priorités égales.
- Notre heap a au plus
NMAX sommets.
Slide: 26
Les priorités égales
Et si il y a deux objets de même priorités ?
Pour le moment, aucune garantie.
-
Pour maintenir « premier entré/premier sorti à priorité égale »,
les priorités peuvent tenir compte du temps (logique).
- Une priorité est maintenant une paire, priorité × instant
d'entrée dans la file.
- Et on compare :
| (p1, t1) > (p2, t2)
⇔
|
⎧
⎨
⎩ |
| p1 > p2 |
| ou bien |
| p1 = p2 et t1 < t2 |
|
Slide: 27
Nouvelles priorités, réalisation
Les priorités deviennent des objets :
class Prio {
private static int time ; // Compteur des instants
private int prio ; // Priorité d'origine
private int t ; // Instant d'entrée
Prio (int prio) {
this.prio = prio ;
t = time ; // Pour this.t = Prio.time
time++ ; // N.B. time est une variable statique
}
…
Slide: 28
Comparaison des priorités
Par une méthode dynamique des objets de la classe Prio.
int compareTo(Prio o) {
if (this.prio > o.prio) {
return 1 ;
} else if (this.prio < o.prio) {
return -1 ;
} else { // this.prio == o.prio
if (this.t > o.t) {
return -1 ;
} else if (o.t < this.t) {
return 1 ;
} else {
return 0 ; // Ne devrait pas arriver
}
}
}
Slide: 29
Usage des nouvelles priorités
void add(int prio, Object o) {
Prio p = new Prio (prio) ; // créer priorité/avancer le temps
n++ ;
int i = n ;
// Comparaison par appel de compareTo
while (i > 1 && t[i/2].prio.compareTo(p) < 0) {
t[i] = t[i/2] ;
i = i/2 ;
}
t[i] = new Pair (p, o) ;
}
Remarquer Si l'entier prio ci-dessus est constant, on retrouve une
file ordinaire.
Slide: 30
Surmonter la taille fixée
C'est un grand classique (cf. piles et files).
private void realloc() {
Pair [] newT = new Pair [2*t.length] ;
for (int i = 1 ; i <= n ; i++) { newT[i] = t[i] ; }
t = newT ;
}
void add(int prio, Object o) {
if (n+1 >= t.length) { realloc() ; }
…
}
Noter Ajoutons n objets dans la file.
Le coût amorti (affecté à chaque opération add)
de l'allocation est constant.
-
On aura alloué successivement des tableaux de tailles
T0 (initial), T1 = 2 T0, ..., Tk, soit en tout moins de
2Tk cases.
- Or, Tk est de l'ordre de n (Tk/2 ≤ n ≤ Tk).
Slide: 31
Le tas-outil
Les tas sont un outil efficace pour extraire des maxima (minima),
à la volée.
-
Ajouter un élément à n : log(n).
- Extraire le maximum parmi n : log(n).
- Efficacité brute raisonnable (quelques opérations sur entiers et
tableaux).
Il sont souvent une brique d'algorithmes plus complexes
(parcours de graphes, recherche de solutions optimales diverses).
Par exemple : on trie facilement n éléments avec un tas :-
Ajouter les éléments : nlog(n).
- Extraire les maxima : nlog(n).
Slide: 32
heapsort naïf
static void sort(int [] t) {
Heap h = new Heap (n) ; // taille du heap donnée en argument
for (int k = 0 ; k < t.length ; k++) {
h.add(t[k]) ;
}
for (int k = t.length-1 ; k >= 0 ; k--) {
t[k] = h.get() ; // tas-max
}
}
L'idée de Robert W. Floyd, remonte à 1962.
On peut faire mieux (consommer moins de mémoire)
en cassant l'abstraction, afin d'utiliser t
comme tableau du tas !
Slide: 33
Méthode add
// t[0..n-1] est un tas
private static void add(int [] t, int n, int x) {
n++ ;
/* Attention les « vrais » indices commencent à zéro */
int i = n ; // i faux indice
while (i > 1 && t[i/2-1] < x) {
t[i-1] = t[i/2-1] ; // Libérer la case i/2
i = i/2 ;
}
t[i-1] = x ;
}
Méthode get
private static int get(int [] t, int n) {
⋮
}
Slide: 34
heapsort, en place
static void sort(int [] t) {
int n = t.length ;
for (int k = 0 ; k < n ; k++) {
add(t, k, t[k]) ;
}
for (int k = n-1 ; k >= 0 ; k--) {
t[k] = get(t, k+1) ; // tas-max
}
}
Dû à J. W. J. Williams (1964).
Mais...
On code souvent une autre version de heapsort en place.
Slide: 35
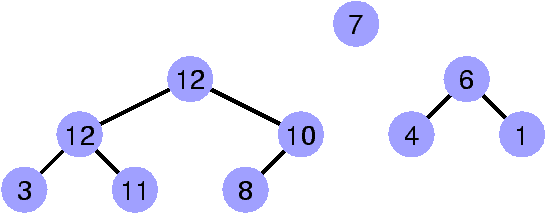
Construire le tas à partir des feuilles
Donnons nous deux tas, et un entier, et construisons un tas
qui regroupe tout le monde.
On procède donc à une descente, exactement comme pour get.
Slide: 36
Descente
Descendre la racine du tas de racine k, avec n limite des feuilles.
static void downheap(int [] t, int k, int n) {
int v = t[k-1] ; // valeur à « descendre »
int i = k ; // À partir de la racine, i « faux » indice
while (2*i <= n) { // Tant qu'il y a un fils
int j = 2*i ; // j Fils gauche
if (j+1 <= n && t[j+1-1] > t[j-1]){
j = j+1 ;
} // j fils de priorité maxi
if (v >= t[j-1]) break ; // On a trouvé
t[i-1] = t[j-1] ; // Remonter t[j] en t[i] (i père de j)
i = j ;
}
t[i-1] = v ; // Ranger v à sa place
}
Slide: 37
Un troisième heapsort
static void sort(int [] t) {
int n = t.length ;
for (int k = n/2 ; k >= 1 ; k--) { //NB commencer à n/2
downheap(t, k, n) ;
}
for (int k = n ; k >= 1 ; k--) {
/* 'get' écrit avec 'downheap' */
int max = t[0] ;
t[0] = t[k-1] ;
t[k-1] = max ;
downheap(t, 1, k-1) ;
}
}
Dû à Robert W. Floyd, (1964 aussi, six mois après).
Slide: 38
Pourquoi encore un heapsort
La complexité asympotique de la construction du tas est meilleure.
Soit n = 2k−1 (par exemple !). On « fabrique »
-
1 tas de hauteur k,
- 2 tas de hauteur k−1,
⋮
- 2k−2 tas de hauteur 2,
- et, (si on peut dire) 2k−1 tas de hauteur 1,
Soit un coût dans le cas le pire de l'ordre de :
|
(h−1)2k−h
= 2k−2 + |
|
(2 fois)
+ ⋯ +
|
|
(k−1 fois)
|
Slide: 39
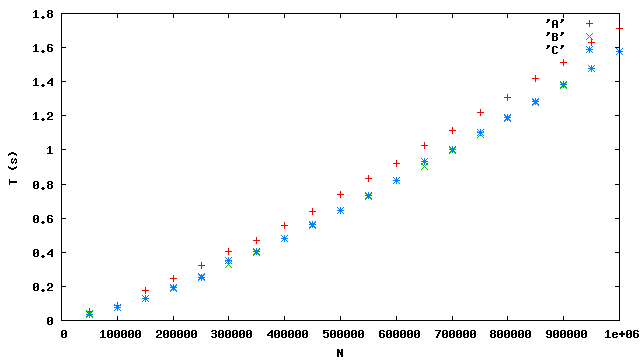
Tris d'un milion d'entiers
A est le heapsort naïf, B et C sont les
heapsort en place.
Conclusion : Tris un peu plus chers que linéaires.
B et C équivalents et un plus rapides que A
Slide: 40
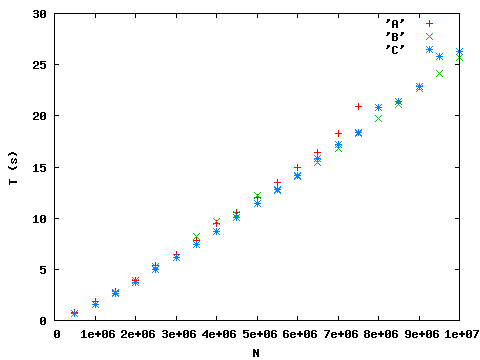
Tris de dix milions d'entiers
Conclusion :
Le tri naïf ne peut pas trier 8 milions et plus (par manque de mémoire),
les différences de temps sont peu significatives.
Slide: 41
Le mot de la fin sur les tris (de tableaux)
La librairie de java fournit une méthode de tri
impressionante.
La méthode
est dans la classe Arrays, du package
java.util.
static void sort(int [] t) { java.util.Arrays.sort(t) ; }
Selon la documentation, la méthode Arrays.sort
est écrite à partir de cet
article de Jon Bentley et M. Douglas McIlroy.
Ce document a été traduit de LATEX par HEVEA