Slide: 1
Une application concrète des arbres
-
Comment représenter un dictionnaire.
- Rechercher un mot.
- Construire le dictionnaire (à partir d'une liste de mots)
- Sauver/relire le dictionnaire.
- Fonctionnalités avancées :
-
Jouer aux mots-croisés.
- Proposer des corrections.
- Intersection de deux dictionnaires.
Diversion
Lire et écrire les fichiers.
Slide: 2
Du général au particulier
Prenons un peu d'avance sur le cours !
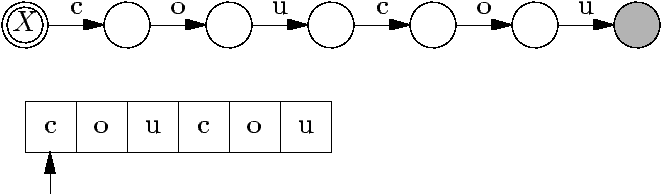
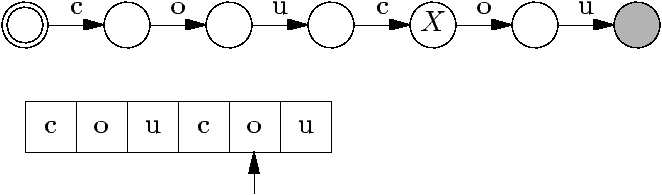
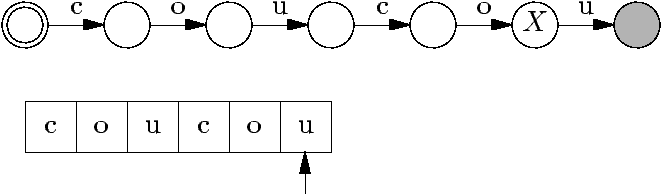
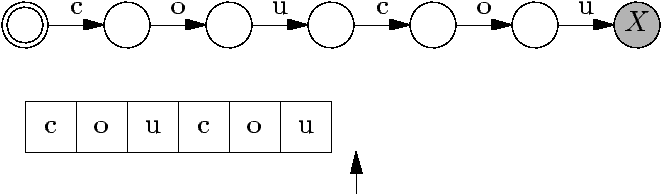
Les automates (finis) sont caractérisés par :
-
Un ensemble d'états, dont certains sont finaux et un est initial.
- Des transitions entre états, qui « mangent » des caractères en
entrée.
Voici par exemple l'automate qui reconnaît le mot coucou.
Slide: 3
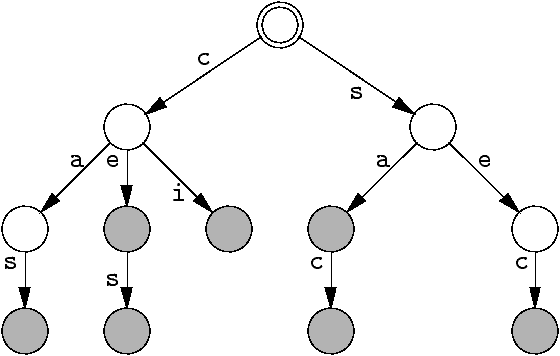
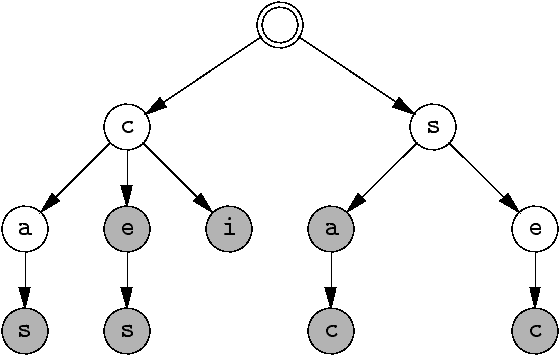
Plusieurs mots à la fois
Mots reconnus
cas,
ce, ces,
ci, sa, sac, sec.
Tous les chemins qui mènent à un état « final »
(sommet gris).
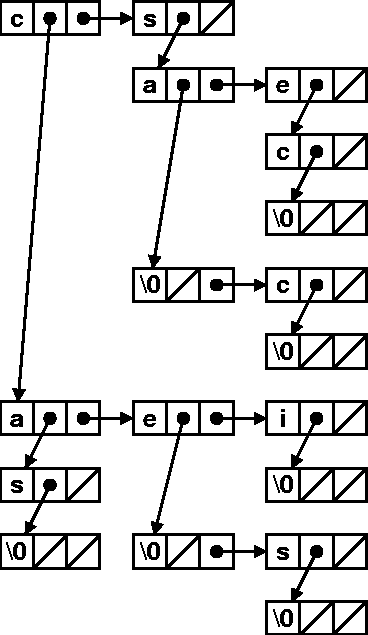
(Un tel arbre s'appelle parfois un trie).
Slide: 4
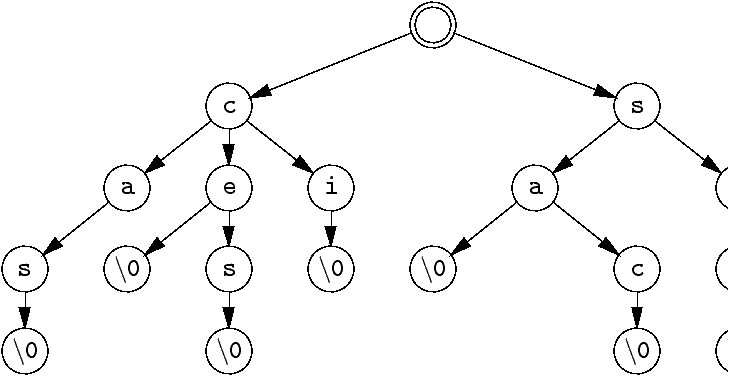
Réalisation des tries
Il y a plusieurs techniques, certaines très sophistiquées.
Ici, pour simplifier la programmation :
-
Au lieu de décorer les liens, on va, comme d'habitude décorer
les sommets de l'arbre (on pousse les étiquettes vers le bas).
- Au lieu de considérer des états finaux (sommets grisés),
on identifie les fins de mots par un marqueur
(le
char '\0').
- Et on transforme l'arbre n-aire en arbre binaire :
-
Tracer les liens entre frères (de gauche à droite).
- Supprimer les liens père/fils (sauf vers le premier fils).
- Si on y tient, dessiner un véritable arbre binaire
(mais à quoi bon !).
Slide: 5
Arbre en machine
class Tree {
char val ;
Tree down, next ;
Tree(char val) { this.val = val ; }
Tree(char val, Tree down, Tree next) {
this.val = val ;
this.down = down ; this.next = next ;
}
}
Cette structure ressemble fortement à un arbre binaire, mais
attention les deux fils (gauche et droit) jouent des rôles distincts :
-
Fils gauche : lettre suivante dans le mot.
- Fils droit : lettre suivante dans le dictionnaire.
Slide: 6
Une autre interprétation, parfois utile
Un dictionnaire est une liste de paires (char ×
dictionnaire), (c1, D1) ; ⋯ ; (cn, Dn) avec :
-
Les ci sont dans l'ordre : c1 < ⋯ < cn.
-
La paire (
'\\0', _) est le dictionnaire qui ne contient
que le mot vide.
- La paire (c, D) est l'ensemble des mots de la forme cw, où w
parcourt D.
- La liste (c1, D1) ; ⋯ ; (cn, Dn)
est l'union (disjointe)
des ensembles de mots (c1, D1),… (cn, Dn).
Dictionnaire vide
Il n'existe pas (i.e. notre construction va le garantir).
-
n > 1
- Aucun Di n'est vide.
Slide: 7
Test d'appartenance
Cette dernière interprétation est particulièrement utile pour
programmer les tests d'appartenance :
En toute logique, pour savoir si un mot w est dans un dictionnaire
(c1, D1) ; ⋯ ; (cn, Dn), on doit (surtout) :
-
Si w est le mot vide, alors chercher si c1 est la marque
de fin de mot ou pas.
- Sinon w = cw',
-
Trouver le ci tel que c = ci,
- Chercher w' dans Di.
Slide: 8
Chaînes terminées par une marque
La marque ne peut plus apparaître dans les chaînes.
Choisissons le charactère de code zéro (comme en C).
On veut extraire les caractères simplement.
class Tree {
…
final static char EOW = '\0'
static char getChar(String s, int i) {
return i < s.length() ? s.charAt(i) : EOW ;
}
}
Donc, au lieu de s.charAt(i) on fera
getChar(s, i).
Slide: 9
Test d'appartenance, première version
static boolean mem(String s, Tree t) {
char c = getChar(s,0) ;
if (c == EOW) {
return t.val == EOW ; // car liste triée (et non-vide)
} else {
for ( ; t != null ; t = t.next) {
if (c == t.val) {
return mem(s.substring(1), t.down) ;
// s.substring(1) renvoie s moins son premier caractère.
} else if (c < t.val) {
return false ; // car liste triée
}
}
return false ;
}
}
Slide: 10
Diversion
-
D'où vient
s.substring(1) ?
De la
doc !
- Pourquoi c'est moche ?
La recherche de
"coucou" entraîne la production de tous les
suffixes "oucou","ucou", ..., ""
(coût quadratique en la taille de la chaîne recherchée).
- C'est clairement un travail inutile.
- Représentons plutôt un suffixe par une chaîne et un entier i
indice du premier caractère du suffixe.
Slide: 11
Appartenance, seconde version
static boolean mem(String s, int i, Tree t) {
char c = getChar(s,i) ; // premier caractère du suffixe
if (c == EOW) {
return t.val == EOW ; // car liste triée
} else {
for ( ; t != null ; t = t.next) {
if (c == t.val)
return mem(s, i+1, t.down) ;
else if (c < t.val)
return false ; // car liste triée
}
return false ;
}
}
/* Conserver une interface simple */
static boolean mem(String s, Tree t) { return mem(s, 0, t) ; }
Slide: 12
Appartenance, code itératif
static boolean mem(String s, int i, Tree t) {
char c = getChar(s, i) ;
while (t != null) {
if (c < t.val) { return false } ; // aucun espoir
else if (c > t.val) { t = t.next ; } // à droite
else { // c == t.val, finir ou descendre
if (c == EOW) {
return true ;
} else {
i++ ; c = getChar(s, i) ;
t = t.down ;
}
}
}
return false ;
}
Slide: 13
Si on adopte le point de vue « arbre binaire »
Le code est peut-être moins simple à comprendre...static boolean mem(String s, int i, Tree t) {
if (t == null) { // Cas possible (fin de liste de paires)
return false ;
} else {
char c = getChar(s, i) ;
if (c < t.val) {
return false ;
} else if (c > t.val) {
// à droite, i inchangé
return mem(s, i, t.next) ;
} else { // c == t.val
// en bas, i incrémenté
return c == EOW || mem(s, i+1, t.down) ;
}
}
}
Slide: 14
Fabriquer le dictionnaire
Pour fabriquer le dictionnaire nous allons lire une liste de mots,
à raison d'un mot par ligne. Par exemple :
# cat /usr/share/dict/words
a
à
abaissa
abaissaient
abaissais
abaissait
abaissant
abaisse
abaissé
....
Slide: 15
Diversion, comment lire un fichier
En Java, pour lire un fichier...
Slide: 16
Entrées/Sorties bufferisées
Que veut dire « Buffered » dans BufferedReader ?
Il faut savoir qu'un accès au disque est beaucoup plus coûteux
qu'un accès en mémoire, et à peu près indépendant du nombre de
caractères transmis, dans une certaine limite.
Dans le BufferedReader il y a une zone de mémoire appelée
buffer (tampon). Quand on veut lire, disons, n caractères :
-
Le tampon contient plus de n caractères : les prendre dans le
tampon.
- Sinon, remplir le tampon à partir du fichier.
Avantage : efficacité.
Inconvénient : quand on écrit, on écrit en mémoire et pas
sur le disque. Il faut penser à vider le tampon (à la fin du traitement).
Slide: 17
Diversion, encore
Comment fabriquer les Reader etc.
-
Un
Reader à partir d'un nom de fichier.
Reader in = new FileReader (name) ;
// peut échouer (exception IOException)
- Avec l'entrée standard (qui n'est pas un
Reader).
Reader in = new InputStreamReader (System.in) ;
- On fabrique un
BufferedReader avec un...
Reader !
BufferedReader buffIn = new BufferedReader (in) ;
Bonus !
Il y a du sous-typage ici : les divers,
FileReader, InputStreamReader etc.
sont considérés comme de type Reader
(de même tout objet est un Object).
Slide: 18
Création du dictionnaire
Assez classiquement, on va ajouter tous les mots lus un
par un.
static Tree build(BufferedReader in) {
Tree r = null ;
String line ;
try {
while ((line = in.readLine()) != null) { // Idiome !
r = add(r, line) ;
}
} catch (IOException e) {
System.err.println(e.getMessage()) ;
System.exit(2) ;
}
return r ;
}
// Utiliser une méthode auxiliaire (cf. mem)
static Tree add(Tree t, String s) { return add(t, s, 0) ; }
Slide: 19
Principe de l'addition
On veut ajouter le mot w à un dictionnaire
D = (c1, D1) ; ⋯ ; (cn, Dn).
-
Si w est le mot vide, alors il suffit d'ajouter
(
'\0', _) à D.
- Sinon, w = cw' et on va procéder un peu comme pour un ajout
dans une liste triée,...
Code
static Tree add(Tree t, String s, int i) {// Attention! t peut être vide
char c = getChar(s, i) ;
if (c == EOW) {
if (t != null && t.val == EOW) { // Déjà là.
return t ;
} else { // Ajouter effectivement le mot vide.
return new Tree(EOW, null, t) ;
}
} else {
return addInList(t, c, s, i+1) ;
}} // ne renvoie jamais null
Slide: 20
Ajouter dans la liste de paires
Un principe, ajouter cw' dans D, démarche inductive.
-
Si la liste est vide, alors le nouveau dictionnaire est (c, {w'}).
- Sinon, D est (c1, D1) ; D', avec
-
Si c < c1, alors ajout devant (c, {w'}) ; D (comme ci-dessus).
- Si c = c1, alors il faut ajouter w' dans D1.
- Sinon (c > c1), il faut ajouter cw' dans D'.
Code
static Tree addInList(Tree t, char c, String s, int i) {
if (t == null || c < t.val) { // Ajouter devant
return new Tree(c, add(null, s, i), t) ;
} else if (c == t.val) { // Completer un sous-dictionnaire
return new Tree(c, add(t.down, s, i), t.next) ;
} else { // ajouter plus loin
return new Tree(t.val, t.down, addInList(t.next, c, s, i)) ;
}}
Slide: 21
Afficher le dictionnaire
Il « suffit » d'afficher tous les chemins qui mènent à '\0'.
Avec le point de vue « arbre binaire », code très concis.
static void print(PrintWriter out, Tree t, CharList path) {
if (t != null) {
char c = t.val ;
if (c == EOW) {
CharList.revPrintln(out, w) ;
} else {
print(out, t.down, new CharList(c, path)) ;
}
print(out, t.next, path) ;
}
}
Slide: 22
Comment afficher sur la sortie standard
-
Le
PrintWriter a les mêmes méthodes print et
println que les PrintStream, en (beaucoup) plus rapide
(dix fois sur ma machine !), car il est bufferisé.
- Deux exemples de
PrintStream : les increvables
System.out et System.err.
- Afficher un dictionnaire sur un
PrintStream.
static void print(PrintStream o, Tree t) {
PrintWriter out = new PrintWriter (o) ;
print(out, t, null) ;
out.flush() ; // C'est plus rapide, mais il faut vider
}
- Et enfin :
static void print(Tree t) { print(System.out, t) ; }
Slide: 23
Afficher le dictionnaire, avec une pile de
caractères
private static Stack path = new Stack () ; // NB: private
private static void doPrint(PrintWriter out, Tree t) {
if (t != null) {
char c = t.val ;
if (c == EOW) {
out.println(path) ; // affiche le contenu de la pile
} else {
path.push(c) ; doPrint(out, t.down) ; path.pop() ;
}
doPrint(out, t.next) ;
}
}
Avantage :
-
La mémoire peut être mieux gérée (pile réalisée par un
tableau).
- Pédagogique : lien entre pile et récursion.
Slide: 24
Mission de la méthode d'affichage
Quand on lui donne l'argument D et que la pile contient le mot p,
l'appel de print doit :
-
Afficher tous les mots de la forme pw,
où w parcourt D.
- Et rendre la pile dans l'état où elle a été trouvée.
Voyons l'appel récursif.
// La pile contient p
path.push(c) ;
// La pile contient p⋅c
doPrint(out, t.down) ;
// La pile contient p⋅c (induction)
path.pop() ;
// La pile contient p, CQFD.
Slide: 25
Initialisation de la pile
La pile est une variable globale.
private static Stack path = new Stack () ;
La pile étant créée vide, on peut écrire.
static print(PrintStream o, Tree t) { // Pas de private
PrintWriter out = new PrintWriter (o) ;
// La pile est vide.
doPrint(out, t) ;
// La pile est vide (rendue vide par doPrint).
out.flush() ;
}
Mais, on peut juger prudent d'écrire. Pourquoi ?
exception dans doPrint attrapée par l'appelant de
print
static print(PrintStream o, Tree t) {
path = new Stack () ;
… // Comme ci-desuss
Slide: 26
Au fait, on aurait pu écrire...
En prenant le point de vue D = (c1, D1) ; ⋯ ; (cn, Dn).
private static void doPrint(PrintWriter out, Tree t) {
if (t.val == EOW) {
out.println(path) ;
t = t.next ;
}
for ( ; t != null ; t = t.next) {
path.push(t.val) ; doPrint(out, t.down) ; path.pop() ;
}
}
}
Une boucle dans une récursion n'a rien d'effrayant.
Une question simple pour finir
Que se passe-t-il si on compose build et print :-
On trie le fichier d'entrée (ordre dit lexicographique).
- Et on élimine les doublons.
Slide: 27
Sauvegarder/Relire le dictionnaire
On pourrait relire la liste de mots et construire l'arbre pour chaque
usage.
Mais on peut procéder plus directement
-
Sauvegarder : parcours préfixe simple.
- Relecture : très simplifiée.
En outre le dictionnaire sera (un peu) compressé.
# ls -l fr fr.z
-rw-r--r-- 1 maranget moscova 1639367 Oct 14 12:39 fr.z
-rw-r--r-- 1 maranget moscova 2830676 Oct 8 19:41 fr
Slide: 28
Sauvegarder
final static char NULL = '\001' ;
static void save(Writer out, Tree t) throws IOException {
if (t == null) {
out.write(NULL) ;
} else {
out.write(t.val) ;
save(out, t.down) ;
save(out, t.next) ;
}
}
Note Pour écrire dans un fichier caractère par caractère, on
utilisera un Writer et sa méthode write, fabriqué tout à
fait comme les Reader (Il y a des BufferedWriter,
FileWriter etc, cf.
la Doc).
Slide: 29
Relire
static Tree read(Reader in) throws IOException {
int c = in.read() ;
if (c < 0) {
System.err.println("Fichier tronqué") ;
System.exit(2) ;
}
char x = (char)c ;
if (x == NULL) {
return null ;
} else {
Tree down = read(in) ;
Tree next = read(in) ;
return new Tree (x, down, next) ;
}
}
Slide: 30
Première application : assistant de mots croisés
Quand on remplit une grille de mots croisés, on cherche les mots :
-
Dont on connaît la longueur.
- Dont on connaît certaines lettres.
- Dont on connaît une « définition ».
Nous sommes en mesure de traiter les deux premiers points.
Un motif est un mot dont on ignore certaines lettres (remplacées par
'?').
Par ex :
-
Un mot de sept lettres commençant par ab et se terminant
par z ?
- Motif : ab????z.
- Comment feriez vous pour afficher tous les mots du
dictionnaire « filtrés » par le motif ?
Slide: 31
Une méthode
Un exemple (dictionnaire français de ∼ 260000 mots) :
#java Tree -pat 'ab????z'
abattez
abjurez
ablatez
abondez
abonnez
abordez
aboutez
aboyiez
abrasez
abritez
abrogez
abrégez
abusiez
abîmiez
-
Engendrer toutes les chaînes filtrées par le motif (il y en a disons
26n?).
- Tester l'appartenance au dictionnaire (
mem).
On peut faire bien mieux : parcourir l'arbre
(cf. print) en se limitant aux mots filtrés.
Slide: 32
Assistant de mots croisés
static void match(String pat, Tree t) { match(pat, 0, t) ; }
private static void match(String pat, int i, Tree t) {
char c = getChar(pat, i) ;
if (c == EOW) {
if (t.val == EOW) { System.out.println(path) ; }
} else {
if (t.val == EOW) { t = t.next ; }
if (c == '?') { // Joker
for ( ; t != null ; t = t.next) {
path.push(t.val) ; match(pat, i+1, t.down) ; path.pop() ;
}
} else { // Lettre ordinaire
…
Slide: 33
Assistant de mots croisés, lettre ordinaire
…
} else { // Lettre ordinaire
for ( ; t != null ; t = t.next) {
if (c < t.val) {
return ;
} else if (c == t.val) {
path.push(t.val) ; match(pat, i+1, t.down) ; path.pop() ;
return ;
}
}
}
}
}
Le coût est quelque part entre celui de mem (pas de '?')
et de print (que des '?').
Slide: 34
Deuxième application : suggestion de corrections
Lorsque le mot demandé n'est pas dans le dictionnaire, les bons correcteurs
orthographiques proposent une liste de mots du dictionnaire
« approchant » le mot faux demandé.
Nous allons faire de même en nous limitant à tenter de corriger
une faute de frappe :
-
Une lettre en moins (raté une touche).
- Une lettre en trop (appuyé deux touches à la fois).
- Une lettre changée (le doigt a glissé).
Un exemple :
# java Tree -error anticonstitutionellement
anticonstitutionnellement
anticonstitutionnellement
Pourquoi deux fois ? Il y a deux endroits où insérer « n ».
Slide: 35
Corriger une faute de frappe
private static void error(String w, Tree t) { error(w, 0, t) ; }
private static void error(String w, int i, Tree t) {
char c = getChar(w, i) ;
if (c == EOW) { // Ajouter une lettre à la fin de w
if (t.val == EOW) { t = t.next ; }
for ( ; t != null ; t = t.next) {
path.push(t.val) ; print(w, i, t.down) ; path.pop() ;
}
} else { // c est une lettre ordinaire
…
Slide: 36
Corriger une faute de frappe, lettre ordinaire
… // c est une lettre ordinaire
// Supprimer c
print(w, i+1, t) ;
// Changer et ajouter
if (t.val == EOW) { t = t.next ; }
for ( ; t != null ; t = t.next) {
path.push(t.val) ;
if (c == t.val) {
error(w, i+1, t.down) ;// pas (encore!) d'erreur
} else {
print(w, i+1, t.down) ; // Changer
}
print(w, i, t.down) ; // Inserer t.val ici
path.pop() ;
}
}
}
Slide: 37
Intersection de deux dictionnaires
Comment procéder simplement à partir des listes de mots ?
-
Trier les deux listes de mots.
- Procéder à une espèce de fusion.
On peut d'ailleurs procéder avec très peu de mémoire.
En supposant deux fichiers de mots triés
selon l'ordre compareTo des String.
On peut produire ce type de fichiers triés par la composition de build
et de print.
En effet, l'ordre compareTo est l'ordre lexicographique
qui étend l'ordre sur les char ainsi.
-
Si w1 et w2 vides alors ils sont égaux.
- Si w1 vide (et pas w2) alors w1 plus petit (et cas symétrique).
- Sinon w1 = c1w'1 et w2 = c2w'2, alors
-
Si c1 et c2 distincts, alors w1 et w2 ordonnés
comme eux.
- Sinon, w1 et w2 ordonnés comme w'1 et w'2.
Slide: 38
Intersection de deux listes de mots
Les « listes » sont en des fichiers, structurés en lignes,
à raison d'un mot par ligne.
static void inter(BufferedReader in1, BufferedReader in2)
throws IOException {
String buff1 = in1.readLine(), buff2 = in2.readLine() ;
while (buff1 != null && buff2 != null) {
int c = buff1.compareTo(buff2) ;
if (c < 0) { buff1 = in1.readLine() ; }
else if (c > 0) { buff2 = in2.readLine() ; }
else { // c == 0, ie buff1 et buff2 égaux
System.out.println(buff1) ;
buff1 = in1.readLine() ;
buff2 = in1.readLine() ;
}
Slide: 39
Intersection de deux dictionnaires
Un code très intéressant (à mon avis) qui mélange listes et
arbres...
D'abord intersection de deux dictionnaires non-vides.
static Tree inter(Tree a, Tree b) {
if (a.val == EOW && b.val == EOW) {
return new Tree(EOW, null, interList(a.next, b.next)) ;
} else {
return interList(a, b) ;
}
}
Slide: 40
Intersection de deux dictionnaires
Puis intersection de deux listes de paires (c,D).
static Tree interList(Tree a, Tree b) {
if (a == null || b == null) {
return null ;
} else if (a.val < b.val) {
return interList(a.next, b) ;
} else if (b.val < a.val) {
return interList(a, b.next) ;
} else { // a.val == b.val
Tree d = inter(a.down, b.down) ;
if (d == null) {
return interList(a.next, b.next) ;
} else {
return new Tree(a.val, d, interList(a.next, b.next)) ;
}
}
}
Ce document a été traduit de LATEX par HEVEA