Planche 1
Informatique
Amphi 0
Jean-Jacques.Levy@inria.fr
http://jeanjacqueslevy.net
secrétariat de l'enseignement:
Catherine Bensoussan
cb@lix.polytechnique.fr
Aile 00, LIX
tel: 34 67
http://w3.edu.polytechnique.fr/informatique/
Planche 2
Plan
-
Calculabilité
- Complexité
- Algorithmes simples
- Programmation
- Vaste domaine scientifique
- Organisation des cours
- Contenu du Tronc Commun
Planche 3
Un système étiqueté -- Tag system
|
Un mot de départ |
|
w = abccba |
|
|
Un nombre |
|
n = 3 |
|
|
Des règles |
|
a |® bab |
|
b |® abba |
|
c |® ca |
|
|
a |
bccba |
| a |
bc |
cba |
bab |
|
|
cbabab |
|
|
cbabab |
|
|
cba |
bab ca |
|
|
|
|
babca |
|
|
|
|
babca |
|
|
|
bab |
ca abba |
|
|
|
|
caabba
|
|
|
|
c |
aabba |
| caa |
bba ca |
|
bbaca |
|
bbaca |
|
bba |
ca abba |
|
|
caabba (arrêt car déja vu) |
|
|
|
Planche 4
Un autre petit jeu
|
Le mot de départ |
|
w = cabcba |
|
|
Le nombre |
|
n = 3 |
|
|
Les règles |
|
a |® cac |
|
b |® bab |
|
c |® ca |
cabcba
cbaca
caca
aca
cac
ca
a
c
(arrêt car mot vide)
Planche 5
Un troisième jeu
|
Le mot de départ |
|
w = 100110 |
|
|
Le nombre |
|
n = 3 |
|
|
Les règles |
|
0 |® 00 |
|
1 |® 1101 |
|
|
100110 |
|
1101101 |
|
11011101 |
|
111011101 |
|
0111011101 |
|
101110100 |
|
1101001101 |
|
10011011101 |
|
110111011101 |
|
1110111011101 |
|
01110111011101 |
|
|
|
1011101110100 |
|
11011101001101 |
|
111010011011101 |
|
0100110111011101 |
|
011011101110100 |
|
01110111010000 |
|
1011101000000 |
|
11010000001101 |
|
100000011011101 |
|
0000110111011101 |
|
011011101110100 |
|
(arrêt car déja vu) |
Planche 6
Terminaison
-
le jeu 1 peut ne pas terminer
- le jeu 2 termine toujours
- la terminaison du jeu 3 est un problème ouvert
Question
Peut-on déterminer par programme la terminaison
d'un jeu donné par w, n et {a1 |® A1, a2 |® A2,
... ap |® Ap} (n³ 0, p³ 0) ??
Réponse [Post, 1925]
Non. La terminaison des systèmes étiquetés est indécidable.
Planche 7
Dominos de Wang
| Un ensemble |
|
Paver un carré |
|
| de p = 4 motifs |
|
de taille n = 6 |
| (carrés à bords colorés) |
|
|
 |
|
 |
 |
Deux motifs adjacents ssi leurs cotés communs de
même couleur.
Rotations et symétries sont interdites.
Planche 8
Dominos de Wang -- bis
Planche 9
Au dela du jaune et du rouge
Planche 10
Pavage d'un carré
-
Données: p motifs et un carré de taille n.
-
Algorithme: énumérer les pn2 pavages possibles et ne garder
que les pavages licites.
-
Complexité: O(pn2)
Dans l'exemple précédent
n=6, p=3
150094635296999121 » 1017 tests à effectuer
Soit 57 jours en comptant 500 × 106 opérations à la seconde.
Faire mieux?
Planche 11
NP complétude
Personne ne sait faire mieux.
Ce problème est représentatif d'une grande classe de
problèmes, dits NP complets.
Si on sait faire mieux pour ce problème, on saura le faire pour
toute la classe NP.
Conjecture: P ¹? NP [Cook, 1973]
Un des 10 problèmes ouverts les plus importants des mathématiques
(cf. Majeure 2 d'Informatique)
Planche 12
Pavage du plan
-
Données: p motifs
-
Problème: paver tout le plan
équivalent à
-
Données: p motifs
-
Problème: paver les carrés de taille n pour tout
n ³ 0
Réponse
Le pavage du plan par p motifs est indécidable
Planche 13
Pavages non périodiques
Conjecture de Wang (1973): tout pavage du plan est périodique.
Et grâce à cette périodicité, on sait décider du pavage du plan.
Indécidabilité Þ existence de pavages non périodiques.
Conclusion: en passant par des théorèmes d'informatique
théorique, on peut résoudre des problèmes de math.
(Itou pour la physique)
En 1975, les pavages non périodiques ont fleuri. Pavages
quasi périodiques de Penrose.
Planche 14
Exemple de pavage de Penrose

Planche 15
Théorie de la calculabilité
Comment montrer qu'un problème est indécidable?
Par contradiction: si le problème est décidable, un problème
indécidable connu deviendrait décidable.
Comment montrer l'indécidabilité de ces problèmes de base?
Par diagonalisation et reflexivité.
Exemple connexe: Soit S l'ensemble de tous les ensembles. Alors
S Î S. Mais pour l'ensemble X = {T | T ÏT}. Alors X Î X ssi X ÏX.
[Gödel, Church, Turing, Kleene, Post; 1920-1940]
[von Neumann; 1940]
Planche 16
Faits
Il existe des
-
problèmes indécidables
- problèmes décidables de complexité élevée
En pratique
-
problèmes ou sous-cas
de faible complexité algorithmique,
typiquement en O(na) avec a £ 3
- suffisant pour construire les cathédrales informatiques
des années 2000
La décidabilité est étudiée en Majeure 1.
La complexité des algorithmes en Tronc Commun et Majeure 2.
Planche 17
Exemples d'algorithmes ``simples''
-
tri
- recherche en table
- gestion d'une file de priorité
- analyse syntaxique
- évaluation des expressions arithmétiques
- marche du cavalier sur un échiquier (algorithme glouton)
- parcours en profondeur d'abord (connexité dans un graphe)
- recherche du plus court chemin dans un graphe
- etc.
Planche 18
Programmation
| |
algorithmes |
|
|
langage des mathématiques |
|
| |
programmes |
|
|
langages de programmation |
|
- exécution par une machine Þ précision supplémentaire
- complexité dans l'organisation des programmes et des données
Þ modularité
- catalogue de méthodes de programmation bien connues
qui s'apprennent
- choix important du langage de programmation
Planche 19
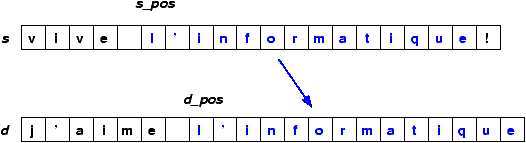
Un programme tout simple
static void copie (char[] s, int s_pos, char[] d, int d_pos,
int longueur) {
for (int i = 0; i < longueur; ++i)
d [d_pos + i] = s [s_pos + i];
}
Complexité O(n) si n est la longueur.
Ce programme est-il correct?
Planche 20
Attention aux alias
Bug si s et d sont deux alias (s = d)
Le programme correct:
static void copie (char[] s, int s_pos, char[] d, int d_pos,
int longueur) {
if ( s != d || d_pos <= s_pos)
for (int i = 0; i < longueur; ++i)
d [d_pos + i] = s [s_pos + i];
else
for (int i = longueur - 1; i >= 0; --i)
d [d_pos + i] = s [s_pos + i];
}
La recherche d'alias dans un programme est un problème important
(Ariane 5, Word 97, Windows 2000, etc).
Analyse statique de programmes.
Planche 21
Sémantique des opérateurs
static String paques (int y){ y = 11571
int g = (y % 19) + 1; g = 1
int c = y / 100 + 1; c = 116
int x = 3 * c / 4 - 12; x = 75
int z = (8 * c + 5) / 25 - 5; z = 32
int d = 5 * y / 4 - x - 10; d = 14378
int e = (11 * g + 20 + z - x) % 30; e = -12
if ( e == 25 && g > 11 || e == 24 )
++e;
int n = 44 - e; n = 56
if (n < 21)
n = n + 30;
int j = n + 7 - ((d + n) % 7); j = 63
if (j > 31)
return (j - 31) + " avril"; 32 avril
else
return j + " mars";
}
Que vaut le modulo d'un nombre négatif?
Planche 22
Domaine des valeurs
- Ariane 501: dépassement de capacité dans le système de guidage
par inertie en convertissant un flottant 64 bits en entier 16 bits
Þ exception processeur Þ traitement de
l'exception en basculant sur le processeur de secours Þ
arrêt puisque ce processeur exécutait le même programme qui avait lui
aussi fait la même exception.
- Coût: 109FF
- Leçon: ne pas penser qu'aux erreurs matérielles.
Le logiciel peut aussi être erronné.
Les principes des langages de programmation sont étudiés en Majeure 1.
L'analyse statique est enseignée en DEA.
Planche 23
Au dela
- certification des programmes
- logique mathématique et preuves mécaniques
- systèmes d'exploitation
- architecture des processeurs et ordinateurs
- compilation
- CAO de circuits
- technologie (semi-conducteurs, physique quantique)
- réseaux
- protocoles et sécurité
- bases de données distribuées (Web)
- traitement et synthèse d'images
- etc.
Planche 24
Quelques domaines d'application
- Transports/Espace
- Médecine
- Biologie
- Télécommunications
- Monétique
- Environnement/Météo
- Cinéma/Multimédia
- Productique/Robotique
- Documentation/Enseignement
- Jeux
- Impact sur l'économie (start-ups)
- etc.
Planche 25
Monétique
Cartes à puce programmable en Java (Javacard).
Intérêt:
-
charger de nouveaux services (banques multiples, carte
téléphone, carte médicale, programmes de fidélisation, etc)
- programmation des services dans un langage de haut niveau
Espace limité: 32 KO de ROM, 8 KO d'EEPROM (bytecode),
512 octets de RAM (pile).
Les programmes chargés sont-ils sûrs?
Þ Analyse statique ou preuves formelles.
(La France est bien placée.)
Planche 26
Télécommunications
-
puissance de calcul dans un téléphone mobile est de 40 MFlops
(opérations flottantes par seconde)
- 600 Gbits/sec passent sur un fil sans répéteur sur 10000km
Planche 27
Une technologie exponentielle
| |
gain |
période |
| densité des puces |
× 2 |
18 mois |
| vitesse processeur |
× 2 |
18 mois |
| capacité
mémoire |
× 4 |
3 ans |
| coût/octet
disques |
× 0.75 |
1 an |
En 2000,
-
Processeur à 750 MHz, 10M transistors, (» 1300 × Vax)
-
RAM 128 Mbits, 133 MHz
-
Disques 2.5" à 18GO, 3.5" à 20GO (1 kF)
-
Réseaux ATM à 640 M bits/sec
-
Internet avec 80 M machines
Planche 28
Vers un ordinateur mondial
Le World Wide Web est déjà une bibliothèque mondiale.
Ira-t-on vers un calculateur mondial?
L'exemple de la cryptographie:
-
F9 = 2 512 + 1 =
1340780792994259709957402499820584612747936582059239337772356144372176
4030073546976801874298166903427690031858186486050853753882811946569946
433649006084097 =
2424833 × 7455602825647884208337395736200454918783366342657
×
7416400626275308015247871419019374740599407810975190239058213161444157
59504705008092818711693940737 [Manasse, Lenstra] en 1990.
-
RSA-155 =
1094173864157052742180970732204035761200373294544920599091384213147634
9984288934784717997257891267332497625752899781833797076537244027146743
531593354333897 =
1026395928297411057720541965739916759007165678080380668033419335217907
11307779 × 106603488380168454820927220360012878679207958575989291
522270608237193062808643
(35 ans de machine de 400 MHz avec 300 machines en 7 mois)
[Lenstra, Odlysko, ...Morain] en 1999.
-
ECC2K-108. Soient P et Q deux points sur une courbe elliptique
munie d'une opération Ä formant un groupe de ~
2108 éléments. Trouver n tel que Pn = Q.
Réponse:
n = 47455661896223045299748316018941 mod
324518553658426701487448656461467 (500 ans de machine de 450 MHz avec
9500 machines de 40 pays en 5 mois) [Harley et al] en 2000.
- ...à l'écoute des extra terrestres (projet SETI)
Planche 29
L'informatique et l'X
-
Futurs ingénieurs doivent connaître l'informatique
-
Former de bons informaticiens (vs ENS, ETH, MIT)
-
Recherche en informatique en plein essor
-
Mathématiques Þ rigueur Þ atout
en informatique
(vrai en général)
-
Formation initiale très hétérogène des élèves
(dramatique)
-
L'environnement informatique de l'X est bon. Il faut s'en servir.
-
Format du cours demande un peu de travail personnel
(beaucoup moins que les 15h/semaine de cours analogues)
Planche 30
Enseignement de l'informatique à l'X
| Tronc Commun, obligatoire |
| 1ère année, 1er semestre; |
| Projet informatique, |
| 1ère année, 2ème semestre |
|
|
| Voie C, optionnelle |
| 1ère année, 2ème semestre |
|
| Majeure 1, optionnelle |
| 2ème année, 1er trimestre |
|
|
| Majeure 2, optionnelle |
| 2ème année, 2ème trimestre |
|
|
|
|
Planche 31
Contenus
Tronc Commun: algorithmes et programmation
Lévy (projet informatique Gonthier)
Voie C: optimisation combinatoire
Steyaert
Majeure 1: mathématiques et informatique
Steyaert
automates et calculabilité, architecture [Vuillemin],
algèbre Ú bases de donnée Ú lang. de programmation,
1 cours au choix (automates, vision, objets, ...)
Majeure 2: informatique
Cori et Toueg
systèmes et réseaux, complexité,
algorithmes distribués Ú compilation,
1 cours au choix (crypto, synthèse d'images, ...)
Planche 32
Organisation du Tronc Commun
-
2.5 travaux dirigés d'initiation
- 10 petites classes + 10 travaux dirigés
- contrôle hors-classement, 2h;
composition de classement, 4h,
Coefficient 10.
Théorique.
- projets de programmation,
~1000 lignes de Java (en binôme)
20 sujets différents de difficultés variées,
Coefficient 8.
Pratique, travail personnel.
Groupes de niveaux (Forts, Moyens, Débutants)
Planche 33
L'équipe enseignante du Tronc Commun
-
Ecole polytechnique: 1 professeur, 10 maîtres de conférences, 11 chefs
de travaux pratiques, 11 vacataires, 1 secrétaire.
-
Cours: 4 prof. univ., 5 DR, 1 CR, 1 ingénieur Mines
-
TD:
6 CR, 3 MdC, 1 ingénieur Mines, 10 thésards.
- les enseignants sur poste sont tous des chercheurs reconnus.
Centre informatique de l'X
-
Climat de confiance. Très
difficile à 460 (900) élèves.
- Impression (» 10-20 centimes la page). Ne pas faire des
impressions inutiles. Utiliser les photocopieuses.
Planche 34
Le contenu du Tronc Commun
| programmes |
itération |
récursion |
|
| structures |
tableaux |
arbres |
graphes |
| de données |
listes |
listes |
|
| |
files, piles |
|
|
| algorithmes |
tri |
| |
recherche en table |
| |
analyse syntaxique |
| |
exploration |
| projet |
modularité |
| informatique |
|
Langage de programmation
Java, [Gosling et Sun microsystems]
langage typé + garbage collector
Planche 35
Lisez nos pages Web!
Envoyez nous des e-mails.
Téléphonez nous. Venez nous voir.
Travaillez l'informatique.
On y trouve beaucoup de métiers intéressants.
This document was translated from LATEX by HEVEA.