Contrôle Classant d'Informatique
Promotion 1998
Sujet proposé par Robert Cori et François Morain
26 janvier 2000
Les téléphones mobiles sont partout. Avec eux sont arrivés des
problèmes algorithmiques rendus plus complexes en raison du
grand nombre de clients à
satisfaire en même temps. Le problème est consacré à quelques
questions inspirées par la gestion de réseaux de mobiles.
La partie I comporte surtout de la programmation. Les
parties II et III du problème sont indépendantes de la
partie I. La partie III reprend la problématique de la partie II.
Un réseau de téléphones mobiles est constitué de régions, chacune
pouvant gérer un grand nombre de mobiles. L'ordinateur central du
réseau a pour tâche de trouver la région contenant un mobile de
numéro donné, ce qui permet de mettre en communication le mobile
et l'appelant. On s'interessera dans la première partie à la
gestion des mobiles dans une région et dans les deuxièmes et
troisièmes parties aux communications entre les régions.
I. Gestion de la localisation
Une région est assimilée à une partie du plan euclidien.
Chaque région contient une balise fixe permettant d'émettre
et de recevoir des messages pour les mobiles présents
dans la région.
Un mobile est repéré par son numéro de téléphone (qu'on
suppose être un entier),
ainsi que par ses coordonnées (x, y) qui sont entières.
Il s'agit en fait de la position du mobile dans un quadrillage
relativement large.
À une région donnée est associée une liste des mobiles
qui s'y trouvent. Chaque cellule de la liste contient le numéro d'un
mobile, ses coordonnées et l'adresse de la cellule suivante. Ceci
est déclaré par une classe Java, à l'intérieur de laquelle sont
incluses les méthodes demandées dans les questions 1, 2, 3, 4.
class ListeM{
int xm, ym;
int num;
ListeM suiv;
ListeM(ListeM l, int x, int y, int n){
xm = x; ym = y; num = n; suiv = l;
}
}
La distance entre deux mobiles M1 de
cooordonnées (x1, y1) et M2 de coordonnées (x2, y2) sera
calculée par la formule d(M1, M2) = |x2-x1|+|y2-y1| (on
montre que c'est bien une distance) où |z|
désigne la valeur absolue. Dans la suite on note N le nombre de
mobiles présents dans la région.
Question 1.
a) Écrire une méthode :
static int distance(int x1, int y1, int x2, int y2)
qui calcule la quantité |x2-x1|+|y2-y1|. On rappelle que la
valeur absolue d'un entier s'obtient en Java au moyen de la
fonction Math.abs.
b) Écrire une méthode :
static ListeM estDansListe(ListeM lm, int num)
qui renvoie (sans copie) la fin de la liste lm commençant
par le mobile de numéro num si celui-ci figure dans la liste et
null sinon.
c) Écrire une méthode :
static int distanceM(ListeM lm, int num1, int num2)
qui calcule la distance de deux mobiles présents dans la région
et donnés par leurs numéros.
Question 2.
a)
Écrire une méthode :
static int plusPetiteDistance(ListeM lm, int x, int y)
qui renvoie la plus petite distance (au sens de la distance d) entre
un mobile de lm et le point (x, y).
b) Écrire une méthode :
static ListeM plusProches(ListeM lm, int x, int y)
qui renvoie la liste des mobiles les plus proches du point (x, y).
On suppose maintenant qu'une région est découpée en
sous-ensembles de taille plus petite. Chaque
sous-ensemble est représenté par la liste des mobiles qu'il
contient. Une région est donc représentée par un tableau de
taille RMAX dont chaque élément est une liste de
mobiles.
Il est déclaré et initialisé par
ListeM[] reg = new ListeM[RMAX];
On suppose donnée une fonction h qui à tout numéro de
téléphone associe le numéro du
sous-ensemble qui le contient. Ainsi deux mobiles de numéro n1 et
n2 sont dans le même sous-ensemble si et seulement si h(n1)=
h(n2). On supposera cette fonction réalisée par une méthode
donnée h, qui opère en temps constant :
static int h(int numero){ ... }
Question 3.
a) Écrire une méthode
static int distanceM2(ListeM[] reg, int num1, int num2)
calculant la distance entre deux mobiles donnés par leurs numéros
avec cette nouvelle structure de données.
b) Donner une méthode
static ListeM plusProches2(ListeM[] reg, int x, int y)
qui renvoie la liste des mobiles les plus proches d'un point donné.
c) Gagne-t-on en efficacité dans ces méthodes grâce à
cette nouvelle structure de données? On supposera que le nombre de
mobiles dans chaque sous-ensemble est petit par rapport au nombre
total de mobiles N.
Question 4.
Suite à un accroissement du nombre de mobiles dans une
région, on décide de couper celle-ci en deux, en installant une
nouvelle balise aux coordonnées (xb, yb). La nouvelle balise
prendra en charge les mobiles plus proches (au sens strict) d'elle que
de la balise initiale de coordonnées (xa, ya). Donner une
méthode
static void divise(ListeM[] rega, ListeM[] regb, ListeM[] reg,
int xa, int ya, int xb, int yb)
de complexité linéaire en N permettant d'accomplir cette tâche, dans le
cas où on utilise une gestion par sous-ensembles comme dans la question
précédente. Cette méthode remplit les régions rega et
regb à partir de reg.
II. Attribution de fréquences
On considère dans cette partie les communications entre les balises
figurant au centre de chaque région.
Celles-ci émettent chacune sur une certaine fréquence.
Deux balises voisines ne peuvent
émettre sur la même fréquence en raison des interférences.
On s'intéresse à des algorithmes d'attribution de fréquences
satisfaisant cette contrainte.
On modélise un réseau par un graphe G=(B, V) où B est
un ensemble de balises et V l'ensemble des arêtes. Deux balises
sont liées par une arête si et seulement si elles peuvent
émettre l'une vers l'autre. Le graphe est symétrique (non
orienté) : si la balise i émet vers j alors j peut
émettre vers i.
On appelle étiquetage du graphe G une application j de
B dans N telle que deux balises voisines ont une image
différente par j .
On note N(j ) le nombre de fréquences qu'elle utilise,
c'est-à-dire le cardinal de l'image de j dans
N. Dans la pratique, il est important de chercher à
minimiser ce nombre. Le nombre minimal de fréquences nécessaires
pour étiqueter un graphe sera noté n(G).
À titre d'exemple, le graphe suivant est étiqueté :
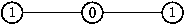
On a mis pour chaque balise la fréquence associée.
Question 5.
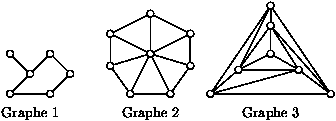
Déterminer le nombre n(G) pour les graphes
suivants en exhibant un étiquetage convenable.
Le degré d'une balise bÎ B est le nombre de balises
voisines de b dans G ; on le note deg(b). Le degré du
graphe G est le maximum des degrés des balises ; on le note
D(G).
On se propose d'étudier l'algorithme naïf d'étiquetage
suivant. On considère un ordre sur les balises et on étiquette le
graphe de proche en proche en suivant cet ordre : on définit
j (b) comme étant la plus petite des fréquences non
utilisées dans l'étiquetage des balises voisines de b et la
précédant dans l'ordre.
Question 6.
a) Montrer que n(G) £ D(G)+1.
b) On appelle clique de G un sous-ensemble de balises
tels que deux quelconques d'entre elles soient voisines.
Par exemple, les balises du tétraèdre central du graphe 3 forment
une clique à 4 éléments. On note w(G) la taille
(c'est-à-dire le nombre de balises) de la
plus grande clique de G. Comment se comparent n(G) et w(G) ?
c) Pour tout n, donner un exemple de graphe connexe à n
sommets où la borne supérieure D(G)+1 est atteinte. Pour
quelles valeurs de n existe-t-il un graphe connexe G tel que
D(G) = 2 et n(G)=3 ?
Question 7.
On considère le graphe Gn ayant 2n balises
B = {b0, b1, ... , bn-1, c0, c1, ... , cn-1} et tel
que les voisins de bi sont tous les cj satisfaisant j ¹ i.
a) Quelles sont les fréquences attribuées par
l'algorithme naïf, si les balises sont considérées dans l'ordre :
b0, c0, b1, c1, ... , bi, ci, bi + 1, ... ,
bn-1, cn-1.
b) Quelle est la valeur de n(Gn) ?
À partir de maintenant, on suppose que B est représenté par
l'ensemble des entiers {0, 1, ..., n-1}. La classe Graphe
est alors définie par :
class Graphe{
int n;
Liste[] vois;
int[] freq;
...
}
où vois[i] contient la liste des numéros des balises
voisines de i. La classe Liste implante une liste d'entiers,
comme dans le cours. On pourra utiliser les primitives classiques
associées à cette classe.
Question 8.
Donner la méthode
static void naif(Graphe G)
qui réalise l'algorithme naïf d'attribution de fréquences
avec l'ordre usuel 0 < 1 < 2 < ... < n-1. Si m est le nombre
d'arêtes du graphe G et k le nombre de fréquences utilisées, on
veut que cette méthode soit de coût O(k n + m).
Question 9.
On suppose que les balises se trouvent toutes sur une même
droite du plan euclidien. À chaque balise b est associée un
intervalle Ib = [xb, xb'] qui représente la zone d'influence de
b, c'est-à-dire que b peut émettre vers tout mobile présent
dans cet intervalle. Deux balises sont voisines si et seulement si
leurs intervalles ont une intersection non vide.
a) Dessiner le graphe G des quatre balises a, b, c, d
ayant pour intervalles respectifs : [1, 3], [2, 5], [6, 8], [4,
7]. Donner un ordre de parcours sur les
balises tel que l'algorithme naïf attribue trois fréquences
à G. Que vaut n(G) ?
b) On applique l'algorithme naïf en considérant les
balises dans l'ordre croissant des xb. Montrer que si le nombre de
fréquences attribuées est k, alors le graphe G possède une
clique de taille k. En déduire que dans ce cas l'algorithme
naïf donne l'attribution optimal de fréquences.
c) On se place dans un modèle à deux dimensions. Ainsi
chaque balise peut émettre dans un rectangle [xb, xb'] ×
[yb, yb']. Deux balises sont voisines si leurs rectangles se
coupent. Utiliser l'exemple donné ci-dessus pour montrer que
l'algorithme naïf qui considère les balises dans l'ordre des
xb croissant ne donne pas l'attribution optimale de fréquences.
III. Amélioration de l'étiquetage
Dans cette partie, on s'intéresse à quelques techniques
permettant de diminuer le nombre de fréquences attribuées
par l'algorithme naïf.
Soit G un graphe : on dit que la balise c est accessible
depuis la balise b s'il existe un chemin entre b et c dans le
graphe. Soient f1 et f2 deux fréquences
distinctes de balises. On note H(f1, f2) le sous-graphe
de G dont les balises sont toutes celles ayant une fréquence égale
à f1 ou f2. Pour une balise b de fréquence
f1, ou f2 on note Hb(f1, f2) la composante de H(f1,
f2) contenant b et les balises accessibles à partir de b dans
le graphe H(f1, f2).
On utilise le principe suivant. Soient b et c deux balises de
fréquences distinctes respectives f1 et f2.
On dit que b et c sont égalisables si et seulement si
c n'est pas dans Hb(f1, f2). Dans ce cas, on peut en effet
échanger les fréquences dans Hb(f1, f2) sans que
l'étiquetage de G devienne invalide.
Question 10.
Écrire une méthode
static void echangerFreq(Graphe G, int b, int f1, int f2)
qui échange les fréquences f1 et f2 dans la composante
Hb(f1, f2) pour b donnée de fréquence f1.
On modifie l'algorithme naïf de la façon suivante :
Lors de chaque étape, avant d'attribuer à b
une fréquence nouvelle (i.e., non attribuée à une autre balise
avant b) on examine si elle admet un couple de voisins
égalisables, et dans ce cas on effectue l'échange des fréquences
sur l'une des composantes.
Question 11.
a) Montrer sur le graphe Gn que cette nouvelle
version de l'algorithme donne, avec le même ordre des balises
que celui considéré plus haut, un bien meilleur résultat.
b) Écrire la nouvelle version de l'algorithme sous forme d'une
méthode :
static void naifAmeliore(Graphe G)
de complexité O(n D(G)2).
Question 12.
Soit G un graphe dont le maximum des degrés des sommets
est D. On suppose avoir étiqueté toutes les balises avant la
balise b avec les D fréquences 0, 1, ..., D-1. On suppose que
b a D voisines ayant des fréquences distinctes 0, 1,
..., D-1 et qu'il existe une balise c déjà
considérée, accessible depuis b, et dont les voisines sont
étiquetées avec strictement moins de D-1 fréquences. Montrer
qu'on peut étiqueter b avec une fréquence <D.
On suppose dans la suite du problème que le graphe G est D-régulier, c'est-à-dire que toutes les balises ont degré
D.
Pour deux balises b1 et b2 reliées par un chemin ne contenant
que des balises de fréquence f1=j (b1) et
f2=j (b2), on note F(b1, b2) = Hb1(j (b1),
j (b2)) la composante du graphe formée des balises de
fréquence f1 ou f2.
Question 13.
On se propose de modifier encore l'algorithme naïf afin
d'égaliser deux voisines bi et bj d'une balise b, ce qui
permettra de récupérer à chaque fois une fréquence pour
b. Pour cela on change la valeur de la fréquence de certains
sommets, en utilisant une fréquence déjà attribuée.
Montrer que cela est possible dans chacun des deux cas suivants.
a) Les voisines de b ont toutes des fréquences différentes
et deux d'entre celles-ci b1 et b2 forment une composante
F(b1, b2) qui contient une balise ayant 3
voisines dans la composante.
b) Les voisines de b ont toutes des fréquences différentes
et trois d'entre celles-ci b1, b2, b3 sont telles que F(b1,
b2) et F(b1, b3) ont une balise commune autre que b1.
Question 14.
Montrer que l'on peut rendre égalisables deux
voisines b1 et b2 d'une balise b qui ne sont pas voisines
entre elles dans le cas où il existe une troisième voisine
b3 telle que F(b1, b2), F(b1, b3), et F(b3, b2) n'ont
deux à deux aucune balise commune (autre que b1, b2, b3).
Question 15.
En déduire une preuve du résultat théorique suivant :
tout graphe G qui n'est pas une clique et tel
que D(G) > 2 satisfait n(G) £ D(G).
This document was translated from LATEX by HEVEA.