Contrôle Classant d'Informatique
Promotion 1998
Corrigé rédigé par Georges Gonthier et François Morain
Question 1.
a)
static int distance(int x1, int y1, int x2, int y2){
return Math.abs(x2-x1)+Math.abs(y2-y1);
}
b)
static ListeM estDansListe(ListeM lm, int num){
if(lm == null) return null;
if(lm.num == num) return lm;
else return estDansListe(lm.suiv, num);
}
c)
static int distanceM(ListeM lm, int num1, int num2){
ListeM l1, l2;
l1 = estDansListe(lm, num1);
l2 = estDansListe(lm, num2);
return distance(l1.xm, l1.ym, l2.xm, l2.ym);
}
Question 2.
a)
static int plusPetiteDistance(ListeM lm, int x, int y){
int dmin, d;
if(lm == null) return -1;
dmin = distance(x, y, lm.xm, lm.ym);
for(ListeM l = lm.suiv; l != null; l = l.suiv){
d = distance(x, y, l.xm, l.ym);
if(d < dmin) dmin = d;
}
return dmin;
}
b)
static ListeM plusProches(ListeM lm, int x, int y){
int dmin = plusPetiteDistance(lm, x, y);
ListeM lpp = null;
for(ListeM l = lm; l != null; l = l.suiv){
if(distance(x, y, l.xm, l.ym) == dmin)
lpp = new ListeM(lpp, l.xm, l.ym, l.num);
}
return lpp;
}
Question 3.
a)
static int distanceM2(ListeM[] reg, int num1, int num2){
ListeM l1, l2;
l1 = estDansListe(reg[h(num1)], num1);
l2 = estDansListe(reg[h(num2)], num2);
return distance(l1.xm, l1.ym, l2.xm, l2.ym);
}
b)
On doit parcourir chaque liste tour à tour :
static ListeM plusProches2(ListeM[] reg, int x, int y){
ListeM lpp = null;
int dmin = -1, d;
for(int i = 0; i < reg.length; i++){
for(ListeM l = reg[i]; l != null; l = l.suiv){
d = distance(x, y, l.xm, l.ym);
if((dmin == -1) || (d < dmin)){
dmin = d;
lpp = new ListeM(null, l.xm, l.ym, l.num);
}
else
if(d == dmin)
lpp = new ListeM(lpp, l.xm, l.ym, l.num);
}
}
return lpp;
}
c)
La recherche de mobiles les plus proches prend le même nombre
d'opérations dans les deux cas. Par contre, le coût de recherche
est plus faible : il nécessite le calcul de h(num), puis une
recherche dans une liste qu'on suppose de petite taille.
Question 4.
On parcourt les listes de reg en les coupant en deux à chaque
fois :
static void divise(ListeM[] rega, ListeM[] regb, ListeM[] reg,
int xa, int ya, int xb, int yb){
/* on initialise rega et regb */
for(int i = 0; i < reg.length; i++){
rega[i] = null;
regb[i] = null;
}
for(int i = 0; i < reg.length; i++)
for(ListeM l = reg[i]; l != null; l = l.suiv)
if(distance(xb,yb,l.xm,l.ym)<distance(xa,ya,l.xm,l.ym))
regb[i] = new ListeM(regb[i], l.xm, l.ym, l.num);
else
rega[i] = new ListeM(rega[i], l.xm, l.ym, l.num);
}
Question 5.
Des étiquetages possibles sont :
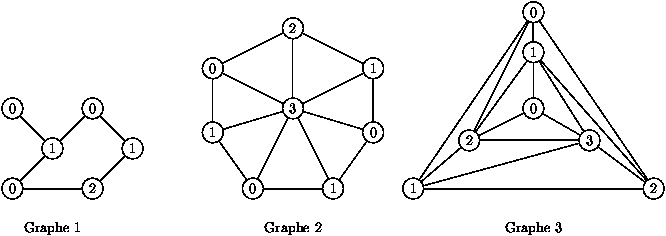
Question 6.
a)
Il suffit de montrer que j (b) £ D(G)+1 pour tout
b. Or, pour chaque b, le nombre de valeurs différentes comprises
dans l'ensemble des fréquences utilisées pour les voisines de b
traitées précédemment est majoré par le nombre de voisines de
b, donc inférieur à D(G).
b)
Une clique contenant k balises a un degré égal à k-1 et
toutes les balises ont k-1 voisins, ce qui implique qu'il faut
exactement k fréquences pour l'étiqueter. Tout graphe contenant
une telle clique a donc besoin d'au moins k fréquences et le
résultat suit. Par suite n(G)³ w(G).
c)
C'est le cas de la clique à n balises. Si D(G)=2
et G est un cycle d'ordre impair, alors n(G) = 3 :
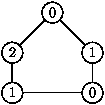
Question 7.
a)
Considérons par exemple le cas n=3 :
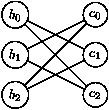
On montre par récurrence que le couple (bi, ci) est
étiqueté avec la fréquence i pour tout i, ce qui conduit
à N(j )=n.
b)
Si n=1, le graphe est réduit à deux points non voisins, donc
n(G1) = 1. Si n>1, la balise b0 a au moins un voisin, donc
il faut au moins deux fréquences. En fait, deux suffisent : on
attribue à tous les bi la fréquence 0 et aux ci la
fréquence 1.
Question 8.
Pour chaque i, on remplit un tableau de booléens utilisee
tel que utilisee[f] vaut vrai si la fréquence f est
utilisée dans l'étiquetage des voisins j de i qui sont <
i. Une fois cela fait, on cherche dans ce tableau la plus petite
valeur égale à faux, qui nous donne la fréquence cherchée. Il
est clair que n(G) £ n, donc un tableau de taille n est
largement suffisant pour utilisee.
static void naif(Graphe G){
boolean[] utilisee = new boolean[G.n];
int j, k = 0;
for(int i = 0; i < G.n; i++){
/* on initialise */
for(j = 0; j <= k; j++)
utilisee[j] = false;
/* on cherche toutes les fréquences utilisées */
for(Liste l = G.vois[i]; l != null; l = l.suiv)
if(l.b < i)
utilisee[G.freq[l.b]] = true;
/* on cherche la plus petite fréquence libre */
for(j = 0; utilisee[j]; j++);
G.freq[i] = j;
if(j == k) k++;
}
}
Question 9.
a)
L'ordre a<c<b<d donne trois fréquences alors que deux suffisent :
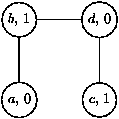
b)
Soit b une balise à qui l'algorithme naïf attribue la
fréquence k. Cela veut dire qu'il existe k-1 intervalles
Ibi = [xbi, xbi'] vérifiant xb1 £
xb2 £ ··· £ xbk-1. Par hypothèse xbk-1
£ xb et de plus [xb, xb'] a une intersection non vide avec
les Ibi, ainsi xb est dans tous les Ibi et donc les
bi et b forment une clique.
c)
On construit le graphe associé aux rectangles [1, 10] × [1,
3], [3, 10] × [6, 8], [5, 13] × [4, 7], [6, 15] ×
[2, 5] de balises a, b, c, d :
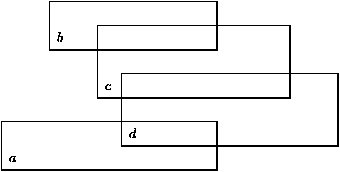
Si on parcourt ce graphe dans l'ordre des xb, l'algorithme naïf lui
attribue trois fréquences (a, 0), (b, 0), (c, 1) forçant
(d, 2) alors que deux suffisent : (a, 0), (d, 1), (c, 0), (b,
1).
Question 10.
On doit chercher une composante connexe du graphe H(f1, f2)
contenant b. Pour cela, on parcourt le graphe G en profondeur
d'abord à partir de la balise b et on échange les fréquences :
/* Ici, on sait déjà que phi(b) = f1 ou f2 */
static void echangerAux(boolean[] visite, Graphe G, int b, int f1, int f2){
if(! visite[b]){
visite[b] = true;
if(G.freq[b] == f1)
G.freq[b] = f2;
else
G.freq[b] = f1;
for(Liste l = G.vois[b]; l != null; l = l.suiv)
if((G.freq[l.b] == f1) || (G.freq[l.b] == f2))
echangerAux(visite, G, l.b, f1, f2);
}
}
/* f1 = freq(b) */
static void echangerFreq(Graphe G, int b, int f1, int f2){
boolean[] visite = new boolean[G.n];
echangerAux(visite, G, b, f1, f2);
}
Question 11.
a)
Nous allons montrer cette fois que pour tout i, (bi, ci) vont
recevoir les fréquences (1, 0). Au départ, b0 reçoit 0
et c0 également. De même, b1 et c1 reçoivent
1. La balise b2 a deux voisines (c0, 0), (c1, 1). Or c0
n'est pas dans Hc1(1, 0) = {(b0, 0)}, donc on peut
reétiqueter cette composante, ce qui attribue 0 à b0 et 1
à c1. Par récurrence, à partir de i = 3, on constate que
toutes les balises cj (resp. bj) pour j<i voisines de bi
(resp. ci) ont reçu la fréquence 0 (resp. 1) et donc
bi reçoit la fréquence 1 (resp. 0).
b)
On gère au plus juste la valeur de la plus grande fréquence
utilisée, appelée ici k :
static void naifAmeliore(Graphe G){
boolean[] utilisee = new boolean[G.n];
int k = 0, j;
for(int i = 0; i < G.n; i++){
/* recherche de la plus petite fréquence non utilisée */
for(j = 0; j <= k; j++)
utilisee[j] = false;
for(Liste l = G.vois[i]; l != null; l = l.suiv)
if(l.b < i)
utilisee[G.freq[l.b]] = true;
/* on cherche la plus petite fréquence libre */
for(j = 0; utilisee[j]; j++);
if(j <= k)
/* pas besoin d'une nouvelle fréquence */
G.freq[i] = j;
else{
/* égalisons si c'est possible */
boolean egalise = false;
int f1 = -1, f2 = -1;
for(Liste lb=G.vois[i]; (lb!=null) && !egalise; lb=lb.suiv)
if(lb.b < i)
for(Liste lc=lb.suiv; (lc!=null) && !egalise; lc=lc.suiv)
if((lc.b < i) && (G.freq[lc.b] != G.freq[lb.b])){
f1 = G.freq[lb.b];
f2 = G.freq[lc.b];
echangerFreq(G, lb.b, f1, f2);
if(G.freq[lc.b] != f2)
/* raté, lc.b était dans H[lb.b] */
echangerFreq(G, lb.b, f2, f1);
else
egalise = true;
}
if(egalise)
G.freq[i] = f1;
else{
k++;
G.freq[i] = k;
}
}
}
}
Pour chaque balise i, on doit examiner au plus d(i) (d(i)-1)/2 couples
de balises voisines distinctes (b, c). Le calcul de Hb(j (b),
j (c)) demande un parcours de G, donc au plus 2m
opérations. Le coût est donc borné par O(n k)+O(n
(D(G)2+m)) = O(n D(G)2).
Question 12.
Considérons le chemin [b, c], qui passe par les balises b0 = b,
b1, b2, ..., br-1, br = c. On commence par enlever
toutes les étiquettes de bi pour 0 < i £ r, puis on utilise
l'algorithme naïf pour étiqueter b0, b1, ..., br
dans cet ordre. La balise b0 se trouve avoir D-1 voisines de
fréquences distinctes, il en reste une <D pour b0. Tant que i
< r, la balise bi a au plus D-1 voisines étiquetées, donc on
peut lui attribuer une fréquence <D. La balise br = c a
strictement moins de D-1 voisines, donc il reste encore une
fréquence <D pour c.
Question 13.
a)
Soit c la première balise rencontrée sur le chemin de b1 à
b2 ayant trois voisines de même fréquence f dans la
composante F(b1, b2) :
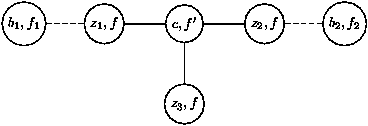
On peut donc réétiqueter c avec une fréquence
non utilisée f'' < D, ce qui scinde la composante connexe liant b1 à
b2. On peut donc égaliser (b1, f1) et (c, f'') ce qui
permet de libérer f1 pour la donner ultérieurement à b.
b)
Appelons y la balise commune. Elle a quatre voisines étiquetées
avec deux fréquences seulement. On peut donc trouver une autre
fréquence <D non encore utilisée f'' pour y, ce qui permet de
séparer encore une fois b1 et b2 et on peut égaliser (b1,
f1) et (y, f''), libérant f1 pour b.
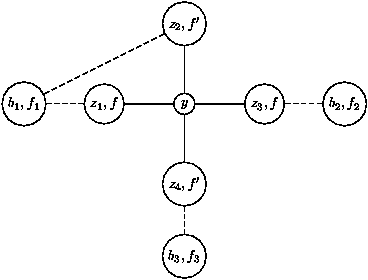
Question 14.
Remarquons tout d'abord qu'on peut supposer qu'il n'existe qu'un
chemin de b1 à b2 dans F(b1, b2) (de même pour les
autres balises). En effet, s'il existait deux chemins, b1 aurait
deux voisines de même fréquence f2, donc on pourrait appliquer
la question 12.
Soit y le premier sommet rencontré dans le chemin allant de
b1 à b2 dans F(b1, b2). Il est nécessairement de
fréquence f2 et différent de b2, car b1 et b2 ne sont
pas voisines. On égalise (b1, f1) et (b3, f3). Deux cas peuvent se
produire : si l'égalisation ne crée pas de chemin de (b1, f3)
vers (b2, f2) dans la composante F'(b1, b2) du nouveau
graphe, on égalise (b1, f3) et (y, f2) et on a réussi à
égaliser b1 et b2. Si l'égalisation a créé un nouveau
chemin de b1 vers b2, les deux composantes F'(b1, b2) et
F'(b1, b3) ont un sommet commun et on peut appliquer la question
précédente.
Donnons un exemple illustrant le premier cas :
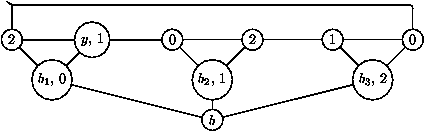
Les deux balises b1 et b2 ne sont pas adjacentes.
On égalise b1 et b3, ce qui donne :
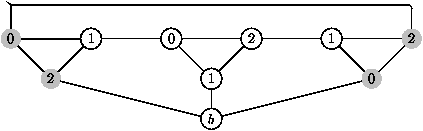
puis on égalise b1 et y :
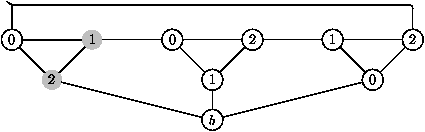
ce qui permet d'attribuer la fréquence f2 = 2 à la balise b.
Pour le second cas, considérons :
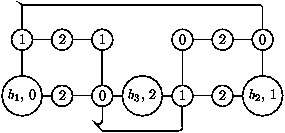
L'égalisation de b1 et b3 crée un nouveau chemin entre b1
et b2 :
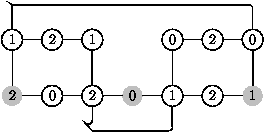
Question 15.
Raisonnons par récurrence sur le couple (D, n) avec D³ 3. On
suppose la propriété vraie pour tout graphe G de degré
D(G) £ D et n' < n.
Soit donc G de degré D et nombre de sommets n. D'après la
question 12, il suffit de considérer le cas où G est
D-régulier. De même, on peut supposer G connexe, quitte à
raisonner sur chacune de ses composantes connexes. Soit b une balise
de G. On considère le graphe G' obtenu en enlevant b.
Supposons d'abord D(G') < D(G). Si 3 £ D(G') <
D(G), l'hypothèse de récurrence nous dit que l'on peut
étiqueter G' avec au plus D(G') £ D(G)-1
fréquences : il restera donc une fréquence de libre pour
l'attribuer à b et on étiquette G avec au plus D(G)-1+1
fréquences, ce qui prouve le résultat.
Si D(G')=2, on sait que l'on peut étiqueter G' avec deux
fréquences si G' ne contient pas de cycle de longueur impaire et
trois sinon. Dans les deux cas, on a étiqueté G' avec au plus
D(G) fréquences.
Supposons maintenant D(G') = D(G) ³ 3. Le graphe G' n'est
pas une (D+1)-clique, car les voisines de b sont de degré <D
dans G'. On peut étiqueter G' avec au plus D(G') =
D(G) fréquences par hypothèse de récurrence.
Soient b1, b2, ..., bD les balises voisines de b dans
G. Soit c l'une des balises de G - {b, b1, b2, ..., bD
}. Si les voisines de c sont étiquetées avec moins de D-1
fréquences, on applique la question 12.
On choisit alors deux balises bi et bj
non adjacentes (ce qui est possible car G n'est pas une
D+1-clique). S'il existe une balise bk telle que F(bi, bk) et
H(bj, bk) aient un point commun, on applique la question
13b. Sinon, on applique 14.
This document was translated from LATEX by HEVEA.











