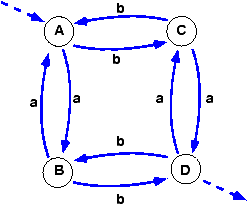
Planche 1

Inf 431 -- Cours 14
Grammaires formelles
http://jeanjacqueslevy.net
secrétariat de l'enseignement:
Catherine Bensoussan
cb@lix.polytechnique.fr
Aile 00, LIX,
01 69 33 34 67
http://www.enseignement.polytechnique.fr/informatique

Planche 2

Plan

La classification de Chomsky
Langages réguliers et expressions régulières
Analyse syntaxique des langages algébriques généraux
Langages récursivement énumérables

Planche 3

Langage régulier (rationnel)

Nombre impair de a et nombre impair de b

A ® aB

A ® bC

B ® aA

B ® bD

B ® b

C ® aD

C ® bA

C ® a

D ® aC

D ® bB

Exemple de dérivation:

A

® a

B

® aa

A

® aab

C

® aaba

D

® aabaa

C

® aabaaa

Planche 4

**Langage algébrique (context-free)**

langage { aⁿ bⁿ | n > 0 }

S ® a S b S ® ab

Exemple de dérivation:

S

® a

S

bS ® aa

S

bbS ® aaa

S

bbb ® aaaabbbb
système de parenthèses

S ® a S b S S ® abS S ® aSb S ® ab

Exemple de dérivation:

S

® a

S

bS ® aa

S

bbS ® aaabbb

S

® aaabbba

S

b ® aaabbbaabb
automates à pile [Chomsky, Schutzenberger]
On rajoute une pile au fonctionnement d'un automate fini
Par exemple pour { a ⁿ bⁿ | n > 0 }.

Table de transitions (q₁ état initial, Z dans la pile, F = { q₄ })

a,Z a,X b,X e,Z

q₁ (q₂, ZX)

q₂ (q₂, XX) (q₃, e)

q₃ (q₃, e) (q₄,Z)

q₄

Planche 5

Langage context-sensitive

langage { a ⁿ bⁿ cⁿ | n > 0 }

S ® e	S ® A
A ® aABC	CB ® BC	aB ® ab	bC ® bc
A ® aBC		bB ® bb	cC ® cc

Exemple de dérivation:

® a

BC ® aa

BCBC ® aaaB

CBC

® aaaBBC

C ® aaaBB

CC ® aa

BBCCC

® aaa

BCCC ® aaab

CCC ® aaabb

® aaabbb

C ® aaabbbc

® aaabbbccc

Le contexte intervient; les dérivations ne font pas décroitre la taille des mots.

Exercice 1 Donner une grammaire pour les langages suivants:

· { aⁿbⁿcⁿdⁿ\| n > 0 }	· { a^n² \| n ³ 0 }
· { uu \| u Î S^* }	· { aⁿbⁿc^p \| n ³ 0, p ³ 0 } È { aⁿb^pc^p \| n ³ 0, p ³ 0 }

Planche 6

Langages et Grammaires

Un langage L est un ensemble de mots sur l'alphabet S (L Ì S^*).

Une grammaire est un 4-uplet G = (S, V_N, S, P)

S alphabet des symboles terminaux
V_N ensemble de non terminaux, V = S È V_N
S Î V_N axiome
P ensemble fini de règles de productions de la forme a_i ® b_i (a_i Î V⁺ - S⁺, b_i Î V^*)

Planche 7

Classification de Chomsky

type	forme des productions		catégorie
0	a ® b	a Î V⁺-S⁺, b Î V^*
1	a ® b	aÎ V⁺ - S⁺, b Î V⁺, \|a\| £ \|b\|	*context sensitive*
2	A ® b	A Î V_N, b Î V⁺	*context-free*
3	A ® aB	A,B Î V_N, a Î S	régulier
	A ® a

Une exception est possible pour l'axiome S, qui peut figurer dans une règle S ® e à condition de ne pas apparaître dans une partie droite de production.

Planche 8

Langage généré par une grammaire

Une dérivation élémentaire ua v ¾® ub v s'obtient par application d'une règle a ® b de production.

Une dérivation u ¾®^* v est une suite de dérivations élémentaires u=u₀ ¾® u₁ ¾® u₂ ... u_n=v (n ³ 0)

Le langage généré par une grammaire G = (S, V_N, S, P) est:

L(G) = { u | S ¾®^* u Î S ^* }

Un langage est de type i s'il existe une grammaire de type i qui le génère (0 £ i £ 3 ). Soit L_i les langages de type i sur S.

Comme G de type i+1 implique G de type i, on a L₃ Ì L₂ Ì L₁ Ì L₀.

Planche 9

Notations abrégées

Souvent on factorise les productions qui ont une même partie gauche grâce au (méta)symbole | (barre verticale):

a ® b₁ | b₂ | ... b_n

pour

a ® b₁ a ® b₂ ...a ® b_n

Une autre notation fréquente est proche de la BNF (Backus Naur Form), la flèche est remplacé par ``::='':

a ::= b₁ | b₂ | ... b_n

Par exemple, l'espace des termes t est défini par

t ::= t + t | t * t | t - t | t / t | nb

qui ressemble à une définition récursive. Parfois on duplique les symboles non terminaux pour distinguer les occurences dans les parties droites:

t,t' ::= t + t' | t * t' | t - t' | t / t' | nb

Planche 10

Langage régulier et automate fini

Théorème 1Un langage est régulier si et seulement s'il est généré par un automate fini.

Démonstration: Si G est la grammaire (de type 3) générant L, on considère l'automate non-déterministe A=(S, V_N, S, {q_f}, d) tel que

B Î d(A, a) si A ® aB
q_f Î d(A, a) si A ® a

Alors T(A) = L(G).

Réciproquement, si L=T(A) et A=(S, Q, q₀, F,d), on considère la grammaire G = (S, Q, q₀, P) telle que

A ® aB si B Î d(A, a)
A ® a si d(A,a) Ç F ¹ Ø

Alors L(G) = T(A).

Planche 11

Expression régulière et automate (1/5)

En admettant l'équivalence entre automates finis avec ou sans e-transitions, on suppose que les automates finis n'ont qu'un seul état de fin q_f avec d(q_f,a) = Ø pour tout a Î S. De même, on peut supposer q₀ Ïd(q,a) pour tout qÎ Q et a ÎS.

Alors les automates finis reconnaissent les expressions régulières par les constructions suivantes.

Planche 12

Expression régulière et automate (2/5)

Construction due à [Thompson] (l'inventeur du système Unix!).

Planche 13

Expression régulière et automate (3/5)

Théorème 2[Kleene] Un langage est régulier si et seulement s'il est décrit par une expression régulière.

Démonstration: Par la construction précédente, on montre par récurrence sur la taille de l'expression régulière que toute expression régulière est reconnue par un automate.

Réciproquement, supposons les n états de A=(S, Q, q₀, F) numérotés dans 0, 1, ...n-1. Soit L_i,j^k l'ensemble des mots permettant d'aller de q_i à q_j en passant par des états strictement inférieurs à k. Alors

L_i,i⁰ = {e} È {a | d(q_i, a) = q_i }

L_i,j⁰ = {a | d(q_i, a) = q_j }

L_i,j^k+1 = L_i,j^k È L_i,k^k (L_k,k^k)^* L_k,j^k

Et L=T(A) = È_{q_iÎ F} L_0,iⁿ.

Planche 14

Expression régulière et automate (4/5)

Pour (a+b)^*ab, l'automate est:

En supprimant les e-transitions et en déterminisant, on obtient:

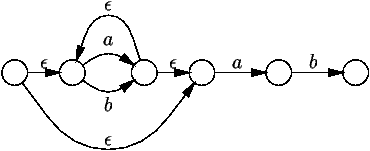
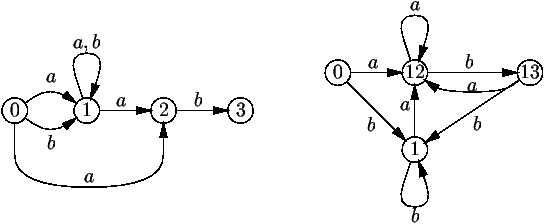
Planche 15

Expression régulière et automate (5/5)

L'automate obtenu par la construction précédente est non-déterministe, il a beaucoup de e-transitions.
On peut toujours déterminiser l'automate obtenu, et considérer l'automate minimal.
Il existe des constructions plus directes pour obtenir de bons automates (peut-être pas minimaux) [Glushkov; Brzozowski; Berry-Sethi; Berstel-Pin] en considérant les expressions régulières linéaires, et les expressions régulières dérivées.

Planche 16

Mot vide dans une grammaire algébrique

Les productions A ® a doivent avoir une partie droite non vide (a ¹ e) à l'exception de l'axiome.

Or, dans le cours 4, on avait autorisé (par exemple) S ® aSbS, S ® e.

Mais les deux définitions de grammaires algébriques génèrent les mêmes langages algébriques.

En effet, si on a B ¾®^* e et une règle A ® a B b, on ajoute la règle A ® ab. Puis on supprime toutes les productions A ® e. Et si on avait S ¾®^* e, on considère un nouvel axiome S' et on ajoute les nouvelles règles S' ® e et S' ® S.

Sur l'exemple précédent, cela donne successivement

S ® aSbS	S ® e	S ® abS	S ® aSb	S ® ab
S' ® e	S' ® S	S ® aSbS	S ® abS	S ® aSb	S ® ab

Exercice 2 Supprimer les parties droites vides dans ces deux grammaires vues au cours 4

S ® e	S ® S S S ® a S b
A ® e	A ® `[` A nb A `]`

Planche 17

Forme normale de Chomsky

Toute grammaire algébrique a une grammaire équivalente dont les règles sont de la forme A ® a, A ® BC (a Î S), à l'exception de l'axiome qui peut avoir une règle S ® e.

En effet, on peut trouver toutes les non-terminales B et C telles que B ¾®^* C. Ensuite, si on a A ® a B b avec C ® g et |g| ³ 2, on ajoute la règle A ® agb. Puis on supprime toutes les règles A ® B.

A présent toutes les règles sont de la forme S ® e, A ® a, A ® a avec |a|³ 2.

Pour chaque production A ® a= X₁X₂... X_n, on ajoute de nouvelles non-terminales Y_i et on pose

Y_i ® X_i quand X_i Î S
A ® X₁Y₂ Y₂ ® X₂Y₃ ...Y_n-1 ® X_n-1X_n.

Exercice 3 Mettre en forme normale de Chomsky les grammaires de l'exercice précédent.

Planche 18

Langage récursivement énumérable

Théorème 3Un langage est de type 0 (dans la classification de Chomsky) ss'il est récursivement énumérable.

Démonstration: D'abord si un langage est de type 0, on peut construire une machine de Turing qui le génère.

Réciproquement, supposons qu'un langage L vérifie L=T(M) avec M = (Q, S, G, d, q₀,B, F) est une machine de Turing. On construit la grammaire G=(SÈ {$}, Q È G È {S,S'}, S, P) avec comme productions:

qX ® Yp si (u,q,Xv) ¾® (uY,p,v)
q$ ® Yp$ si (u,q,e) ¾® (uY,p,e)
ZqX ® pZY si (uZ,q,Xv) ¾® (u,p,ZY)
Zq$ ® pZY$ si (uZ,q,e) ¾® (u,p,ZY)
S ® q₀S'
S' ® a S'
S' ® $

Alors u$ Î L(G) ssi u Î T(M).

Planche 19

Quelques exercices

Exercice 4 Montrer qu'il existe un algorithme pour reconnaître un langage contexte-sensitif, c'est-à-dire répondant oui si le mot d'entrée est dans le langage, et non s'il n'appartient pas.

Exercice 5 Montrer qu'il n'existe qu'un semi-algorithme pour reconnaître un langage récursivement énumérable, c'est-à-dire répondant oui si le mot d'entrée est dans le langage.

Exercice 6 Montrer qu'il existe une analyse descendante fonctionnant pour tout langage algébrique, mais avec retours en arrière (backtracking) dans le mot d'entrée. Complexité?

Exercice 7 Quel est la notion d'arbre syntaxique pour les langages non algébriques?

Exercice 8 Montrer que l'intersection n'est pas forcément close sur les langages algébriques.

Exercice 9 Donner un algorithme pour trouver les non-terminales A telles que A ¾®^* e dans un langage algébrique.

Exercice 10 Donner un algorithme pour trouver les non-terminales A telles que A ¾®^* B (B Î V_N) dans un langage algébrique.

This document was translated from L^AT_EX by H^EV^EA.

· { aⁿbⁿcⁿdⁿ\| n > 0 }	· { a^n² \| n ³ 0 }
· { uu \| u Î S^* }	· { aⁿbⁿc^p \| n ³ 0, p ³ 0 } È { aⁿb^pc^p \| n ³ 0, p ³ 0 }

	a,Z	a,X	b,X	e,Z
q₁	(q₂, ZX)
q₂		(q₂, XX)	(q₃, e)
q₃			(q₃, e)	(q₄,Z)
q₄