Solution de systèmes polynomiaux par homotopie
Éric Schost, LIX, École polytechnique
Eric.Schost[at]polytechnique.fr |
Vue d'ensemble
Le but de ce projet est de “résoudre” des systèmes de n
équations polynomiales de degré 2 à n inconnues (un tel
système a généralement 2n solutions). Il s'agit de mettre en
place un cas particulier simplifié de ce qu'on appelle méthodes par homotopie.
Résoudre un système F=F1,...,Fn dans
k[X1,...,Xn] (k est un corps pour l'instant quelconque)
reviendra à calculer des polynômes à une variable
P,V2,...,Vn tels que l'ensemble des solutions de F=0 soit
décrit par
⎧
⎪
⎨
⎪
⎩ |
| P(X1) |
= |
0 |
| X2 |
= |
V2(X1) |
| |
⋮ |
|
| Xn |
= |
Vn(X1); |
|
|
Pour calculer la résolution, on commence par définir un système
G de référence. L'objectif est de pouvoir résoudre G “à
vue” ; on prend donc G1 = X12−X2, G2 = X22 − X3,
..., Gn−1 = Xn−12−Xn, Gn = Xn2−1.
Il est très
facile de résoudre ce système sur le modèle ci-dessus ; on
obtient
⎧
⎪
⎨
⎪
⎩ |
| X12n |
= |
1 |
| X2 |
= |
X12 |
| |
⋮ |
|
| Xn |
= |
X12n−1. |
|
|
F1ε= ε F1 + (1− ε) G1,
... , Fnε= ε Fn + (1−ε)
Gn,
En faisant ε = 1, on retrouve F ; en faisant
ε =0, on retrouve G. Ceci mène à l'algorithme
suivant :
-
On résout le système en ε=0 : on a vu que c'est
immédiat.
- On en déduit une solution “paramétrée par ε”
du système Fε. Cette solution s'écrit
⎧
⎪
⎨
⎪
⎩ |
| Pε(X1) |
= |
0 |
| X2 |
= |
V2ε(X1) |
| ⋮ |
| Xn |
= |
Vnε(X1), |
|
|
- On fait ε=1 dans la solution paramétrée.
Graphiquement, on cherche à déterminer les points de droite, à
partir des points de gauche, en “calculant” une description
des courbes qui les relient.
C'est bien entendu la seconde étape qui pose toutes les
difficultés, et sur laquelle porte l'essentiel du projet.
Calcul de la solution paramétrée
Avant de donner les détails de l'algorithme, on présente
rapidement les structures et les outils dont on aura besoin.
Séries formelles sur k.
Une série formelle à coefficients dans k est une “somme
formelle” de la forme Σi ≥ 0 ai εi ; on note
l'ensemble de ces séries sous la forme k[[ε]].
Ces séries se comportent comme des polynômes pour les
opérations d'addition et de multiplication. Concrètement, on
manipule uniquement des séries tronquées, c'est-à-dire
avec un nombre fini de termes. On introduit donc une notion de
précision : la série a=Σi=0n−1 ai
εi sera dite de précision n. Quand on ajoute ou on
multiplie deux séries tronquées, on effectue l'opération
comme pour des polynômes, puis on tronque le résultat à la
précision courante.
Une différence importante entre séries et polynômes est la
possibilité d'inverser une série formelle dont le terme
constant n'est pas nul. Par exemple, l'inverse de la série
1−ε est la série Σi ≥ 0 εi. La
formule suivante donne l'inverse de la série a = Σi ≥ 0
ai εi : on pose b0 = 1/a0 et
bi+1 = 2 bi − a bi2 mod ε2i+1
pour i ≥ 0. Alors bi est l'inverse de a modulo
ε2i.
Approximation de Padé.
Le second outil dont
on a besoin est le calcul d'approximants de Padé. Si f=p/q
est une fraction rationnelle dans k(ε), le calcul
d'inverse ci-dessus permet de calculer le développement de Taylor de
f en 0. L'approximation de Padé permet de faire l'inverse : si
on connaît le développement de Taylor de f avec suffisamment de
termes (degp +degq+1, en l'occurence), on peut retrouver p et
q (à une constante près). L'algorithme est simple à implanter,
c'est une variante de l'algorithme d'Euclide, il est donné au
chapitre 5 de Modern Computer Algebra, J. von zur Gathen et
J. Gerhard, Cambridge University Press, 1999.
Solutions en séries.
On fait désormais l'hypothèse que le polynôme X12n −1 a
toutes ses racines dans k (on verra plus bas des situations où
c'est le cas). Dans ce cas, il est possible d'expliciter toutes les
solutions du système G. À partir de ces solutions, on va
calculer des solutions sous forme de séries formelles en
ε pour le système Fε.
Comme pour l'inverse, on travaille itérativement. On se donne une
solution initiale x0=(x10,...,xn0) pour Fεmod ε, c'est à dire G. On peut alors calculer la suite
xi=(x1i,...,xni), où chaque xji est une série
à précision 2i, et telle que Fε(xi)=0 modulo
ε2i. On vérifie facilement que la suite définie
par
xi+1 = xi − J(xi)−1 Fε(xi) mod
ε2i+1
convient. Ici, J est la matrice
jacobienne du sysème Fε par rapport à
X1,...,Xn, J(xi) est son évaluation en xi, et
J(xi)−1 l'inverse de celle-ci. Remarquer qu'il s'agit ici d'une
version formelle de l'opérateur de Newton, qui généralise ce
qu'on a écrit pour l'inverse d'une série.
Solutions paramétrées.
On a maintenant tous les outils
nécessaires. La première chose à faire est de calculer toutes
les solutions de G ; c'est immédiat, en utilisant l'hypothèse
qu'on connaît toutes les racines de X12n −1. Il y a 2n
solutions.
En utilisant l'opérateur de Newton, on calcule 2n solutions en
séries formelles de Fε, en allant jusqu'à la
précision 2n+1+1. On va noter x(1),...,x(2n) ces
solutions, où x(i)=(x1(i),...,xn(i)).
On peut d'ores et déjà en déduire le polynôme
Pε. On calcule pour cela le polynôme dont les racines
sont les x1(i). Il est facile de voir que ce polynôme
coïncide “presque” avec Pε : ses coefficients sont
les développements de Taylor à précision 2n+1+1 de ceux de
Pε. Par ailleurs, on peut montrer que les coefficients de
Pε ont des numérateurs et dénominateurs de degrés
au plus 2n. Donc pour retrouver Pε, on calcule un
approximant de Padé de chacun des coefficients, en prenant comme
degré maximal pour les numérateurs et dénominateurs 2n.
Un léger problème se pose pour les polynômes Vε :
leurs coefficients (dans k(ε)) ont des degrés de l'ordre
de 4n, ce qui est beaucoup trop. Pour contourner cette
difficulté, on définit Wjε = (Vjε ×
(Pε)') mod Pε, qui vit aussi dans
k(ε)[X1], et on montre que ce choix est le bon : les
coefficients de Wjε ont un degré au plus en 2n.
Par ailleurs, on voit facilement que Wjε(X1) vaut
si on calcule “à précision infinie”. On
commence donc par calculer cette expression avec des coefficients dans
k[[ε]] à précision 2n+1+1, et on en déduit les
coefficients de Wjε par approximation de Padé en
degré 2n. On fait alors ε=0 dans Wjε
pour obtenir un Wj, et on retrouve Vj par la formule
Wj = (Vj × P') mod P (ce dernier calcul nécessite
un pgcd étendu).
Racines de l'unité dans k.
Ce qui précède demande d'avoir certaines racines de l'unité dans
k. Un choix naturel est alors de travailler dans un corps fini de la
forme 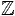 /p
/p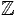 , avec p un premier bien choisi. En
effet, si p est un premier de la forme ℓ 2n +1, on peut
montrer que X2n−1 a toutes ses racines dans k.
, avec p un premier bien choisi. En
effet, si p est un premier de la forme ℓ 2n +1, on peut
montrer que X2n−1 a toutes ses racines dans k.
Par exemple, on pourra prendre p=29 ⋅257+1 et ω = 21.
Alors, ω est une racine 257-ième de 1 dans
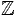 /p
/p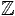 . Dans ce cas, pour tout n ≤ 57, on pose
τ = ω257−n ; les racines de X2n−1 sont les
puissances 1,τ,...,τ2n−1, et elles sont distinctes.
. Dans ce cas, pour tout n ≤ 57, on pose
τ = ω257−n ; les racines de X2n−1 sont les
puissances 1,τ,...,τ2n−1, et elles sont distinctes.
Exemple
On choisit n=2, on travaille modulo 9001, et le système à
résoudre est
F1=8996X22 + 66X2X1 + 99X2 + 77X12 + 54X1 + 8940 = 0,
F2=31X22 + 8989X2X1 + 8975X2 + 8951X12 + 8983X1 + 8939=0.
Modulo 9001, on les a 4 racines quatrièmes de l'unité 1,
9000,1237,7764. On en déduit que les solutions de G:
{X12−X2,X22−1}
sont
( 1, 1 ),
( 9000, 1 ),
( 1237, 9000 ),
( 7764, 9000 ).
En partant de (1,1), on obtient successivement par l'opérateur
de Newton les solutions de Fε en “séries
tronquées”, jusqu'à la précision 9 :
(
1 + 6670ε
,
1 + 4569ε
)
(
1 + 6670ε + 4674ε2 + 8487ε3
,
1 + 4569ε + 4028ε2 + 1959ε3
)
| ( 1 + 6670ε + 4674ε2 + 8487ε3 + 6058ε4 + 4716ε5 +
1854ε6 + 1415ε7, |
| 1 + 4569ε + 4028ε2 + 1959ε3 + 5533ε4 + 4596ε5 +
5107ε6 + 1568ε7) |
| ( 1 + 6670ε + 4674ε2 +
8487ε3 + 6058ε4 + 4716ε5 +
1854ε6 + 1415ε7 + 8903ε8, |
| 1 + 4569ε + 4028ε2 + 1959ε3 +
5533ε4 + 4596ε5 + 5107ε6 +
1568ε7+ 840ε8) |
| |
|
X14 + (96ε + 2400ε2 + 5521ε3 +
82ε4 + 3518ε5 + 3262ε6 +
8605ε7+
+ 5763ε8 )X13 |
| |
|
+ (8793ε + 7463ε2 +
7042ε3 + 6137ε4 + 789ε5 +
3829ε6 + 4951ε7 + 5255ε8)X12 |
| |
|
+ (114ε + 5848ε2
+ 3466ε3 + 8386ε4 + 2077ε5 +
4952ε6 + 364ε7 + 4994ε8)X1 |
| |
|
+ 9000 + 321ε +
5223ε2 + 1843ε3 + 5697ε4 +
4214ε5 + 7588ε6 + 3976ε7 +
2096ε8. |
| X14 |
|
| +
|
| 2346ε4 + 2660ε3 + 3938ε2 +
4726ε |
|
| ε4 + 976ε3 +
1411ε2 + 5186ε + 2487 |
|
X13 |
|
| |
|
| + |
| 2916ε4 + 8872ε3 + 1851ε2 +
4762ε |
|
| ε x4 + 976ε3 +
1411ε2 + 5186ε + 2487 |
|
X12 |
|
| |
|
| + |
| 1207ε4 + 8180ε3 + 4499ε2 +
4487ε |
|
| ε4 + 976ε3 +
1411ε2 + 5186ε + 2487 |
|
X1 |
|
| |
|
| + |
| 4696ε4 + 6406ε3 + 8269ε2
+ 1053ε + 6514 |
|
| ε4 + 976ε3 +
1411ε2 + 5186ε + 2487 |
|
|
| (152ε + 3151ε2 + 7932ε3 +
2801ε4 + 6656ε5 + 8728ε6 +
667ε7 + 5977ε8 )X13 |
| +
(8923ε + 1644ε2 + 2127ε3 + 3934ε4 + 8030ε5 + 4864ε6 +
170ε7 + 5966ε8)X12 |
| + (4 + 8421ε + 2873ε2 + 1813ε3 +
1603ε4 + 998ε5 + 1190ε6 +
1118ε7 + 3333ε8)X1 |
| + 120ε + 1936ε2 + 2120ε3 +
5755ε4 + 8628ε5 + 1888ε6 +
4008ε7 + 2380ε8. |
| |
|
| 3998ε4 + 8412ε3 + 1851ε2 +
8983ε |
|
| ε4 + 976ε3 +
1411ε2 + 5186ε + 2487 |
|
X13 + |
|
| |
|
| 6475ε4 + 6053ε3 + 2711ε2 +
4036ε |
|
| ε4 + 976ε3 +
1411ε2 + 5186ε + 2487 |
|
X12 + |
|
| |
|
| 8732ε4 + 6768ε3 + 2455ε2 +
442ε + 947 |
|
| ε4 + 976ε3 +
1411ε2 + 5186ε + 2487 |
|
X1+ |
|
| |
|
| 693ε4 + 136ε3 + 548ε2 +
1407ε |
|
| ε4 + 976ε3 +
1411ε2 + 5186ε + 2487 |
|
. |
|
⎧
⎨
⎩ |
| X14 + 7910X13 + 1877X12 + 5851X1 + 3439 =0, |
| X2 = 4359X13 + 2251X12 + 2523X1 + 5498. |
|
En factorisant le premier polynôme, on trouve par exemple que
(2353,5333) et (2334,4888) sont solutions du système (F1,F2).
Ce document a été traduit de LATEX par HEVEA


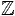 /p
/p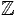 , avec p un premier bien choisi. En
effet, si p est un premier de la forme ℓ 2n +1, on peut
montrer que X2n−1 a toutes ses racines dans k.
, avec p un premier bien choisi. En
effet, si p est un premier de la forme ℓ 2n +1, on peut
montrer que X2n−1 a toutes ses racines dans k.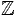 /p
/p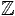 . Dans ce cas, pour tout n ≤ 57, on pose
τ = ω257−n ; les racines de X2n−1 sont les
puissances 1,τ,...,τ2n−1, et elles sont distinctes.
. Dans ce cas, pour tout n ≤ 57, on pose
τ = ω257−n ; les racines de X2n−1 sont les
puissances 1,τ,...,τ2n−1, et elles sont distinctes.