Démontrer automatiquement des petits théorèmes, mini-Prolog
David Monniaux |
Qui, essayant de démontrer un théorème mathématique, n'a jamais eu
recours à la technique d'essayer d'appliquer tous les théorèmes ayant
la bonne conclusion ? Il s'agit ici de faire un mini-prouveur de
théorèmes se basant sur ce principe, appliqué selon la méthode dite de
résolution.
1 Définitions et exemples
1.1 Définitions
On dispose d'un certain nombre de règles de déduction ou
axiomes de la forme :
|
∀ x1 ∀ x2 ... ∀ xn
H1 |
⎛
⎝ |
t11(x1, ..., xn), ..., t1o1(x1, ..., xn) |
⎞
⎠ |
|
∧ ... ∧
Hm |
⎛
⎝ |
tm1(x1, ..., xn), ..., tmom(x1, ..., xn) |
⎞
⎠ |
|
⇒ C |
⎛
⎝ |
t1(x1, ..., xn), ..., to(x1, ..., xn) |
⎞
⎠ |
(1)
Les Hi sont les hypothèses de la règle, C est la
conclusion. Il n'est pas obligatoire que chacune des variables
xj interviennent dans toutes les hypothèses et dans la conclusion.
L'ensemble des hypothèses peut être vide.
Les ti sont des termes. Un terme désigne soit une variable,
soit l'application d'un symbole de fonction à des termes. Nous
ne chercherons pas à attacher un sens aux symboles de fonctions et aux
termes, il suffira donc de les traiter comme des entités syntaxiques
formelles. Une fonction avec zéro paramètres est une constante.
1.2 Exemple : monoïdes
La théorie des monoïdes (version simplifiée des groupes,
sans inverse; par exemple, le monoïde (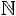 ,+) des entiers naturels)
s'exprime par les axiomes :
,+) des entiers naturels)
s'exprime par les axiomes :
|
|
| ∀ x x = x.e |
|
|
(2) |
| ∀ x x = e.x |
|
|
(3) |
| ∀ x1 ∀ y1 ∀ x2 ∀ y2
x1=x2 ∧ y1=y2 ⇒ x1.y1 = x2.y2 |
|
|
(4) |
| ∀ x ∀ y ∀ z (x.y).z = x.(y.z) |
|
|
(5) |
| ∀ x x=x |
|
|
(6) |
| ∀ x∀ y y=x ⇒ x=y |
|
|
(7) |
| ∀ x∀ y∀ z x=y ∧ y=z ⇒ x=z
|
|
|
(8) |
|
Pour une meilleure compréhension, pensons en termes d'entiers
naturels. 2 + (3 + 5) et 10 sont deux termes syntaxiquement
différents. Toutefois, on peut définir une relation = (l'égalité au
sens mathématique sur les entiers représentés par ces termes)
sur ces termes, qui est une relation d'équivalence compatible avec l'opération + : par exemple,
puisque 2 + (3 + 5) = 10, alors (2 + (3 + 5)) + 6 = 10 + 6.
Nous traduisons ces formules en forme préfixe, afin d'avoir une
syntaxe proche du langage Prolog. P1 ∧ ... Pn ⇒ P
est remplacé par P :- P1, ..., Pn.
egal(X, mul(X, e)).
egal(X, mul(e, X)).
egal(mul(X1, Y1), mul(X2, Y2)) :- egal(X1, X2), egal(Y1, Y2).
egal(mul(mul(X, Y), Z), mul(X, mul(Y, Z))).
egal(X, X).
egal(X, Y) :- egal(Y, X).
egal(X, Z) :- egal(X, Y), egal(Y, Z).
1.3 Exemple : relations familiales
Suivant la même syntaxe, quelques données sur les derniers rois de
France Valois et le premier roi Bourbon (Henri IV).
homme(X) :- estLePereDe(X, Y).
femme(X) :- estLaMereDe(X, Y).
estParentDe(X, Y) :- estLePereDe(X, Y).
estParentDe(X, Y) :- estLaMereDe(X, Y).
estGrandMereDe(X, Z) :- estLaMereDe(X, Y), estParentDe(Y, Z).
estGrandPereDe(X, Z) :- estLePereDe(X, Y), estParentDe(Y, Z).
ontUnParentCommun(A, B) :- estParentDe(X, A), estParentDe(X, B).
aEteMarieA(X, Y) :- aEteLeMariDe(X, Y).
aEteMarieA(X, Y) :- aEteLeMariDe(Y, X).
homme(X) :- aEteLeMariDe(X, Y).
femme(X) :- aEteLeMariDe(Y, X).
estBeauFrereParAllianceDe(X, Z) :- aEteLeMariDe(X, Y), ontUnParentCommun(Y, Z).
estLePereDe(henri_II, francois_II).
estLePereDe(henri_II, charles_IX).
estLePereDe(henri_II, henri_III).
estLePereDe(henri_II, marguerite_de_Valois).
estLaMereDe(catherine_de_Medicis, francois_II).
estLaMereDe(catherine_de_Medicis, charles_IX).
estLaMereDe(catherine_de_Medicis, henri_III).
estLaMereDe(catherine_de_Medicis, marguerite_de_Valois).
homme(francois_II).
homme(charles_IX).
homme(henri_III).
femme(marguerite_de_Valois).
aEteLeMariDe(henri_IV, marguerite_de_Valois).
1.4 Clauses existentielles
Notre formalise ne permet pas de représenter directement des
propriétés du type ∀ x ∃ y P(x,y). Il existe cependant
une transformation simple, appelée skolémisation, qui permet de
le faire. La propriété ci-dessus est équivalente à l'existence d'une
fonction f telle que ∀ x P(x, f(x)).
2 Résolution propositionnelle
Plaçons d'abord dans le cas où l'on ne fait pas intervenir de
variables ni de termes : les règles de déduction sont alors de simples
implications de la forme P1 ∧ ... ∧ Pn ⇒ P.
Étant donné un tel ensemble de règles, une démonstration d'une
propriété P est un arbre de preuve de la forme :
Chaque règle
se lit : P s'obtient
par application de la règle A sur les hypothèses P1 à Pn.
Pour rechercher un tel arbre de preuve, on peut procéder ainsi :
pour chaque règle , on essaye de
relancer récursivement le procédé pour démontrer
les hypothèses P1 à Pn.
On peut également voir cela de la façon suivante :
on considère le graphe orienté G dont les sommets sont des arbres de
preuve éventuellement incomplets (i.e. on n'a pas démontré toutes les
branches de l'arbres), et dont les arêtes π1 → π2
sont présentes si l'arbre π2 est égal à l'arbre π1 dans
lequel on a remplacé une proposition P0 non démontrée par
l'application d'une règle A de conclusion P0 et d'hypothèses
P1 à Pn : autrement dit, on remplace une sous-branche de la
forme par un sous-arbre de la forme
.
Le problème de savoir s'il existe une démonstration de
P se résume donc à savoir s'il existe un chemin de l'arbre de preuve
incomplet
à un arbre de preuve complet (qui constitue
donc une démonstration de P).
Si l'ensemble des règles applicables est infini, ce graphe peut être
infini. Les méthodes de parcours en profondeur et en largeur peuvent
être utilisées pour trouver une solution : la méthode en profondeur
peut être plus facile à implémenter, mais elle peut partir dans des
branches de raisonnement stérile et ne pas découvrir une
démonstration ; le parcours en largeur doit découvrir toutes les
démonstrations possibles. Notons que dans les deux cas, s'il n'existe
pas de preuve alors l'exploration peut ne pas terminer.
3 Unification
Nous utilisons en fait des règles quantifiées universellement, avec
des termes en argument.
Une règle R de la forme
∀ x1 ... ∀ xn
P1(x1, ..., xn) ∧ ... ∧ Pm(x1, ..., xn)
⇒ P(x1, ..., xn) représente en fait une infinité de
règles sans variables : R dans laquelle on a remplacé
x1,...,xn par des termes quelconques.
Cela justifie notre discussion de la recherche de preuves avec un
nombre infini de règles.
La recherche d'une règle dont la conclusion correspond à la propriété
P choisie est maintenant plus complexe. Par exemple, si l'on a une règle R
de la forme Q(x, y, z) ⇒ P(x, S(y), T(z)) et qu'on cherche
à démontrer ∃ a ∃ b ∃ c P(S(a), b, c), on pourra
appliquer R avec x=S(a), b=S(y), c=T(z) ; on devra donc ensuite démontrer
l'hypothèse Q en tenant compte de ces choix.
Le processus par lequel on rapproche deux termes, ici P(x, S(y),
T(z)) et P(S(a), b, c), en cherchant sous quelles conditions
minimales sur les variables ces termes peuvent être syntaxiquement
égaux s'appelle unification. Formellement parlant, un
unificateur de deux termes t1 et t2 est une substitution
associant un terme (avec variables) à chaque variable ; on note
σ.t le résultat de la substitution dans t selon les règles de
σ. Ce que l'on recherche, c'est un unificateur général, de
telle sorte que tout autre unificateur qui convienne soit un cas
particulier de cet unificateur général, c'est-à-dire qu'il se
décompose en la composée σ1 ∘ σ2 de deux
substitutions.
L'algorithme d'unification est simple. Prenons par exemple l'unification des
deux termes
P(x, S(y), T(z)) et P(S(a), b, c). Les symboles de tête coïncident
(mais on n'aurait pas pu, par exemple, unifier P(x,y) et Q(x,y));
on peut donc continuer. On va unifier x et S(a) ; on met donc à
jour σ en rajoutant la substitution x ↦ S(a). On passe
ensuite à l'unification de S(y) et b ; on obtient alors b ↦
S(y).
Il convient cependant de faire attention au phénomène dit de
capture des variables. Prenons par exemple une règle R :
∀ x P(x) ⇒ Q(x) ; nous cherchons à démontrer
∃ x Q(f(x)). Une approche naïve serait d'unifier Q(x) et
Q(f(x)), et cela nous donne x ↦ f(x), ce qui est bizarre et
même indésirable (voir plus loin). Notons que la règle R est
strictement équivalente à la règle
∀ x' P(x') ⇒ Q(x') par renommage des variables.1
Si on emploie cette règle, on obtient x' ↦ f(x), ce qui est
raisonnable. Il convient donc, avant d'essayer d'appliquer une règle,
de renommer les variables de cette règle en des noms frais (non déjà
utilisés).
Un autre problème est celui du test d'occurrence
(
occur-check). Nous ne désirons pas avoir des solutions comme
x ↦ f(x), c'est-à-dire des solutions où une variable
intervient dans sa propre définition. Prenons un exemple simple pour
voir en quoi ceci est indésirable :
supposons que nous ayons une règle
∀ x P(S(x)) ⇒ P(x), une
formalisation d'une propriété P sur les entiers naturels telle que
∀ n ∈  P(n+1) ⇒ P(n). Une solution de la
forme x = S(x) donnerait n=n+1, une solution absurde. En fait, si
notre seule hypothèse est ∀ n ∈
P(n+1) ⇒ P(n). Une solution de la
forme x = S(x) donnerait n=n+1, une solution absurde. En fait, si
notre seule hypothèse est ∀ n ∈ 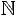 P(n+1) ⇒
P(n), nous ne pouvons pas démontrer P(0). En conséquence, il devra
y avoir un test pour que la définition d'une variable dans une
substitution ne fasse pas intervenir cette même variable.
P(n+1) ⇒
P(n), nous ne pouvons pas démontrer P(0). En conséquence, il devra
y avoir un test pour que la définition d'une variable dans une
substitution ne fasse pas intervenir cette même variable.
4 Syntaxe et utilisation
Nous avons proposé ci-dessus des exemples écrits dans une syntaxe
proche de celle du langage Prolog. Ces exemples sont une succession de
trois types de commandes :
-
des règles de la forme P :- P1, P2,...,Pn.,
représentant
∀ x1 ... ∀ xn P1 ∧ ... Pn ⇒ P ;
on distingue les variables des constantes par le fait que les
variables prennent une majuscule initiale, tandis que les constantes
n'en prennent pas ;
- des axiomes de la forme P. ; il s'agit juste
d'une commodité de notation pour P :- . ;
- des requêtes de la forme ?- P.
En réponse à une requête P :
-
s'il n'y a pas de variable dans la requête P, le système
cherche au moins une preuve de P ; s'il en trouve une, il affiche
yes ; s'il n'en trouve pas, il affiche no ; il
peut très bien ne pas terminer s'il n'existe pas de preuve (ou si sa
recherche est trop longue) ;
- s'il y a au moins une variable, le système va afficher
l'ensemble des solutions trouvées.
Ainsi, sur l'exemple familial ci-dessus, la requête
?- estBeauFrereParAllianceDe(henri_IV, X).
va produire les solutions :
{
X -> francois_II()
}
{
X -> charles_IX()
}
{
X -> henri_III()
}
{
X -> marguerite_de_Valois()
}
Remarquons qu'il y a une faiblesse dans la définition de frère et
soeur : une personne est considérée comme son propre frère (ou sa
propre soeur).
L'ajout et l'utilisation d'une propriété different et
d'axiomes different(x, y) pour toute paire de personnes
différentes est laissé comme exercice au lecteur.
Il n'est pas demandé de faire un algorithme optimisé. Il existe
cependant un grand nombre d'optimisations possibles : simplification
des unificateurs ; si pour démontrer une propriété P, on demande de
démontrer la même propriété ou une propriété essentiellement
isomorphe, alors on arrête dans cette voie ; etc.
Remarquons que certaines règles peuvent provoquer de tels problèmes :
il s'agit notamment des règles d'associativité et de commutativité.
- 1
- On appelle parfois ce renommage α-conversion.
Ce document a été traduit de LATEX par HEVEA
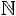 ,+) des entiers naturels)
s'exprime par les axiomes :
,+) des entiers naturels)
s'exprime par les axiomes :
 P(n+1) ⇒ P(n). Une solution de la
forme x = S(x) donnerait n=n+1, une solution absurde. En fait, si
notre seule hypothèse est ∀ n ∈
P(n+1) ⇒ P(n). Une solution de la
forme x = S(x) donnerait n=n+1, une solution absurde. En fait, si
notre seule hypothèse est ∀ n ∈ 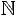 P(n+1) ⇒
P(n), nous ne pouvons pas démontrer P(0). En conséquence, il devra
y avoir un test pour que la définition d'une variable dans une
substitution ne fasse pas intervenir cette même variable.
P(n+1) ⇒
P(n), nous ne pouvons pas démontrer P(0). En conséquence, il devra
y avoir un test pour que la définition d'une variable dans une
substitution ne fasse pas intervenir cette même variable.