Calculs de relations entre constantes numériques par
l'algorithme « LLL »
Sujet proposé par Frédéric Chyzak
(*)
frederic.chyzak[at]inria.fr |
1 Objectif
Il s'agit pour ce sujet d'implanter un algorithme de réduction de
réseau, connu sous le nom de « LLL », d'après le nom de ses
inventeurs, A. K. Lenstra, H. W. Lenstra et L. Lovász. Parmi les
applications possibles de cet algorithme, on notera :
- la factorisation de polynômes d'une variable en temps polynomial ;
- le cassage d'un cryptosystème (maintenant abandonné
;-) )
basé sur le problème du sac à dos ;
- la mise en évidence de la faiblesse de toute une classe de
générateurs de nombres (pseudo-)aléatoires ;
- la recherche de relations de dépendance linéaire à coefficients
entiers entre plusieurs nombres réels donnés par des approximations
numériques ;
- la détermination du polynôme minimal d'un nombre algébrique
donné par une approximation numérique.
On s'intéressera particulièrement dans ce sujet aux deux dernières
applications ; la première est très importante par ses conséquences
mais demanderait un trop gros effort de programmation.
1.1 Dépendances linéaires entres constantes numériques
Étant donnés n nombres réels non nuls, r1, ..., rn, une
relation de dépendance linéaire à coefficients entiers entre ces réels
est une relation de la forme
c1r1+...+cnrn=0
pour des coefficients ci entiers non tous nuls. Lorsqu'on se donne
une approximation rationnelle de chaque réel ri, ou mieux, la
possibilité d'obtenir autant de chiffres décimaux que souhaité, une
approche possible pour la détermination de relations de dépendance
linéaire est de rechercher un vecteur « court », c'est-à-dire de
norme petite en un sens à préciser, parmi les combinaisons linéaires à
coefficients entiers des vecteurs lignes de la matrice
| F= |
⎡
⎢
⎢
⎢
⎢
⎣ |
| 1 |
0 |
... |
0 |
a1 |
| 0 |
1 |
... |
0 |
a2 |
| |
|
⋰ |
|
⋮ |
| 0 |
... |
0 |
1 |
an−1 |
| 0 |
... |
0 |
0 |
an |
|
⎤
⎥
⎥
⎥
⎥
⎦ |
, |
Un vecteur court est alors de la forme
v=(c1,...,cn−1,c1a1+...+cnan)
≃
(c1,...,cn−1,N(c1r1+...+cnrn)).
En particulier,
|
|c1r1+...+cnrn|
≃
|
| |
N−1(c1a1+...+cnan) |
| |
≤ N−1|v|
|
c1r1+...+cnrn=0
un bon candidat pour une relation de dépendance entre les ri. Bien
qu'un tel argument ne constitue pas une preuve, la preuve formelle de
relation entre constantes a dans un bon nombre de cas été grandement
facilitée une fois que la bonne relation a pu être découverte
expérimentalement par la méthode proposée ci-dessus. Dans un certain
nombre de cas, même, des identités n'ont pu être prouvées que parce
qu'elles avaient été découvertes heuristiquement en utilisant
l'algorithme LLL.
Donnons un exemple. Des arguments théoriques donnent la certitude que
le nombre
peut se représenter comme l'évaluation en π d'une fonction
polynomiale à coefficients rationnels. Il s'agit donc de trouver une
dépendance linéaire entre
V,1,π,...,πd
pour un degré de polynôme d à déterminer. À peu près tout système
de calcul formel généraliste connait des approximations pour π et
permet de calculer aisément une approximation numérique de V. On
prend donc par exemple a1=N=1025,
a2=31415926535897932384626434≃ Nπ, ...,
a9=94885310160705740071285755038≃ Nπ8,
a10=−166994737192290704961872433≃ NV pour construire la
matrice F. Les normes des vecteurs lignes de cette matrice sont
toutes supérieures à N=1025. Par l'algorithme LLL, on trouve une
base du même réseau de vecteurs, dont le premier vecteur ligne,
v=(c1,...,cn−1,c1a1+...+cnan)=(0,0,120,0,140,0,−15,0,0,33),
est de norme inférieure à 200, tous les autres vecteurs de base étant
de norme supérieure à 400. Les ai étant connus, on trouve
(c1,...,cn)=(0,0,120,0,140,0,−15,0,0,24),
d'où la relation linéaire
qui résout le problème posé.
1.2 Polynôme minimal de nombres algébriques
Un nombre complexe α est dit algébrique (sur les nombres
rationnels) s'il est solution d'un polynôme P à coefficients
rationnels
P(α)=p0+...+pdαd=0.
Pour pouvoir utiliser l'approche de la section précédente, on se
limite au cas de nombres réels.
Étant donnée une approximation numérique (réelle) d'un nombre α
qu'on a de bonnes raisons de penser être algébrique, la détermination
heuristique de P peut se voir comme la recherche d'une relation de
dépendance linéaire sur des approximations numériques rationnelles de
1,α,...,αd.
Dès lors qu'on a une borne supérieure sur le degré d de P, on peut
donc employer la méthode de la section précédente.
Par exemple, soit à déterminer si un nombre
r≃0.26625264629019611453024776557584454817650128610395...
est algébrique. Par la méthode esquissée, en testant jusqu'à d=6 et
pour N=1028, on trouve (à partir de vecteurs lignes de norme
supérieure à 1020), le vecteur court
v=(−1,0,0,54,0,0,−10),
de norme inférieure à 55, tous les autres vecteurs calculés étant de
norme supérieure à 5000. En poursuivant avec la méthode, on trouve
(c1,...,c7)=(−1,0,0,54,0,0,−54),
soit
P=54X6−54X3+1.
En effet, le nombre r s'avère être une approximation du nombre
algébrique
2 Algorithme LLL pour la réduction de base
Étant donnés n vecteurs lignes à entrées rationnelles,
ai=(ai,1,...,ai,n)
pour 1≤ i≤ n, l'algorithme LLL recherche des combinaisons
linéaires
v=c1a1+...+cnan
à coefficients cl entiers tels que les vecteurs lignes v soient
courts, au sens de la norme euclidienne donnée par
|v|2=v12+...+vn2.
L'ensemble des combinaisons linéaires des vecteurs ai est appelé
réseau engendré par les ai. Sous l'hypothèse que les ai soient
linéairement indépendants sur l'anneau 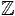 des entiers,
les ai constituent une base du réseau, et l'algorithme LLL calcule
en réalité une base du même réseau constituée exclusivement de
vecteurs courts.
des entiers,
les ai constituent une base du réseau, et l'algorithme LLL calcule
en réalité une base du même réseau constituée exclusivement de
vecteurs courts.
La stratégie adoptée par l'algorithme est de construire la base
courte F en en maintenant en permanence une variante
orthogonale F∗ obtenue par le procédé d'orthogonalisation de
Gram–Schmidt.
2.1 Orthogonalisation par la méthode de Gram–Schmidt
On dote l'espace 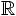 n du produit scalaire scalaire euclidien
donné par
n du produit scalaire scalaire euclidien
donné par
(u∣ v)=u1v1+...+unvn
et de la norme euclidienne donnée par
Étant donnée une base quelconque F=(f1,...,fn) de 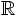 n,
le procédé de Gram–Schmidt calcule une base orthogonale en calculant
successivement, pour i de 1 à n
n,
le procédé de Gram–Schmidt calcule une base orthogonale en calculant
successivement, pour i de 1 à n
|
fi∗=fi− |
|
μi,jfj∗
où
μi,j= |
|
.
|
2.2 Réduction de base
Le coeur de l'algorithme LLL est le suivant : étant donnée une base
F=(f1,...,fn) d'un réseau de 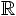 n,
n,
- calculer l'orthogonalisation de Gram–Schmidt de F ;
- en partant de i=2 et tant que i≤ n, faire :
- pour j décroissant de i−1 à 1 remplacer fi par
fi−⌊μi,j+1/2⌋ fj et mettre à jour
l'orthogonalisation de Gram–Schmidt de F ;
- si i≠1 et |fi−1∗|2>2|fi∗|2, échanger fi
et fi−1 et mettre à jour l'orthogonalisation de
Gram–Schmidt de F, puis faire i=i−1 ; sinon faire i=i+1 ;
- renvoyer (f1,...,fn).
(⌊ x⌋ représente le plus grand entier inférieur ou égal
à x, si bien que ⌊ x+1/2⌋ représente l'entier le plus
proche de x.)
3 Considérations théoriques
On montre que si A=max|fi|, l'algorithme LLL effectue O(n4ln
A) opérations arithmétiques sur des entiers de taille O(nlnA).
On pourra s'apercevoir que, même sur des exemples simples tels ceux
donnés dans la section d'exemples, des entiers de plus de 64 bits (les
long de Java) seront nécessaires. C'est pourquoi des entiers
en précision arbitraire devront être utilisés. Leur l'implantation
n'est pas demandée : elle justifierait bien plus qu'un projet à elle
seule. Mais fort heureusement la classe java.math.BigInteger
de Java fournit l'accès à de grands entiers.
4 Travail demandé
Le travail minimum demandé est le suivant :
- Programmer les opérations nécessaires sur les nombres rationnels
en définissant une représentation de nombres rationnels à partir
d'entiers en précision arbitraire. En Java, il conviendra d'utiliser
la classe
java.math.BigInteger qui fournit de tels entiers.
(La documentation est disponible sur les pages WEB de l'X.)
- Implanter le procédé d'orthogonalisation de Gram–Schmidt.
- Implanter l'algorithme LLL et le tester sur les exemples de la
section qui suit. On cherchera à comprendre quelle est la précision
des entrées nécessaire pour obtenir un résultat crédible.
5 Autres exemples
Voici quelques autres exemples pour vous permettre de mettre au point
votre programme. (Tous ces exemples sont tirés du livre Modern
Computer Algebra, cité en référence.)
Un tout petit exemple est donné par les vecteurs (12,2) et (13,4),
dont le réseau engendré contient (1,2) et (11,0).
Dans des exemples de l'application à la factorisation de polynômes, on
doit montrer que le réseau engendré par (1,−5136,0), (0,1,−5136)
et (0,0,15625) contient le vecteur (3,1,1), ou que le réseau
engendré par (1,−34967,0), (0,1,−34967) et (0,0,117649) contient
le vecteur (1,1,1).
Une autre application, liée au cassage du cryptosystème mentionné dans
l'introduction, demande de déterminer si l'entier 1215 peut
s'exprimer comme somme (éventuellement avec répétition, mais un petit
nombre de répétitions) des entiers 366, 385, 392, 401, 422 et 437.
Par l'algorithme naïf, on doit tester un nombre exponentiel de
sommes ; par un algorithme de réduction de réseau, on se ramène à une
complexité polynomiale.
Bien d'autres exemples sont donnés sur le site donné en référence.
6 Références
(Me contacter si ces références sont difficiles à trouver.)
- Description originale de l'algorithme : Factoring Polynomials
with Rational Coefficients, Mathematische Annalen 261, pages
515–534, de A. K. Lenstra, H. W. Lenstra et L. Lovász (1982).
- Les chapitres 16 et 17 du livre Modern Computer
Algebra, de Joachim von zur Gathen et Jürgen Gerhard, Cambridge
University Press (1999). Voir aussi l'URL
http://www-math.uni-paderborn.de/mca/.
- Un site entier est dédié à la recherche de relations entre
constantes numériques à l'URL
http://www.cecm.sfu.ca/projects/IntegerRelations/.
This document was translated from LATEX by
HEVEA.
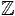 des entiers,
les ai constituent une base du réseau, et l'algorithme LLL calcule
en réalité une base du même réseau constituée exclusivement de
vecteurs courts.
des entiers,
les ai constituent une base du réseau, et l'algorithme LLL calcule
en réalité une base du même réseau constituée exclusivement de
vecteurs courts.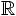 n du produit scalaire scalaire euclidien
donné par
n du produit scalaire scalaire euclidien
donné par
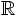 n,
le procédé de Gram–Schmidt calcule une base orthogonale en calculant
successivement, pour i de 1 à n
n,
le procédé de Gram–Schmidt calcule une base orthogonale en calculant
successivement, pour i de 1 à n
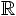 n,
n,