Exploration

Exploration

S ouvent, on recherche un ensemble d'éléments satisfaisant une certaine contrainte parmi un ensemble fini donné. Par exemple, on cherche parmi les sommets d'un graphe les sommets figurant sur un chemin reliant deux sommets donnés, ou on cherche parmi tous les mouvements possibles d'un cavalier sur un échiquier ceux qui permettent de parcourir tout l'échiquier à partir d'une position donneé, ou on cherche parmi tous les pavages possibles ceux qui sont légaux avec des dominos de Wang (carrés à bord colorés dont les couleurs de bords adjacents doivent coïncider) ou avec des polyminos (pentaminos, hexaminos, etc) donnés. Parfois, on complique le problème en introduisant une notion de coût, certaines solutions étant meilleures que d'autres, et on recherche alors la solution de meilleur coût. D'un point de vue abstrait, on peut énoncer le problème sous la forme suivante:

Soit E un ensemble fini. A chaque élément e de E, on affecte une valeur v(e) (en général, un entier positif), on se donne de plus un prédicat (une fonction à valeurs booléennes) C sur l'ensemble des parties de E. Le problème consiste à construire un sous ensemble F de E tel que:
C(F) est satisfait
å_{e Î F}v(e) est maximal (ou minimal, dans certains cas)

Les méthodes développées pour résoudre ces problèmes sont de natures très diverses. Certaines font intervenir la spécificité du problème (par exemple la théorie des graphes pour trouver des chemins reliant deux sommets donnés dans un graphe). Ici nous ne considérerons que des méthodes générales, consistant à explorer tous les sous-ensembles de E, parfois avec des heuristiques particulières. Nous les rangerons en trois catégories: les méthodes gloutonnes, la programmation dynamique et les techniques d'exploration en force brute, encore appelée exploration arborescente (ou backtracking en anglais). L''exploration peut aussi être considérée comme un cas particulier de l'optimisation, quand la notion de coût intervient. Alors on est souvent face à un problème très célèbre et très étudié de l'informatique: la NP-complétude, que nous ne ferons qu'aborder dans ce chapitre.

4.1

Algorithmes gloutons

La technique gloutonne est une des plus rapides méthodes d'exploration. Elle consiste à choisir la solution parmi l'espace de celles possibles en fonction de critères purement locaux, sans besoin d'aucun retour en arrière (backtracking). Cela ne produit pas toujours la solution optimale. Mais, dans les trois cas considérés dans cette section, cela fonctionne très bien.

4.1.1

Affectation d'une ressource

Le problème décrit précisément ci-dessous peut être résolu par l'algorithme glouton (mais, comme on le verra, l'algorithme glouton ne donne pas la solution optimale pour une autre formulation du problème, pourtant proche de celle-ci). Il s'agit d'affecter une ressource unique, non partageable, successivement à un certain nombre d'utilisateurs qui en font la demande en précisant la période exacte pendant laquelle ils souhaitent en disposer.

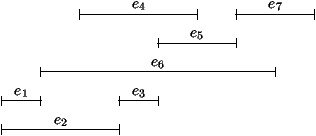
Figure 4.1 : Un planning de réservation pour les locations d'une voiture

On peut matérialiser ceci en prenant pour illustration la location d'une seule voiture. Des clients formulent un ensemble de demandes de location et, pour chaque demande, sont donnés le jour du début de la location et le jour de restitution du véhicule. Le but est d'affecter le véhicule de façon à satisfaire le maximum de clients (et non pas de maximiser la somme des durées de location). On peut formuler ce problème en utilisant le cadre général considéré plus haut. L'ensemble E est celui des demandes de location, pour chaque élément e de E, on note d(e) et f(e) les dates de début et de fin de location (d(e) < f(e)). La valeur v(e) de tout élément e de E est égale à 1 et la contrainte à respecter pour le sous-ensemble F à construire est la suivante:

" e₁,e₂ Î F d(e₁) £ d(e₂) Þ f(e₁) £ d(e₂)

puisque, disposant d'un seul véhicule, on ne peut le louer qu'à un seul client à la fois. Sur la figure 4.1, la solution optimale consiste à prendre les locations e₁, e₃, e₅, e₇. L'algorithme glouton suivant résoud ce problème:

Etape 1: Trier les éléments de E par ordre des dates de fins. Les éléments de E forment une suite á e₁, e₂, ... e_n ñ telle que f(e₁) £ f(e₂), ... £ f(e_n).

Etape 2: Initialiser F = Ø.

Etape 3: Pour i variant de 1 à n, ajouter la demande e_i à F si celle-ci ne chevauche pas la dernière demande appartenant à F.

Montrons que l'on obtient bien ainsi une solution optimale. Soit F = {x₁, x₂, ... x_p} la solution obtenue par l'algorithme glouton et soit G = {y₁, y₂, ... y_q} (q £ p) une solution optimale. Dans les deux cas, nous supposons que les demandes sont classées par dates de fins croissantes. Montrons que p=q. Prenons le premier x_k différent de y_k, c'est-à-dire x_i = y_i pour 1 £ i < k et x_k ¹ y_k. Alors, par construction de F, on a f(x_k) £ f(y_k). Et, on peut remplacer G par G' = {y₁, y₂, ... y_k-1, x_k,y_k+1, ... y_q} tout en satisfaisant à la contrainte de non chevauchement des demandes. Ainsi G', de même cardinalité que G, est aussi une solution optimale, ayant plus d'éléments en commun avec F que n'en avait G. En répétant cette opération, on trouve un ensemble H optimal qui contient F. Comme H est optimal, on a H = F, et donc p=q.

Le programme correspondant est donné ci-dessous. Les tableaux d et f sont donnés en arguments de la fonction location. Pour chaque indice i, ils produisent les dates d(e_i) et f(e_i). On supposera que f est déjà trié en ordre croissant. Le résultat est un tableau de booléens indiquant pour tout i si e_i fait partie de la solution optimale.

static boolean[ ] location (int[ ] d, int[ ] f) { int n = d.length; boolean[ ] r = new boolean[n]; int dernier = -1; for (int i = 0; i < n; ++i) { r[i] = dernier == -1 || f[dernier] <= d[i]; dernier = r[i] ? i : dernier; } return r;}

Si le but est de maximiser la durée totale de location du véhicule, l'algorithme glouton ne donne pas l'optimum. En particulier, il ne considérera pas comme prioritaire une demande de location de durée très importante. L'idée est alors de classer les demandes par durées décroissantes et d'appliquer l'algorithme glouton, malheureusement cette technique ne donne pas non plus le bon résultat (il suffit de considérer une demande de location de 3 jours et deux demandes qui ne se chevauchent pas mais qui sont incompatibles avec la première chacune de durée égale à 2 jours). Le problème de la maximisation de cette durée totale est NP-complet, il est illusoire de penser en trouver un algorithme simple et efficace.

Exercice 23 Montrer que, si on dispose de deux voitures à louer, l'algorithme glouton précédent, triant sur les dates de fin, ne donne pas la solution optimale.

4.1.2

La marche du cavalier

Dans le jeu d'échecs, les mouvements du cheval sont un peu bizarres. Un problème classique consiste à parcourir toutes les cases d'un échiquier avec un cheval à partir d'une position initiale donnée sans repasser deux fois par une même case. On peut montrer que c'est toujours possible (sur un échiquier standard de 64 cases). Une technique gloutonne permet d'écrire un programme marchant sur toutes les cases de départ, sauf une.

On démarre sur la position de départ donnée (c2 sur la figure 4.2 marquée par un cheval blanc). A toute étape, on choisit d'aller sur la case où, le coup suivant, on a le moins de coups possibles (un coup n'est possible que s'il ne passe pas par une case déjà rencontrée). Sur la figure, les 9 premiers coups sont montrés sur la partie gauche; la suite de coups est indiquée sur la partie droite, le coup 0 est en c2, le coup 1 en a1, le coup 2 en b3, etc. Au 10ème coup, on choisit d'aller en f8 où moins de coups sont possibles qu'en f6. Dans cette marche du cavalier, le choix du mouvement suivant ne prend en compte que le nombre de coups réalisables pour le coup qui suit immédiatement; c'est donc une technique gloutonne.

Figure 4.2 : Marche du cavalier sur un échiquier

Ceci aboutit au programme suivant. La fonction marche prend en paramètre la position de départ indiquée par ses coordonnées cartésiennes i et j (0 £ i < 8 et 0 £ j < 8). La fonction modifie le tableau m qui donne la suite des mouvements (comme sur la partie droite de la figure 4.2). On suppose ce tableau initialisé à la valeur négative LIBRE. Pour calculer les nombres de coups possibles, on utilise une fonction auxiliaire jouable testant si une position donnée par ses coordonnées cartésiennes est une position libre à l'intérieur de l'échiquier.

final static int LIBRE = -1;final static int[ ] x = {2, 1, -1, -2, -2, -1, 1, 2};final static int[ ] y = {1, 2, 2, 1, -1, -2, -2, -1};static void marche (int[ ][ ] m, int i, int j) { int coup = -1; int i0, j0; do { m[i][j] = ++coup; i0 = i; j0 = j; int min = Integer.MAX_VALUE; for (int d = 0; d < x.length; ++d) { int n = nbDeCoups (m, i0+x[d], j0+y[d]); if (n < min) { i = i0+x[d]; j = j0+y[d]; min = n; } } } while (i != i0 || j != j0);}static boolean jouable (int[ ][ ] m, int i, int j) { return 0 <= i && i < m.length && 0 <= j && j < m[0].length && m[i][j] == LIBRE;}static int nbDeCoups (int[ ][ ] m, int i, int j) { if ( !jouable (m, i, j) ) return Integer.MAX_VALUE; else { int r = 0; for (int d = 0; d < x.length; ++d) if ( jouable (m, i+x[d], j+y[d]) ) ++r; return r; }}

Exercice 24 Montrer que ce programme fonctionne pour les 64 valeurs de la position de départ, sauf une. Trouver la position de départ problématique. Modifier le programme pour qu'il fonctionne aussi avec cette position de départ.

Cet algorithme ne marche plus pour de grands échiquiers (76 × 76). D'autres algorithmes fonctionnent alors par décomposition de l'échiquier en échiquiers plus petits.

4.1.3

Arbre recouvrant de poids minimal

Un exemple classique d'utilisation de l'algorithme glouton est la recherche d'un arbre recouvrant de poids minimal dans un graphe non dirigé. Plusieurs algorithmes existent: Kruskal, Prim; nous considérons le premier. Ce problème se pose dans la construction de réseaux hydrauliques, électriques ou informatiques. Le graphe correspond alors aux plans d'une ville, d'une maison ou d'un système de relais. Il s'agit de relier des maisons, des pièces ou des sites avec un réseau de coût minimal.

Formellement, on se donne un graphe valué G = (X, A, p) non-orienté et connexe. Pour chaque arc a de A, une fonction de valuation à valeur dans les entiers naturels donne son poids p(a). Comme auparavant, nous représentons le graphe non-orienté par un graphe orienté et symétrique (pour tout a Î A, il existe un arc opposé a' dont l'origine est l'extrémité de a et dont l'extrémité est l'origine de a). La paire (a, a') est une arête. Chaque arête a un poids, et donc a et a' ont même poids, c'est-à-dire p(a) = p(a') pour a Î A. On cherche un arbre recouvrant de poids minimal, c'est à dire un arbre dont la somme des poids des arcs est minimale.

On peut facilement formuler le problème dans le cadre général donné en début de chapitre. On prend pour E l'ensemble des arcs du graphe; la condition C à satisfaire par F est de former un graphe connexe; enfin il faut minimiser la somme des poids des éléments de F. Ce problème peut être résolu très efficacement par l'algorithme glouton suivant :

Etape 1: Classer les arcs par ordre de poids croissants. Ils forment alors une suite e₁, e₂, ... e_n telle que p(e₁) £ p(e₂), ... £ p(e_n).

Etape 2: Initialiser F = Ø

Etape 3: Pour i variant de 1 à n, ajouter l'arête e_i à F si celle-ci ne crée pas de circuit avec celles appartenant à F.

On montre que l'algorithme glouton donne l'arbre de poids minimal en utilisant la propriété suivante des arbres recouvrants d'un graphe.

Proposition 1 Soient T et U deux arbres recouvrants distincts d'un graphe G et soit a une arête de U qui n'est pas dans T. Alors il existe une arête b de T telle que U \ { a } È { b } soit aussi un arbre recouvrant de G.

Plus généralement on montre que l'algorithme glouton donne le résultat si et seulement si la propriété suivante est vérifiée par les sous ensembles F de E satisfaisant C:

Proposition 2 Si F et G sont deux ensembles qui satisfont la condition C et si x est un élément qui est dans F et qui n'est pas dans G, alors il existe un élément de G tel que F \ {x} È {y } satisfasse C.

Un exemple d'arbre recouvrant de poids minimal est donné sur la figure 4.3.

Figure 4.3 : Un arbre recouvrant de poids minimum

4.2

Exploration arborescente

De très nombreux problèmes d'optimisation ou de recherche de configurations particulières donnent lieu à un algorithme qui consiste à faire une recherche exhaustive des solutions. Ces algorithmes paraissent simples puisqu'il s'agit de parcourir systématiquement un ensemble de solutions, mais bien que leur principe ne soit pas particulièrement ingénieux, la programmation nécessite un certain soin.

4.2.1

Sac à dos

Soit E un ensemble d'objets e_i ayant chacun un certain poids p(e_i) (p(e_i) Î R⁺). Soit M la charge maximum que l'on peut emporter dans le sac à dos (M Î N). On veut trouver un ensemble d'objets dont la somme des poids soit la plus voisine possible de M tout en lui étant inférieure ou égale. Le problème est ici formulé dans les termes généraux du début du chapitre, la condition C portant sur le poids du sac à ne pas dépasser. Souvent la formulation du problème du sac à dos fait intervenir deux fonctions: le poids et la valeur, ou encore le volume et le poids. Il s'agit alors d'avoir la valeur maximale avec une borne supérieure sur le poids, ou de minimiser le poids avec une borne supérieure sur le volume. Mais notre présentation simplifiée comporte le même degré de difficulté. Il faut toutefois bien faire attention à définir les valeurs des poids comme non entiers, car sinon un algorithme simple de programmation dynamique peut être réalisé (à condition que M ne soit pas trop grand).

Le problème du sac à dos est un exemple typique classique de problème (NP-complet) pour lequel aucun algorithme efficace n'est connu et où il faut explorer toutes les possibilités pour obtenir la meilleure solution.

Notons n le nombre d'éléments de E, le tableau de booléens sac indique pour tout i (0 £ i < n) si l'objet i est dans le sac. On énumère donc toutes les valeurs possibles de sac et on note le meilleur poids total possible ne dépassant pas la borne M. Le flottant meilleur mémorise la plus petite valeur trouvée pour la différence entre la capacité du sac et la somme des poids des objets qui s'y trouvent. Le tableau sacMax garde en mémoire le contenu du sac qui réalise ce minimum. Les arguments de calcul sont l'objet i à partir duquel on doit prendre des décisions, et la capacité u disponible restante.

static float meilleur = Float.MAX_VALUE;static boolean sac = new boolean[n];static boolean sacMax = new boolean[n];static void calcul (int i, float u) { if (i >= n) { if (u < meilleur) { for (int j = 0; j < n; ++j) sacMax[j] = sac[j]; meilleur = u; } } else { if (p[i] <= u) { sac[i] = true; calcul(i + 1, u - p[i]); sac[i] = false; } calcul(i + 1, u); }}

On vérifie sur des exemples que cette fonction donne des résultats assez rapidement pour n £ 20. Pour des valeurs plus grandes le temps mis est bien plus long car il croît comme 2ⁿ.

4.2.2

Les huit reines

Gauss en 1850 a inventé le problème suivant: placer huit reines sur un échiquier sans qu'aucune d'entre elles ne soit en prise par une autre. On peut en fait définir ce problème pour n reines sur un échiquier de taille n × n. Quand on essaie de le résoudre à la main, cela n'a rien d'évident. Deux solutions se trouvent sur la figure 4.4. On peut démontrer qu'il y a toujours une solution pour n > 3. Un algorithme simple pour en trouver au moins une fonctionne par recherche exhaustive en parcourant l'ensemble des configurations possibles. Pour les valeurs successives de i (0 £ i < 8), on place une reine sur la ligne i et sur une colonne j (0 £ i < 8) en vérifiant bien qu'elle n'est pas en prise. Le tableau pos contient les positions des reines sur chaque ligne. Si une reine figure sur la case de coordonnées i et j, on a pos[i] = j. Pour tester si deux reines placées sur les cases i₁,j₁ et i₂, j₂ sont en prise, on regarde si elles sont sur une même ligne (i₁ = i₂), ou sur une même colonne (j₁ = j₂), ou sur une même diagonale (|i₁ - i₂ | = |j₁ -j₂|).

La fonction qui trouve les solutions au problème des n reines est alors la suivante:

static int[ ] pos = new int[8];static void reines (int i, int n) { if (i < n) for (int j = 0; j < n; ++j) if (compatible (i, j)) { pos[i] = j; reines (i+1, n); } else imprimerLaSolution(pos);}static boolean compatible (int i1, int j1) { for (int i2 = 0; i2 < i1; ++i2) { int j2 = pos[i2]; if (i1 == i2 || j1 == j2 || Math.abs (i1 - i2) == Math.abs (j1 - j2)) return false; } return true;}

Figure 4.4 : Huit reines sur un échiquier

La boucle à l'intérieur de la fonction reines parcourt toutes les positions sur la ligne i compatibles avec les reines déjà placées sur les lignes 0, 1, ...i-1. Les appels successifs de reines modifient la valeur de pos. Quand on a parcouru toutes les lignes, on imprime la solution indiquée par les valeurs du tableau pos, et on continue pour chercher les solutions suivantes. La fonction reines affiche donc toutes les solutions possibles. On peut facilement la modifier pour s'arrêter dès que l'on a trouvé une solution. En lançant reines(0, 8), on trouve ainsi toutes les solutions pour un échiquier 8 × 8. Sur un ordinateur classique, cela prend quelques minutes. Avec des langages plus sophistiqués comme GNU-Prolog, on arrive à trouver toutes les solutions pour n=200. En fait, il existe une formule analytique donnant une solution pour tout n (n > 3).

Exercice 25 Trouver le nombre de solutions au problème des huit reines pour un échiquier de taille 8 × 8.

Dans les deux exemples donnés plus haut, toute la difficulté réside dans le parcours de toutes les solutions possibles, sans en oublier et sans revenir plusieurs fois sur la même. On peut noter que l'ensemble de ces solutions peut être vu comme les sommets d'une arborescence qu'il faut parcourir. La différence avec les algorithmes décrits au chapitre 5 est que l'on ne représente pas cette arborescence en totalité en mémoire mais simplement la partie sur laquelle on se trouve.

4.3

Programmation dynamique

La programmation dynamique consiste à tabuler des résultats intermédiaires pour éviter de recalculer un résultat déjà rencontré. En outre, elle est souvent associée à des problèmes d'optimisation, comme l'avait énoncé son promoteur R. Bellman. Pour résoudre un problème avec de la programmation dynamique, souvent on le généralise, et il devient un des résultats intermédiaires nécessaires à son propre calcul. La tabulation permet d'en accélérer son calcul. Par exemple, considérons le cas de la fonction de Fibonacci. Récursivement elle est définie par

int fib (int n) { if (n < 2) return n; else return fib (n-2) + fib (n-1);}

On supprime la duplication des calculs intermédiaires en écrivant:

int fib (int n) { int[ ] tab = new int[n+1]; tab[0] = 0; tab[1] = 1; for (int i = 2; i <= n; ++i) tab[i] = tab[i-2] + tab[i-1]; return t[n];}

Des esprits chagrins remarqueront que deux valeurs entières suffisent plutot que les n valeurs stockés dans le tableau tab, pour gagner 18 cases de la mémoire dans le calcul de fib(20) qui fait déjà peiner notre ordinateur! La grosse différence vient de la vitesse en O(n) au lieu de O(2ⁿ). Le principe de la programmation dynamique est là: les résultats intermédiaires ont été tabulés, en nombre pas trop élevé, mais suffisamment pour obtenir le résultat final. Dans les techniques d'exploration, beaucoup de cas relèvent de la programmation dynamique.

4.3.1

Plus courts chemins dans un graphe

On considère un graphe valué G= (X,A,l) ayant X comme ensemble de sommets et A comme ensemble d'arcs. On se donne une application l de A dans les entiers naturels. La valeur l(a) est la longueur de l'arc a. La longueur d'un chemin est égale à la somme des longueurs des arcs qui le composent. Le problème consiste à déterminer, pour chaque couple (x_i, x_j) de sommets, le plus court chemin, s'il existe, qui joint x_i à x_j.

Nous commençons par trouver les longueurs des plus courts chemins notées d(x_i, x_j); on convient de noter d(x_i, x_j)= ¥ s'il n'existe pas de chemin entre x_i et x_j. La construction effective des chemins sera examinée ensuite. On suppose qu'entre deux sommets il y a au plus un arc. Les algorithmes de recherche de chemins les plus courts reposent sur l'observation suivante:

Proposition 3 Si f est un chemin de longueur minimale joignant x à y et qui passe par z, alors il se décompose en deux chemins de longueur minimale l'un qui joint x à z et l'autre qui joint z à y.

Dans la suite, on suppose les sommets numérotés x₁, x₂, ... x_n et, pour tout k>0 on considère la propriété P_k suivante pour un chemin:

(P_k(f)) Tous les sommets de f, autres que son origine et son extrémité, ont un indice strictement inférieur à k.

On peut remarquer qu'un chemin vérifie P₁ si et seulement s'il se compose d'un unique arc, d'autre part la condition P_n+1 est satisfaite par tous les chemins du graphe. Notons d_k (x_i,x_j) la longueur du plus court chemin qui vérifie P_k et qui a pour origine x_i et pour extrémité x_j. Cette valeur est ¥ si aucun tel chemin n'existe. Ainsi d₁(x_i,x_j)= ¥ s'il n'y a pas d'arc entre x_i et x_j et vaut l(a) si a est cet arc. D'autre part d_n+1 = d. Le lemme suivant permet de calculer les d_k+1 connaissant les d_k (x_i,x_j). On en déduira un algorithme itératif.

Proposition 4 Les relations suivantes sont satisfaites par les d_k:

d_k+1(x_i, x_j) = min(d_k(x_i,x_j), d_k(x_i,x_k) +d_k(x_k,x_j))

Démonstration Soit un chemin de longueur minimale satisfaisant P_k+1, ou bien il ne passe pas par x_k et on a d_k+1(x_i, x_j) = d_k(x_i,x_j) ou bien il passe par x_k et, d'après la remarque préliminaire, il est composé d'un chemin de longueur minimale joignant x_i à x_k et satisfaisant P_k et d'un autre minimal aussi joignant x_k à x_j. (On ne peut passer plus d'une fois par x_k puisque les longueurs sont toutes positives). Il a donc pour longueur: d_k(x_i,x_k) +d_k(x_k,x_j).

L'algorithme suivant pour la recherche du plus court chemin met à jour une matrice d, valant initialement les longueurs des arcs et ¥ (Integer.MAX_VALUE) s'il n'y a pas d'arc entre x_i et x_j. A chaque itération de la boucle externe, on fait croître l'indice k du d_k calculé.

static void distancesMinimales (GrapheMatVal g) { int n = g.d.length; for (k = 0; k < n; ++k) for (i = 0; i < n; ++i) for (j = 1; j < n; ++j) g.d[i][j] = Math.min(g.d[i][j], g.d[i][k] + g.d[k][j]);}

La classe GrapheMatVal ressemble à la classe GrapheMat considérée dans le chapitre sur les graphes pour la représentation avec des matrices d'adjacence. Dans cette nouvelle classe, la matrice est à présent une matrice de distances d = d₁. Dans le programme précédent, on remarque la similitude avec l'algorithme de Warshall pour trouver la fermeture transitive d'un graphe. Sur l'exemple du graphe donné sur la figure 4.5, la matrice de départ d₁ et le résultat final d sont:

d₁=

æ
ç
ç
ç
ç
ç
ç
ç
è

0	1	¥	4	¥	¥	¥
¥	0	3	2	¥	¥	¥
¥	¥	0	¥	2	¥	¥
¥	¥	¥	0	2	¥	6
¥	3	¥	¥	0	1	¥
¥	¥	¥	2	¥	0	1
4	¥	¥	¥	¥	¥	0

ö
÷
÷
÷
÷
÷
÷
÷
ø

d =

æ
ç
ç
ç
ç
ç
ç
ç
è

0	1	4	3	5	6	7
10	0	3	2	4	5	6
8	5	0	5	2	3	4
8	5	8	0	2	3	4
6	3	6	3	0	1	2
5	6	9	2	4	0	1
4	5	8	7	9	10	0

ö
÷
÷
÷
÷
÷
÷
÷
ø

Figure 4.5 : Un graphe aux arcs valués

Pour produire les chemins les plus courts entre les sommets i et j, on utilise une matrice S qui donne pour tout i et j, le sommet qui suit i dans le chemin le plus court de i à j. Au début, la valeur S₁ de cette matrice contient les éléments S₁(i,j) valant j s'il existe un arc de i à j ou si i=j. Sinon ses éléments prennent la valeur indéfinie ^.

Sur l'exemple précédent, on trouve:

S₁ =

æ
ç
ç
ç
ç
ç
ç
ç
è

ö
÷
÷
÷
÷
÷
÷
÷
ø

S =

æ
ç
ç
ç
ç
ç
ç
ç
è

1	2	2	2	2	2	2
4	2	3	4	4	4	4
5	5	3	5	5	5	5
5	5	5	4	5	5	5
6	2	2	6	5	6	6
7	7	7	4	4	6	7
1	1	1	1	1	1	7

ö
÷
÷
÷
÷
÷
÷
÷
ø

Le calcul de la matrice S et donc du chemin le plus court entre deux sommets i et j se font par les fonctions suivantes:

final static int INDEFINI = -1;static int[ ][ ] sommetSuivant (GrapheMatVal g) { int n = g.d.length; int[ ][ ] s = new int[n][n]; for (i = 0; i < n; ++i) for (j = 0; j < n; ++j) s[i][j] = (g.d[i][j] != Integer.MAX_VALUE) ? j : INDEFINI; for (k = 0; k < n; ++k) for (i = 0; i < n; ++i) for (j = 0; j < n; ++j) if (g.d[i][j] > (g.d[i][k] + g.d[k][j]) { g.d[i][j] = g.d[i][k] + g.d[k][j]; s[i][j] = s[i][k]; } return s;}static void plusCourtChemin (GrapheMatVal g, int i, int j) { distancesMinimales (g); int[ ][ ] s = sommetSuivant (g); for (int k = i; k != j; k = s[k][j]) if (k == INDEFINI) throw new Error ("Chemin inexistant"); System.out.print (k + " "); System.out.println (j);}

4.3.2

Sous-séquences communes

Le problème est de retrouver la plus grande sous-séquence commune à deux chaînes de caractères, ou encore à deux mots sur un alphabet. Ce problème se pose, par exemple, dans la commande diff du système Unix, qui affiche les différences ``minimales `` entre deux fichiers. Dans diff, on fait la différence sur les lignes, mais le coeur de la commande utilise un algorithme analogue à celui que nous voyons dans cette section. De même, pour comparer des chaînes d'ADN, on doit aussi retrouver les plus longues séquences communes.

Une séquence (ou un mot) est une suite finie de symboles (ou lettres) pris dans un ensemble fini (ou alphabet). La longueur de la séquence u est notée |u|, et e dénote la séquence vide (de longueur nulle). Une séquence v=b₁b₂··· b_m est une sous-séquence de u=a₁a₂··· a_n s'il existe des entiers i₁,i₂, ...i_m (0 £ i₁ < i₂ <··· i_m£ n) tels que a_{i_k}=b_k (1 £ k £ m). Une séquence w est une sous-séquence commune aux séquences u et v si w est sous-séquence de u et de v. Une sous-séquence commune est maximale si elle est de longueur maximale.

La plus grande sous-séquence commune ssc(u,v) entre deux séquences u et v est la séquence donnée par la définition récursive suivante:

ssc(u, e)

ssc(e, u) = e

ssc(ua, va)

ssc(u,v)a

ssc(ua, vb)

ì
í
î

ssc(ua, v) si |ssc(ua, v)| ³ |ssc(u, vb)|

ssc(u, vb) sinon

Figure 4.6 : Plus longue sous-séquence commune entre bacb et aaac

En effet, soit w une sous-séquence, de longueur maximale, commune à a₁a₂··· a_i-1 et b₁b₂··· b_j-1. Si a_i = b_j, alors wa_i est une sous-séquence commune maximale à a₁a₂··· a_i et b₁b₂··· b_j. Si a_i ¹ b_j, une sous-séquence commune à a₁a₂··· a_i et b₁b₂··· b_j est ou bien commune à a₁a₂··· a_i et b₁b₂··· b_j-1, ou bien commune à a₁a₂··· a_i-1 et b₁b₂··· b_j, en choisissant le cas donnant la sous-séquence de plus grande longueur.

Sur l'exemple de la figure 4.6, cela est illustré dans le cas où u = bacb et v = aaac. Le premier mot est représenté verticalement, le deuxième horizontalement. Pour chaque caractère de l'un (à la position i) et de l'autre (à la position j), on obtient la plus longue sous-séquence commune à a₁a₂··· a_i et b₁b₂··· b_j en suivant les flèches de la table pred. La flèche diagonale correspond à la deuxième ligne des équations vérifiées par ssc; la flèche vers la gauche correspond à la troisième ligne, la flèche vers le haut à la quatrième.

La longueur de la plus grande sous-séquence commune à a₁a₂ ··· a_i et b₁b₂··· b_j est donnée récursivement par:

L(i,j)=

ì
í
î

1 + L(i-1,j-1)	si a_i = b_j
max(L(i,j-1),L(i-1,j))	sinon

On en déduit les fonctions suivantes pour le calcul de la plus longue sous-séquence commune. Le résultat final se fait en remontant le tableau pred à partir de l'extrémité en bas et à droite.

final static int GAUCHE = 1, HAUT = 2, DIAG = 3;static int longueurSSC (String u, String v, int[ ][ ] pred) { int m = u.length(), n = v.length(); int[ ][ ] longueur = new int[m][n]; for (int i = 1; i < m + 1; ++i) for (int j = 1; j < n + 1; ++j) if (u.charAt(i-1) == v.charAt(j-1)) { pred[i][j] = DIAG; longueur[i][j] = 1 + longueur[i-1][j-1]; } else if longueur[i][j-1] > longueur[i-1][j] { pred[i][j] = GAUCHE; longueur[i][j] = longueur[i][j-1]; } else { pred[i][j] = HAUT; longueur[i][j] = longueur[i-1][j]; } return longueur[m][n];}static String ssc (String u, String v) { int m = u.length(), m = v.length(); int[ ][ ] pred = new int[m][n]; int lg = longueurSSC (u, v, pred); StringBuffer r = new StringBuffer(lg); int i = m, j = n; for (int k = lg-1; k >= 0; ) switch (pred[i][j]) { case DIAG: r.setCharAt(k, u.charAt(i-1)); --i; --j; --k; break; case GAUCHE: --j; break; case HAUT: --i; break; } return new String(r);}

4.4

Programmes en OCaml

(* les n reines, voir page ?? *)let nReines n = let pos = Array.make n 0 in let conflit i1 j1 i2 j2 = i1 = i2 || j1 = j2 || abs(i1 - i2) = abs (j1 - j2) in let compatible i j = try for k = 0 to i-1 do if conflit i j k pos.(k) then raise Exit done; true with Exit -> false in let rec reines i = if i >= n then imprimerSolution pos else for j = 0 to n-1 do if compatible i j then begin pos.(i) <- j; reines (i+1); end done in reines 0;;

(* les n reines (suite) *)open Printf;;let imprimerSolution pos = let n = Array.length(pos) in for i = 0 to n-1 do for j = 0 to n-1 do if j = pos.(i) then printf "* " else printf " " done; printf "\n"; done; printf "----------------------\n";;

(* les sous séquences communes *)let longueur_ssc u v = let n = String.length u and m = String.length v in let longueur = Array.make_matrix (n+1) (m+1) 0 and provient = Array.make_matrix (n+1) (m+1) 0 in for i=1 to n do for j=1 to m do if u.[i-1] = v.[j-1] then begin longueur.(i).(j) <- 1 + longueur.(i-1).(j-1); provient.(i).(j) <- 1; end else if longueur.(i).(j-1) > longueur.(i-1).(j) then begin longueur.(i).(j) <- longueur.(i).(j-1); provient.(i).(j) <- 2; end else begin longueur.(i).(j) <- longueur.(i-1).(j); provient.(i).(j) <- 3; end done done; longueur, provient;;let ssc u v = let n = String.length u and m = String.length v in let longueur, provient = longueur_ssc u v in let lg = longueur.(n).(m) in let res = String.create lg and i = ref n and j = ref m and k = ref (lg-1) in while !k >= 0 do match provient.(!i).(!j) with 1 -> res.[!k] <- u.[!i-1]; decr i; decr j; decr k | 2 -> decr j | _ -> decr i done; res;;