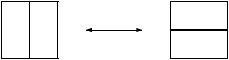Génération de pavages de dominos
Sujet proposé par Daniel Krob
dk@lix.polytechnique.fr
1 Quelques éléments sur les pavages
1.1 Pavages de dominos
Un pavage par des dominos d'un rectangle de taille 2n× m
1
est simplement un recouvrement parfait de ce domaine géométrique par
un ensemble de dominos, c'est-à-dire de rectangles de taille 2× 1
ou 1 × 2. La figure 1 donne un exemple de pavage d'un rectangle
4 × 4 par des dominos.
Figure 1. Un exemple de pavage d'un rectangle 4× 4 par des dominos.
On peut bien entendu considérer bien d'autres types de pavages : pavages par
des dominos de domaines plus complexes que des rectangles, pavages de domaines
par des losanges, etc. Nous renvoyons à [2] pour d'informations sur
ces sujets.
1.2 Fonctions de hauteur
Un outil fondamental pour étudier les pavages de dominos est la fonction
de hauteur d'un pavage. Pour définir cette notion, nous aurons besoin de
choisir au préalable un coloriage régulier alterné (en blanc et en noir)
des différents carrés du plan discret, i.e. 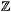 ×
× 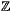 . Pour nous fixer
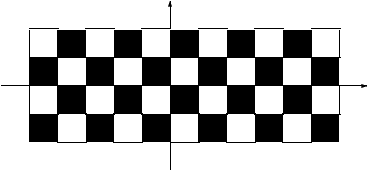
les idées, considérons donc le coloriage qui consiste à colorier en blanc
le carré du plan discret qui contient l'origine et le point de coordonnées
(1,1), puis à alterner carrés blancs et carrés noirs dans toutes les
directions du plan (voir figure 2).
. Pour nous fixer
les idées, considérons donc le coloriage qui consiste à colorier en blanc
le carré du plan discret qui contient l'origine et le point de coordonnées
(1,1), puis à alterner carrés blancs et carrés noirs dans toutes les
directions du plan (voir figure 2).
Figure 2. Le coloriage de référence du plan discret.
La fonction de hauteur d'un pavage d'un rectangle par des dominos
est une fonction qui associe une valeur numérique à chacun des points
du plan discret qui se trouvent à l'intérieur du rectangle que l'on
considère. Pour chaque pavage p d'un rectangle R du plan discret,
cette fonction se définit de la manière suivante :
-
on commence par affecter la valeur 0 au coin du rectangle R qui
se trouve le plus en bas à gauche,
- pour trouver la valeur de la fonction de hauteur de p en un point
p quelconque du plan discret contenu dans R, on utilise la méthode
suivante :
-
on initialise une variable h à 0,
- on prend un chemin c quelconque de l'origine à p qui n'emprunte
que des segments de droite appartenant au pavage p de R,
- on oriente chaque segment élémentaire
2
de c dans le sens obtenu en suivant c pour aller de l'origine
à p,
- on parcourt, segment élémentaire par segment élémentaire, le
chemin c et en ajoutant (resp. soustrayant) 1 à h chaque fois que
l'on a un carré noir (resp. blanc) à la gauche (par rapport à son
orientation courante) du segment courant.
La valeur de h lorsque l'on arrive à p est alors la valeur de la fonction
de hauteur de p en p.
On admettra que la définition que nous venons de donner est bien cohérente,
autrement dit que le choix du chemin c n'a pas d'importance sur le
résultat du calcul de la fonction de hauteur.
La figure 3 qui suit illustre le calcul des fonctions de hauteur de deux pavages
d'un rectangle 2 × 4 en tous les points de ces pavages.
Figure 3. Le calcul des fonctions de hauteur de deux pavages d'un rectangle
2× 4.
La notion de fonction de hauteur donne un test pratique pour vérifier
l'équivalence de deux pavages : on peut en effet montrer que deux
pavages d'un même rectangle sont identiques si et seulement si leurs
fonctions de hauteur sont égales en tout point du plan discret contenu
dans le rectangle.
1.3 Ordre sur les pavages
La notion de fonction de hauteur permet de mettre un ordre (partiel) sur les
pavages d'un même rectangle R du plan discret. On dira en effet qu'un
pavage p est plus petit qu'un pavage p' de R lorsque la valeur
de la fonction de hauteur de p est inférieure ou égale à la valeur de
la fonction de hauteur de p' en tout point du plan discret contenu dans
le rectangle R.
Le premier pavage de la figure 3 est ainsi plus petit que le deuxième pavage
de cette même figure au sens de l'ordre partiel que nous venons ainsi de
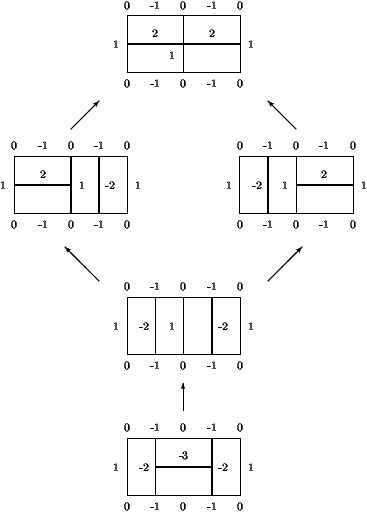
définir. Le lecteur pourra de même vérifier que la figure 4 qui suit
donne la structure de l'ordre que nous venons de définir sur l'ensemble
des pavages du rectangle 2 × 4. On remarquera tout particulièrement
sur cette figure que le troisième et le quatrième pavage (en partant
du bas) sont deux à deux non comparables au sens de l'ordre que nous
venons de définir.
L'ordre que nous venons ainsi de définir permet en fait de mettre une
structure de treillis sur l'ensemble de tous les pavages d'un même rectangle
R. Deux pavages quelconques p et p' de R admettent en effet
toujours une borne inférieure µ = min(p,p'), i.e. un
pavage µ de R qui est inférieur ou égal (au sens de notre ordre)
à la fois à p et à p' et tel que tout pavage de R inférieur
ou égal à la fois à p et p' est aussi inférieur ou égal à
µ. On admettra que cette borne inférieure est un pavage de R qui est
caractérisé par le fait que la valeur de sa fonction de hauteur est
en tout point égale au minimum des valeurs des fonctions de hauteur des
pavages p et p' prises en ce point. On peut aussi montrer que tout
couple de pavages de R admet de même une borne supérieure qui est
caractérisée de manière tout à fait similaire
3 .
Les propriétés des pavages d'un rectangle que nous venons
de rappeler impliquent en particulier qu'il existe toujours un unique
pavage minimal (resp. maximal) de ce rectangle, i.e. qui est inférieur
(resp. supérieur) ou égal à tout pavage du rectangle considéré.
On appelera donc ce pavage le pavage minimal (resp. maximal) du
rectangle. Nous laissons au lecteur le soin de trouver une construction
et une caractérisation de ces deux pavages pour un rectangle donné.
Figure 4. Les 5 pavages (ordonnés) du rectangle 2× 4.
1.4 Hauteur d'un pavage
L'ordre que nous venons de définir sur les pavages d'un rectangle
R possède une propriété géométrique remarquable. On peut en effet
montrer que l'on peut toujours passer d'un pavage p à l'un des pavages
p' de R qui est son successeur immédiat dans l'ordre précédent,
en effectuant (dans l'un des deux sens possibles) l'opération géométrique
suivante -- appelée un flip -- sur l'une des paires de deux dominos
qui remplissent un carré 2× 2 au sein du pavage p.
Figure 5. Les deux flips possibles sur une partie d'un pavage.
Le lecteur pourra de fait vérifier sur la figure 4 que l'on passe bien
toujours d'un pavage p du rectangle 2× 4 à l'un de ses successeurs
immédiats par une opération de flip appliquée à une partie du pavage
p que l'on considère initialement.
On peut maintenant facilement définir la notion de hauteur d'un
pavage d'un rectangle R comme le nombre minimal de flips nécessaires
à son obtention en partant du pavage minimal de R. La figure 4 peut donc
aussi être vu comme une représentation de l'ensemble de tous les pavages
du rectangle 2× 4, classés par ordre de hauteur croissant
4 .
2 Travail demandé
On demande d'écrire un programme qui génère et qui affiche tous les
pavages d'un rectangle donné. La méthodologie à utiliser sera la
suivante :
-
Construction du pavage minimal : on proposera à cet effet un
algorithme récursif dédié à cette construction.
- Génération de l'ensemble (ordonné) des pavages par hauteurs
successives : on partira du pavage minimal
5
et on appliquera tous les flips possibles à l'ensemble des pavages
d'une hauteur donnée déjà construits
6 .
- Affichage des pavages obtenus : l'affichage devra être
effectué sous la forme de la figure 4. Attention néanmoins à
prendre en considération le fait que le nombre de pavages d'un
rectangle peut être élevé -- même pour de petits rectangles --
ce qui nécessite de mettre en place une technique de fenêtre
glissante pour gérer l'affichage.
On pourra également prévoir des possibilités d'impression des
figures obtenues.
3 Extensions possibles
De très nombreuses extensions du sujet existent. Nous en citons ci-dessus
quelques unes à titre d'exemple.
-
Amélioration de l'algorithme de génération proposé :
l'algorithme proposé possède un inconvénient car il nécessite de
tester tous les flips possibles et de générer souvent plusieurs pavages
identiques à partir d'un pavage donné, ce qui ralentit son efficacité.
On pourra donc proposer des méthodes qui permettent d'éviter ce type de
problèmes.
- Prise en compte de domaines plus complexes à paver comme les
diagrammes de Ferrers ou les polyominos généraux : les propriétés des
pavages que nous avons présentées sont en fait les mêmes lorsque l'on
considère un domaine quelconque du plan pavable par des dominos. On
pourra donc implémenter un algorithme de génération de tous les
pavages d'un diagramme de Ferrers ou d'un polyomino pavable par des dominos
(voir [1] pour les définitions de ces deux notions)
7 .
- Prise en compte d'autres types de pavages comme les pavages du
plan par des losanges : les propriétés des pavages que nous avons
présentées sont en fait les mêmes lorsque l'on considère un domaine
quelconque du plan pavable par des losanges (voir [2]). On pourra
donc implémenter un algorithme de génération de tous les pavages
d'un domaine régulier du plan pavable par des losanges.
- Génération aléatoire de pavages : (difficile) on pourra
utiliser les idées présentées dans ce sujet pour proposer et implémenter
un algorithme capable d'engendrer aléatoirement des pavages d'un domaine
donné avec probabilité uniforme (par rapport à tous les pavages
de ce domaine).
Références
-
[1]
- Krob D., Eléments de combinatoire, Rapport
interne LITP 95/54, Novembre 1995
8
- [2]
- Thurston W.P., Conway's tiling groups, Amer. Math.
Monthly, 97, 8, 757-773, 1990
- 1
- Les rectangles dont les deux cotés sont de longueur
impaire sont trivialement non pavables par des dominos.
- 2
- Un segment élémentaire est un segment horizontal ou vertical
de longueur 1.
- 3
- On rappelle que le fait que l'ensemble des pavages d'un
rectangle est un treillis signifie juste que tout couple de pavages
de ce rectangle admet à la fois une borne inférieure et
supérieure.
- 4
- Dans ce cas, il y a 1 pavage de hauteur 0, 1 pavage de
hauteur 1, 2 pavages de hauteur 2 et 1 pavage de hauteur 3
- 5
- Qui est par définition le seul pavage de hauteur 0.
- 6
- Comme des flips différents appliqués à des pavages
différents peuvent conduire au même pavage (cf figure 4), il
est nécessaire de prévoir une procédure spécifique de test
de l'équivalence de deux pavages (voir paragraphe
1.2).
- 7
- Dans ce cas, il sera nécessaire de mettre en place au
préalable une procédure permettant de tester si un tel domaine
plus étendu est bien pavable par des dominos (cf [2]).
- 8
- Voir la rubrique Rapports internes du site
http:\\www.liafa.jussieu.fr
Ce document a été traduit de LATEX par
HEVEA.


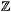 ×
× 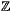 . Pour nous fixer
les idées, considérons donc le coloriage qui consiste à colorier en blanc
le carré du plan discret qui contient l'origine et le point de coordonnées
(1,1), puis à alterner carrés blancs et carrés noirs dans toutes les
directions du plan (voir figure 2).
. Pour nous fixer
les idées, considérons donc le coloriage qui consiste à colorier en blanc
le carré du plan discret qui contient l'origine et le point de coordonnées
(1,1), puis à alterner carrés blancs et carrés noirs dans toutes les
directions du plan (voir figure 2).