Le problème de Post
Projet proposé par Gilles Dowek1
Prélude
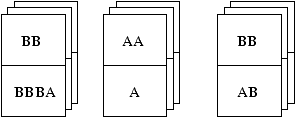
On considère un jeu de dominos. Sur chacun des dominos se trouvent
inscrits deux mots (un en haut et un en bas). Ces dominos sont de trois
types : sur les dominos du premier type sont inscrits les mots BB et
BBBA, sur ceux du deuxième type sont inscrits les mots AA et A, sur ceux
du troisième type les mots BB et AB. Il y a une infinité de dominos de
chaque type.
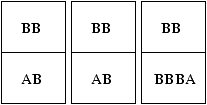
Si on assemble deux dominos du troisième type, puis un domino du
premier type
on forme les mots BBBBBB et ABABBBBA qui sont différents.
Pour ouvrir la porte magique, il faut trouver un
assemblage non vide de dominos, tel que les deux mots formés soient
identiques. Est-ce possible ?
Le problème de Post
Une instance E du problème de Post est un ensemble fini de types de
dominos, c'est-à-dire une partie finie de
{A,B}* 2.
Une solution d'une telle instance E est une suite finie non vide de
dominos de E qui forme deux mots identiques, c'est-à-dire une
suite finie d'éléments de E telle que le mot obtenu en concaténant
parties gauches des couples de cette suite soit identique à celui
obtenus en concaténant leurs parties droites.
Emil Post (1897-1954) a démontré en 1946 que ce problème était
indécidable : on ne peut pas écrire de programme qui indique si
une instance du problème de Post a une solution ou non. En revanche,
on peut écrire un programme qui cherche une solution, en trouve
toujours une si l'instance testée a une solution, mais peut boucler si
ce n'est pas le cas. On appelle un tel programme un programme de
semi-décision.
Un programme de semi-décision
Le projet consiste à écrire un tel programme, puis à l'améliorer.
Soit une instance E du problème de Post, on considère le graphe
infini suivant : ses sommets sont tous les couples de mots et il y a
un arc allant du sommet (m,n) à tous les sommets de la forme
(ma,nb) où (a,b) est un couple de E. Ce graphe est à
branchement fini. L'instance E a une solution s'il y a un chemin
non trivial dans ce graphe allant du sommet (e,e) à un
sommet de succès de la forme (p,p).
Dans un graphe infini le parcours en profondeur d'abord n'est pas
complet, en effet dans l'exemple de la page précédente, il amènerait à
suivre la branche infinie ((BB)n,(BBBA)n) sans
jamais revenir en arrière. En revanche un parcours en largueur
d'abord est complet, dans le sens que chaque sommet accessible depuis
(e,e) sera visité à un certain moment (même s'il est
faux qu'à un certain moment tous ces sommets auront été visités).
Écrire un programme de semi-décision pour le problème de Post en
utilisant en parcours de graphe en largeur d'abord.
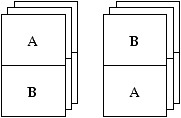
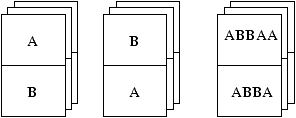
On pourra essayer ce programme avec l'exemple ci-dessus ainsi qu'avec
les exemples suivants.
Élaguer pour échouer
Le programme auquel on a abouti trouve toujours une solution si
l'instance testée en a une, mais il n'échoue jamais. On peut
l'améliorer de manière à ce qu'il échoue dans un certain nombre de cas
où l'instance testée n'a pas de solution (même s'il est impossible
qu'il échoue toujours dans ce cas, puisque le problème est indécidable).
Une première manière de le faire échouer est d'exploiter le fait
que dans un sommet de la forme (m,n) si m n'est pas un préfixe
de n et n n'est pas un préfixe de m, alors le sommet est sans
espoir : aucun sommet accessible depuis ce sommet ne sera un sommet de
succès de la forme (p,p). Par exemple dans tous les sommets
accessibles depuis (A,B) le premier mot commence
par la lettre A et le second par la lettre B. Il n'est donc pas utile
de poursuivre l'exploration à partir d'un tel sommet.
Écrire un programme de semi-décision pour le problème de Post
qui utilise cette amélioration. On pourra l'essayer sur les quatre
instances ci-dessus.
La simplification des équations
Une deuxième amélioration utilise le fait que l'équation
ABBAA x = ABBA y
a les mêmes solutions que l'équation
Ax = y
De ce fait, une suite de dominos mène du sommet
(ABBAA, ABBA) à un sommet de succès si et
seulement si elle mène du sommet (A, e) à un sommet de
succès.
De ce fait, on peut modifier la définition du graphe ci-dessus en
posant un arc allant du sommet (m,n) à tous les sommets de la
forme simple(ma,nb) où (a,b) est un couple de E,
simple(ma,nb) ¹ Fail et simple
est la fonction de {A,B}*2 dans
{A,B}*2 È {Fail}
définie par
simple(e, y) = (e, y)
simple(x, e) = (x, e)
simple(A x, A y) = simple(x, y)
simple(B x, B y) = simple(x, y)
simple(A x, B y) = Fail
simple(B x, A y) = Fail
Écrire un programme de semi-décision pour le problème de Post
qui utilise cette amélioration. On pourra l'essayer sur les quatre
instances ci-dessus.
Travail demandé
Écrire un programme qui prend en argument une liste de couples de mots
et qui recherche une solution de l'instance du problème de Post
définie par cette liste. Le programme utilisera les deux optimisations
ci-dessus de manière à échouer pour certains problèmes qui
n'ont pas de solution.
Est-il possible d'améliorer encore ce programme de manière à ce
qu'il échoue plus souvent ?
- 1
- Gilles.Dowek@polytechnique.fr
Ce document a été traduit de LATEX par
HEVEA.