Arbre de longueur minnimale

Sujet proposé par Olivier Devillers

Olivier.Devillers@sophia.inria.fr Difficulté : moyen (**).

1  Préambule

Étant donné un ensemble de points S dans le plan on cherche à relier ces points (par exemple avec des fils téléphoniques) en minimisant la longueur. On obtient alors un arbre, l'arbre couvrant minimal.

Le calcul de l'arbre couvrant minimal se fait en deux étapes, on détermine d'abord la triangulation de Delaunay, puis on extrait de celle ci l'arbre couvrant minimal.

L'arbre couvrant minimal peut également être utilisé pour obtenir en temps O(n3) une approximation du problème du voyageur de commerce qui est NP-complet.

2  Détail du sujet

2.1  Diagramme de Voronoï et triangulation de Delaunay

Étant donné un ensemble S de points dans le plan, on appelle diagramme de Voronoï de S la subdivision du plan permettant de trouver le point de S le plus proche d'un point de requête q.

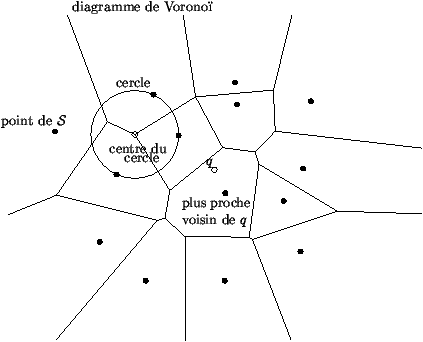
Figure 1 : Diagramme de Voronoï

Clairement, les arêtes d'un tel diagramme sont des portions de médiatrices entre deux points de S, les sommets sont des centres de cercle passant par trois points.

Le dual du diagramme de Voronoï est la triangulation de Delaunay, on l'obtient en reliant les points de S dont les cellules de Voronoï sont voisines. On obtient ainsi une triangulation de S, c'est-à-dire une subdivision de l'enveloppe convexe de S en triangles ayant les points de S pour sommets.

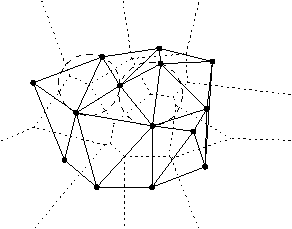
Figure 2 : Triangulation de Delaunay (trait pleins) et diagramme de Voronoï (pointillé)

Un triangle appartient à la triangulation de Delaunay si et seulement si son cercle circonscrit ne contient aucun point de S.

Les triangles de Delaunay correspondent aux sommets de Voronoï, les sommets de Delaunay aux cellules de Voronoï et les arêtes de Delaunay aux arêtes de Voronoï; c'est pourquoi on parle de graphes duaux.

Pour en savoir plus on pourra consulter le livre de J.-D. Boissonnat et M. Yvinec [BY95] ou le poly du cours de majeure "Géométrie et synthèse d'images" (http://www-sop.inria.fr/personnel/devillers/x/).

2.2  Algorithme de calcul de Delaunay

Un premier algorithme simple consiste à calculer la triangulation incrémentalement, c'est-à-dire en ajoutant les points un à un. Supposons que l'on ait calculé la triangulation de Delaunay DTS de S et que l'on cherche à calculer le triangulation de SÈ{p}: On peut donc examiner tous les triangles de DTS pour déterminer ceux dont le cercle circonscrit contient p, ces triangles doivent disparaître. Les nouveaux triangles sont ceux qui ont p comme sommet, on les obtient en reliant p au bord du trou laissé par les triangles détruit.

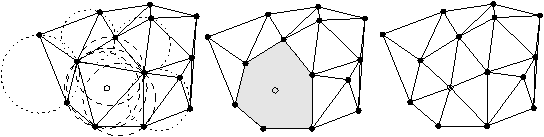
Figure 3 : Insertion d'un point. 1) les triangles à détruire. 2) la zone détruite. 3) la nouvelle triangulation.

Le cas ou le nouveau point p est extérieur à l'enveloppe convexe se traite de manière similaire.

2.3  Localisation par marche dans la triangulation

En faisant les deux remarques suivantes On peut en déduire une amélioration de l'algorithme précédent. Plutôt que d'examiner tous les triangles de DTS pour déterminer les triangles à détruire, on peut chercher le triangle contenant p en marchant dans la triangulation, puis trouver tous les triangles à détruire en utilisant les relations de voisinage entre triangles.

Par marcher dans la triangulation, on veut dire que depuis un triangle connu comme contenant un point o, on va visiter successivement tous les triangles traversés par le segment op et seulement ceux la, on accélère ainsi la phase de recherche des triangles à détruire.

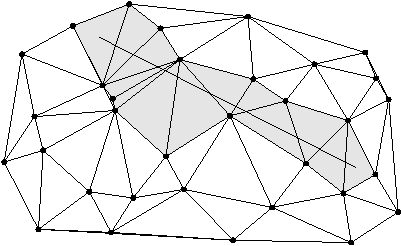
Figure 4 : Triangles visités durant la marche.

2.4  Extraction de l'arbre couvrant minimal

L'extraction de l'arbre couvrant minimal repose sur le théorème suivant

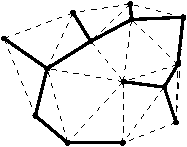
Figure 5 : Arbre couvrant minimal et triangulation de Delaunay.

Théorème :L'arbre couvrant de longueur minimale est inclus dans la triangulation de Delaunay.

La démonstration de ce théorème repose sur ces deux lemmes:

Lemme 1 :si S= S1 È S2 alors la plus courte arête entre un point de S1 et un point de S2 est une arête de la triangulation de Delaunay.

Lemme 2 :si S= S1 È S2 alors la plus courte arête entre un point de S1 et un point de S2 est une arête de l'arbre couvrant minimal.

La démonstration du Lemme 1 repose sur le fait qu'une arête est de Delaunay si et seulement si il existe un cercle passant par ses extrémités en ne contenant pas de points de S (Essayer de faire ces démonstrations).

Ces lemmes nous donne un algorithme facile pour extraire l'arbre de la triangulation de Delaunay.
--- On initialise S1 avec un point pÎ S, S2 avec S\{p} et une queue de priorité avec toutes les arêtes de Delaunay incidente à p.
--- Tant que S2 n'est pas vide
   --- prendre la plus courte arête pq de la queue (pÎ S1 et qÎ S2).    --- enlever q de S2 et l'ajouter à S1    --- enlever de la queue les arêtes contenant q    --- ajouter dans la queue les arêtes allant de q vers un point de S2.

3  Pour aller plus loin

3.1  Le voyageur de commerce

Le problème dit du voyageur de commerce consiste à relier les points entre eux pour former non plus un arbre, mais un circuit de longueur minimale. Ce problème est bien connu pour être NP-complet.

En choisissant un noeud comme racine et parcourant l'arbre couvrant minimal en énumérant les noeuds interne à la descente comme à la montée, on reviens à la racine et on obtient donc un circuit, ce circuit est une 2-approximation du voyageur de commerce (au pire 2 fois trop long).

Il est possible d'obtenir une 3/2-approximation :
--- trouver l'ensemble S'Ì S des noeuds de degré impair dans l'arbre minimal.
--- relier ces noeuds par un couplage minimal (les relier par paire en minimisant la longueur totale des arêtes ainsi crées [CLR90] (minimum matching)).
--- Le graphe obtenu en utilisant les arêtes du couplage minimal plus celle de l'arbre minimal est eulérien (tous les sommets on degré pair, certaines arêtes peuvent être présentes deux fois) on peut trouver un circuit utilisant chaque arête une et une seule fois.

Le circuit ainsi trouvé est au maximum 3/2 de fois plus long que le chemin optimal (le montrer).

3.2  Algorithmes et complexités

Le calcul de la triangulation de Delaunay décrit ici est en O(n2), la localisation par marche améliore les choses en pratique mais pas la complexité théorique dans le cas le pire. On pourra éventuellement programmer l'algorithme division-fusion (poly du cours de majeure "Géométrie et synthèse d'images" http://www-sop.inria.fr/personnel/devillers/x/).

La gestion de la queue de priorité peut-être faite soit en temps O(n2) avec une liste triée ou un arbre binaire non équilibré soit en O(nlogn) avec un arbre binaire équilibré.

Références

[BY95]
Jean-Daniel Boissonnat and Mariette Yvinec. Géométrie Algorithmique. Ediscience international, Paris, 1995.

[CLR90]
T. H. Cormen, C. E. Leiserson, and R. L. Rivest. Introduction to Algorithms. MIT Press, Cambridge, MA, 1990.
Ce document a été traduit de LATEX par HEVEA.