Chapitre 8 Exploration

Dans ce chapitre, on recherche des algorithmes pour résoudre des problèmes se présentant sous la forme suivante:

On se donne un ensemble E fini et à chaque élément e de E est affectée une valeur v(e) (en général, un entier positif), on se donne de plus un prédicat (une fonction à valeurs {vrai, faux}) C sur l'ensemble des parties de E. Le problème consiste à construire un sous ensemble F de E tel que:

C(F) est satisfait
S_{e Î F}v(e) soit maximal (ou minimal, dans certains cas)

Les méthodes développées pour résoudre ces problèmes sont de natures très diverses. Pour certains exemples, il existe un algorithme très simple consistant à initialiser F par F= Ø, puis à ajouter successivement des éléments suivant un certain critère, jusqu'à obtenir la solution optimale, c'est ce qu'on appelle l'algorithme glouton. Tous les problèmes ne sont pas résolubles par l'algorithme glouton mais, dans le cas où il s'applique, il est très efficace. Pour d'autres problèmes, c'est un algorithme dit de programmation dynamique qui permet d'obtenir la solution, il s'agit alors d'utiliser certaines particularités de la solution qui permettent de diviser le problème en deux; puis de résoudre séparément chacun des deux sous-problèmes, tout en conservant en table certaines informations intermédiaires. Cette technique, bien que moins efficace que l'algorithme glouton, donne quand même un résultat intéressant car l'algorithme mis en oeuvre est en général polynomial. Enfin, dans certains cas, aucune des deux méthodes précédentes ne donne de résultat et il faut alors utiliser des procédures d'exploration systématique de l'ensemble de toutes les parties de E satisfaisant C, cette exploration systématique est souvent appelée exploration arborescente (ou backtracking en anglais).

8.1 Algorithme glouton

Comme il a été dit, cet algorithme donne très rapidement un résultat. En revanche ce résultat n'est pas toujours la solution optimale. L'affectation d'une ou plusieurs ressource à des utilisateurs (clients, processeurs, etc.) constitue une classe importante de problèmes. Il s'agit de satisfaire au mieux certaines demandes d'accès à une ou plusieurs ressources, pendant une durée donnée, ou pendant une période de temps définie précisément. Le cas le plus simple de ces problèmes est celui d'une seule ressource, pour laquelle sont faites des demandes d'accès à des périodes déterminées. Nous allons montrer que dans ce cas très simple, l'algorithme glouton s'applique. Dans des cas plus complexes, l'algorithme donne une solution approchée, dont on se contente souvent, vu le temps de calcul prohibitif de la recherche de l'optimum exact.

8.1.1 Affectation d'une ressource

Le problème décrit précisément ci-dessous peut être résolu par l'algorithme glouton (mais, comme on le verra, l'algorithme glouton ne donne pas la solution optimale pour une autre formulation du problème, pourtant proche de celle-ci). Il s'agit d'affecter une ressource unique, non partageable, successivement à un certain nombre d'utilisateurs qui en font la demande en précisant la période exacte pendant laquelle ils souhaitent en disposer.

On peut matérialiser ceci en prenant pour illustration la location d'une seule voiture. Des clients formulent un ensemble de demandes de location et, pour chaque demande sont donnés le jour du début de la location et le jour de restitution du véhicule, le but est d'affecter le véhicule de façon à satisfaire le maximum de clients (et non pas de maximiser la somme des durées de location). On peut formuler ce problème en utilisant le cadre général considéré plus haut. L'ensemble E est celui des demandes de location, pour chaque élément e de E, on note d(e) la date du début de la location et f(e) > d(e) la date de fin. La valeur v(e) de tout élément e de E est égale à 1 et la contrainte à respecter pour le sous ensemble F à construire est la suivante:

" e₁,e₂ Î F d(e₁) £ d(e₂) Þ f(e₁) £ d(e₂)

puisque, disposant d'un seul véhicule, on ne peut le louer qu'à un seul client à la fois. L'algorithme glouton s'exprime comme suit:

Etape 1: Classer les éléments de E par ordre des dates de fins croissantes. Les éléments de E constituent alors une suite e₁, e₂, ... e_n telle que f(e₁) £ f(e₂), ... £ f(e_n)
Initialiser F := Ø
Etape 2: Pour i variant de 1 à n, ajouter la demande e_i à F si celle-ci ne chevauche pas la dernière demande appartenant à F.

Montrons que l'on a bien obtenu ainsi la solution optimale.

Soit F = {x₁, x₂, ... x_p} la solution obtenue par l'algorithme glouton et soit G = {y₁, y₂, ... y_q}, q ³ p une solution optimale. Dans les deux cas nous supposons que les demandes sont classées par dates de fins croissantes. Nous allons montrer que p=q. Supposons que " i <k, on ait x_i = y_i et que k soit le plus petit entier tel que x_k ¹ y_k, alors par construction de F on a: f(y_k) ³ f(x_k). On peut alors remplacer G par G' = {y₁, y₂, ... y_k-1, x_k,y_k+1, y_q} tout en satisfaisant à la contrainte de non chevauchement des demandes, ainsi G' est une solution optimale ayant plus d'éléments en commun avec F que n'en avait G. En répétant cette opération suffisamment de fois on trouve un ensemble H de même cardinalité que G et qui contient F. L'ensemble H ne peut contenir d'autres éléments car ceux-ci auraient été ajoutés à F par l'algorithme glouton, ceci montre bien que p=q.

Remarques

1. Noter que le choix de classer les demandes par dates de fin croissantes est important. Si on les avait classées, par exemple, par dates de début croissantes, on n'aurait pas obtenu le résultat. On le voit sur l'exemple suivant avec trois demandes e₁, e₂, e₃ dont les dates de début et de fin sont données par le tableau suivant:

	e₁	e₂	e₃
d	2	3	5
f	8	4	8

Bien entendu, pour des raisons évidentes de symétrie, le classement par dates de début décroissantes donne aussi le résultat optimal.

2. On peut noter aussi que si le but est de maximiser la durée totale de location du véhicule l'algorithme glouton ne donne pas l'optimum. En particulier, il ne considérera pas comme prioritaire une demande de location de durée très importante. L'idée est alors de classer les demandes par durées décroissantes et d'appliquer l'algorithme glouton, malheureusement cette technique ne donne pas non plus le bon résultat (il suffit de considérer une demande de location de 3 jours et deux demandes qui ne se chevauchent pas mais qui sont incompatibles avec la première chacune de durée égale à 2 jours). De fait, le problème de la maximisation de cette durée totale est NP complet, il est donc illusoire de penser trouver un algorithme simple et efficace.

3. S'il y a plus d'une ressource à affecter, par exemple deux voitures à louer, l'algorithme glouton consistant à classer les demandes suivant les dates de fin et à affecter la première ressource disponible, ne donne pas l'optimum.

8.1.2 Arbre recouvrant de poids minimal

Un exemple classique d'utilisation de l'algorithme glouton est la recherche d'un arbre recouvrant de poids minimal dans un graphe symétrique, il prend dans ce cas particulier le nom d'algorithme de Kruskal. Décrivons brièvement le problème et l'algorithme.

Un graphe symétrique est donné par un ensemble X de sommets et un ensemble A d'arcs tel que, pour tout a Î A, il existe un arc opposé a' dont l'origine est l'extrémité de a et dont l'extrémité est l'origine de a. Le couple {a, a'} forme une arête. Un arbre est un graphe symétrique tel que tout couple de sommets est relié par un chemin (connexité) et qui ne possède pas de circuit (autres que ceux formés par un arc et son opposé). Pour un graphe symétrique G= (X,A) quelconque, un arbre recouvrant est donné par un sous ensemble de l'ensemble des arêtes qui forme un arbre ayant X pour ensemble de sommets (voir figure 8.1). Pour posséder un arbre recouvrant, un graphe doit être connexe. Dans ce cas, les arborescences construites par les algorithmes décrits au chapitre 5 sont des arbres recouvrants. Lorsque chaque arête du graphe est affectée d'un certain poids, se pose le problème de la recherche d'un arbre recouvrant de poids minimal (c'est à dire un arbre dont la somme des poids des arêtes soit minimale). Une illustration de ce problème est la réalisation d'un réseau électrique ou informatique entre différents points, deux points quelconques doivent toujours être reliés entre eux (connexité) et on doit minimiser le coût de la réalisation. Le poids d'une arête est, dans ce contexte, le coût de construction de la portion du réseau reliant ses deux extrémités.

Figure 8.1 : Un graphe symétrique et l'un de ses arbres recouvrants

On peut facilement formuler le problème dans le cadre général donné en début de chapitre: E est l'ensemble des arêtes du graphe, la condition C à satisfaire par F est de former un graphe connexe, enfin il faut minimiser la somme des poids des éléments de F. Ce problème peut être résolu très efficacement par l'algorithme glouton suivant :

Etape 1: Classer les arêtes par ordre de poids croissants. Elles constituent alors une suite
e₁, e₂, ... e_n
telle que
p(e₁) £ p(e₂), ... £ p(e_n)
Initialiser F := Ø
Etape 2: Pour i variant de 1 à n, ajouter l'arête e_i à F si celle-ci ne crée pas de circuit avec celles appartenant à F.

On montre que l'algorithme glouton donne l'arbre de poids minimal en utilisant la propriété suivante des arbres recouvrants d'un graphe:

Soient T et U deux arbres recouvrants distincts d'un graphe G et soit a une arête de U qui n'est pas dans T. Alors il existe une arête b de T telle que U \ {a }È {b } soit aussi un arbre recouvrant de G.

Plus généralement on montre que l'algorithme glouton donne le résultat si et seulement si la propriété suivante est vérifiée par les sous ensembles F de E satisfaisant C:

Si F et G sont deux ensembles qui satisfont la condition C et si x est un élément qui est dans F et qui n'est pas dans G, alors il existe un élément de G tel que F \ {x}È {y } satisfasse C.

Un exemple d'arbre recouvrant de poids minimal est donné sur la figure 8.2.

Figure 8.2 : Un arbre recouvrant de poids minimum

8.2 Exploration arborescente

De très nombreux problèmes d'optimisation ou de recherche de configurations particulières donnent lieu à un algorithme qui consiste à faire une recherche exhaustive des solutions. Ces algorithmes paraissent simples puisqu'il s'agit de parcourir systématiquement un ensemble de solutions, mais bien que leur principe ne soit pas particulièrement ingénieux, la programmation nécessite un certain soin.

8.2.1 Sac à dos

Prenons pour premier exemple le problème dit du sac à dos; soit un ensemble E d'objets chacun ayant un certain poids, un entier positif noté p(e), et soit M un réel qui représente la charge maximum que l'on peut emporter dans un sac à dos. La question est de trouver un ensemble d'objets dont la somme des poids soit la plus voisine possible de M tout en lui étant inférieure ou égale. Le problème est ici formulé dans les termes généraux du début du chapitre, la condition C portant sur le poids du sac à ne pas dépasser. Il est assez facile de trouver des exemples pour lesquels l'algorithme glouton ne donne pas le bon résultat, il suffit en effet de considérer 4 objets de poids respectifs 4,3,3,1 pour remplir un sac de charge maximum égale à 6. On s'apperçoit que si l'on remplit le sac en présentant les objets en ordre de poids décroissants et en retenant ceux qui ne font pas dépasser la capacité maximale, on obtiendra une charge égale à 5. Si à l'opposé, on classe les objets par ordre de poids croissants, et que l'on applique l'algorithme glouton, la charge obtenue sera égale à 4, alors qu'il est possible de remplir le sac avec deux objets de poids 3 et d'obtenir l'optimum.

Le problème du sac à dos, lorsque la capacité du sac n'est pas un entier, ¹ est un exemple typique classique de problème (NP-complet) pour lequel aucun algorithme efficace n'est connu et où il faut explorer toutes les possibilités pour obtenir la meilleure solution. Une bonne programmation de cette exploration systématique consiste à utiliser la récursivité. Notons n le nombre d'éléments de E, nous utiliserons un tableau sac permettant de coder toutes les possibilités, un objet i est mis dans le sac si sac[i] = true, il n'est pas mis si sac[i] = false. Il faut donc parcourir tous les vecteurs possibles de booléens, pour cela on considère successivement toutes les positions i= 1, ... n et on effectue les deux choix possibles pour sac[i] en ne choisissant pas la dernière possibilité si l'on dépasse la capacité du sac. On utilise un entier meilleur qui mémorise la plus petite valeur trouvée pour la différence entre la capacité du sac et la somme des poids des objets qui s'y trouvent. Un tableau msac garde en mémoire le contenu du sac qui réalise ce minimum. La procédure récursive calcul(i,u) a pour paramètres d'appel, i l'objet pour lequel on doit prendre une décision, et u la capacité disponible restante. Elle considère deux possibilités pour l'objet i l'une pour laquelle il est mis dans le sac (si on ne dépasse pas la capacité restante u), l'autre pour laquelle il n'y est pas mis. La procédure appelle calcul(i+1, u) et calcul(i+1, u - p[i]). Ainsi le premier appel de calcul(i, u) est fait avec i = 0 et u égal à la capacité M du sac, les appels successifs feront ensuite augmenter i (et diminuer u) jusqu'à atteindre la valeur n. Le résultat est mémorisé s'il améliore la valeur courante de meilleur.

static void calcul (int i, float u) {
    if (i >= n) {
        if (u < meilleur) {
            for (int j = 0; i < n; ++i)
                msac[i] = sac[i];
            meilleur = u;
        }
    } else {
        if  (p[i] <= u) {
            sac[i] = true;
            calcul(i + 1, u - p[i]);
        }
        sac[i] = false;
        calcul(i + 1, u);
    }
}

On vérifie sur des exemples que cette procédure donne des résultats assez rapidement pour n £ 20. Pour des valeurs plus grandes le temps mis est bien plus long car il croît comme 2ⁿ.

8.2.2 Placement de reines sur un échiquier

Le placement de reines sur un échiquier sans qu'aucune d'entre elles ne soit en prise par une autre constitue un autre exemple de recherche arborescente. Là encore il faut parcourir l'ensemble des solutions possibles. Pour les valeurs successives de i, on place une reine sur la ligne i et sur une colonne j = pos[i] en vérifiant bien qu'elle n'est pas en prise. Le tableau pos que l'on remplit récursivement contient les positions des reines déjà placées. Tester si deux reines sont en conflit est relativement simple. Notons i₁,j₁ et i₂, j₂ leurs positions respectives (ligne et colonne) il y a conflit si i₁ = i₂ (elles sont alors sur la même ligne), ou si j₁ = j₂ (même colonne) ou si |i₁ - i₂ | = |j₁ -j₂| (même diagonale).

static boolean conflit (int i1, int j1, int i2, int j2) {

  return (i1 == i2) || (j1 == j2) ||
         (Math.abs (i1 - i2) == Math.abs (j1 - j2));
}

Celle-ci peut être appelée plusieurs fois pour tester si une reine en position i, j est compatible avec les reines précédemment placées sur les lignes 1, ..., i - 1:

static boolean compatible (int i, int j) {

    for (int k = 0; k < i; ++k) 
        if (conflit (i, j, k, pos[k]))
            return false;
    return true;
}

Figure 8.3 : Huit reines sur un échiquier

La fonction récursive qui trouve une solution au problème des reines est alors la suivante:

static void reines (int i) {

  if (i >= nbReines)
      imprimerSolution();
  else {
      for (int j = 0; j < nbReines; ++j)
          if compatible (i, j) {
              pos[i] = j;
              reines (i+1);
          }
  }
}

La boucle for à l'intérieur de la procédure permet de parcourir toutes les positions sur la ligne i compatibles avec les reines déjà placées. Les appels successifs de Reines(i) modifient la valeur de pos[i] déterminée par l'appel précédent. La procédure précédente affiche toutes les solutions possibles, il est assez facile de modifier la procédure en s'arrêtant dès que l'on a trouvé une solution ou pour simplement compter le nombre de solutions différentes. En lançant Reines(0), on trouve ainsi 90 solutions pour un échiquier 8 × 8 dont l'une d'elles est donnée figure 8.3.

Remarque

Dans les deux exemples donnés plus haut, toute la difficulté réside dans le parcours de toutes les solutions possibles, sans en oublier et sans revenir plusieurs fois sur la même. On peut noter que l'ensemble de ces solutions peut être vu comme les sommets d'une arborescence qu'il faut parcourir. La différence avec les algorithmes décrits au chapitre 5 est que l'on ne représente pas cette arborescence en totalité en mémoire mais simplement la partie sur laquelle on se trouve.

8.3 Programmation dynamique

Pour illustrer la technique d'exploration appelée programmation dynamique, le mieux est de commencer par un exemple. Nous considérons ainsi la recherche de chemins de longueur minimale entre tous les couples de points d'un graphe aux arcs valués.

8.3.1 Plus courts chemins dans un graphe

Dans la suite, on considère un graphe G= (X,A) ayant X comme ensemble de sommets et A comme ensemble d'arcs. On se donne une application l de A dans l'ensemble des entiers naturels, l(a) est la longueur de l'arc a. La longueur d'un chemin est égale à la somme des longueurs des arcs qui le composent. Le problème consiste à déterminer pour chaque couple (x_i, x_j) de sommets, le plus court chemin, s'il existe, qui joint x_i à x_j. Nous commençons par donner un algorithme qui détermine les longueurs des plus courts chemins notées d(x_i, x_j); on convient de noter d(x_i, x_j)= ¥ s'il n'existe pas de chemin entre x_i et x_j (en fait il suffit dans la suite de remplacer ¥ par un nombre suffisamment grand par exemple la somme des longueurs de tous les arcs du graphe). La construction effective des chemins sera examinée ensuite. On suppose qu'entre deux sommets il y a au plus un arc. En effet, s'il en existe plusieurs, il suffit de ne retenir que le plus court.

Les algorithmes de recherche de chemins les plus courts reposent sur l'observation très simple mais importante suivante:

Remarque

Si f est un chemin de longueur minimale joignant x à y et qui passe par z, alors il se décompose en deux chemins de longueur minimale l'un qui joint x à z et l'autre qui joint z à y.

Dans la suite, on suppose les sommets numérotés x₁, x₂, ... x_n et, pour tout k>0 on considère la propriété P_k suivante pour un chemin:

(P_k(f)) Tous les sommets de f, autres que son origine et son extrémité, ont un indice strictement inférieur à k.

On peut remarquer qu'un chemin vérifie P₁ si et seulement s'il se compose d'un unique arc, d'autre part la condition P_n+1 est satisfaite par tous les chemins du graphe. Notons d_k (x_i,x_j) la longueur du plus court chemin qui vérifie P_k et qui a pour origine x_i et pour extrémité x_j. Cette valeur est ¥ si aucun tel chemin n'existe. Ainsi d₁(x_i,x_j)= ¥ s'il n'y a pas d'arc entre x_i et x_j et vaut l(a) si a est cet arc. D'autre part d_n+1 = d. Le lemme suivant permet de calculer les d_k+1 connaissant les d_k (x_i,x_j). On en déduira un algorithme itératif.

Lemme

Les relations suivantes sont satisfaites par les d_k:

d_k+1(x_i, x_j) = min(d_k(x_i,x_j), d_k(x_i,x_k) +d_k(x_k,x_j))

Preuve

Soit un chemin de longueur minimale satisfaisant P_k+1, ou bien il ne passe pas par x_k et on a

d_k+1(x_i, x_j) = d_k(x_i,x_j)

ou bien il passe par x_k et, d'après la remarque préliminaire, il est composé d'un chemin de longueur minimale joignant x_i à x_k et satisfaisant P_k et d'un autre minimal aussi joignant x_k à x_j. Il a donc pour longueur: d_k(x_i,x_k) +d_k(x_k,x_j).

L'algorithme suivant pour la recherche du plus court chemin met à jour une matrice delta[i,j] qui a été initialisée par les longueurs des arcs et par un entier suffisamment grand s'il n'y a pas d'arc entre x_i et x_j. A chaque itération de la boucle externe, on fait croître l'indice k du d_k calculé.

for (k = 0; k < n; ++k)
   for (i = 0; i < n; ++i)
      for (j = 1; j < n; ++j)
         delta[i][j] = Math.min(delta[i][j], delta[i][k] + delta[k][j]);

On note la similitude avec l'algorithme de recherche de la fermeture transitive d'un graphe exposé au chapitre 5. Sur l'exemple du graphe donné sur la figure 8.4, on part de la matrice d₁ donnée par

d₁=

æ
ç
ç
ç
ç
ç
ç
ç
è

0	1	¥	4	¥	¥	¥
¥	0	3	2	¥	¥	¥
¥	¥	0	¥	2	¥	¥
¥	¥	¥	0	2	¥	6
¥	3	¥	¥	0	1	¥
¥	¥	¥	2	¥	0	1
4	¥	¥	¥	¥	¥	0

ö
÷
÷
÷
÷
÷
÷
÷
ø

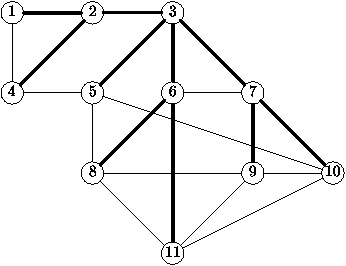
Figure 8.4 : Un graphe aux arcs valués

Après le calcul on obtient:

d =

æ
ç
ç
ç
ç
ç
ç
ç
è

0	1	4	3	5	6	7
10	0	3	2	4	5	6
8	5	0	5	2	3	4
8	5	8	0	2	3	4
6	3	6	3	0	1	2
5	6	9	2	4	0	1
4	5	8	7	9	10	0

ö
÷
÷
÷
÷
÷
÷
÷
ø

Pour le calcul effectif des chemins les plus courts, on utilise une matrice qui contient Suiv[i,j], le sommet qui suit i dans le chemin le plus court qui va de i à j. Les valeurs Suiv[i,j] sont initialisées à j s'il existe un arc de i vers j et à -1 sinon, Suiv[i,i] est lui initialisé à i. Le calcul précédent qui a donné d peut s'accompagner de celui de Suiv en procédant comme suit:

for (int k = 0; k < n; ++k)
    for (int i = 0; i < n; ++i)
        for (int j = 0; j < n; ++j)
          if (delta[i][j] > (delta[i][k] + delta[k][j]) {
              delta[i][j] =  delta[i][k] + delta[k][j]; 
              suivant[i][j] = suivant[i][k];
          }

Une fois le calcul des deux matrices effectué on peut retrouver le chemin le plus court qui joint i à j par la procédure:

static void plusCourtChemin(int i, int j) {

  for (int k = i; k != j; k = suivant[k][j])
      System.out.print (k + " ");
  System.out.println (j);
}

Sur l'exemple précédent on trouve:

Suiv =

æ
ç
ç
ç
ç
ç
ç
ç
è

1	2	2	2	2	2	2
4	2	3	4	4	4	4
5	5	3	5	5	5	5
5	5	5	4	5	5	5
6	2	2	6	5	6	6
7	7	7	4	4	6	7
1	1	1	1	1	1	7

ö
÷
÷
÷
÷
÷
÷
÷
ø

8.3.2 Sous-séquences communes

On utilise aussi un algorithme de programmation dynamique pour rechercher des sous-séquences communes à deux séquences données. précisons tout d'abord quelques définitions. Une séquence (ou un mot) est une suite finie de symboles (ou lettres) pris dans un ensemble fini (ou alphabet). Si u=a₁··· a_n est une séquence, où a₁,... ,a_n sont des lettres, l'entier n est la longueur de u. Une séquence v=b₁··· b_m est une sous-séquence de u=a₁··· a_n s'il existe des entiers i₁,... ,i_m, (1£ i₁<··· i_m£ n) tels que a_{i_k}=b_k (1£ k£ m). Une séquence w est une sous-séquence commune aux séquences u et v si w est sous-séquence de u et de v. Une sous-séquence commune est maximale si elle est de longueur maximale.

On cherche à déterminer la longueur d'une sous-séquence commune maximale à u=a₁··· a_n et v=b₁··· b_m. Pour cela, on note L(i,j) la longueur d'une sous-séquence commune maximale aux mots a₁··· a_i et b₁··· b_j, (0£ j£ m, 0£ i£ n). On peut montrer que

L(i,j)=

ì
í
î

1 + L(i-1,j-1)	si a_i=b_j
max (L(i,j-1),L(i-1,j))	sinon.

(*)

En effet, soit w une sous séquence de longueur maximale, commune à a₁··· a_i-1 et à b₁··· b_j-1 si a_i = b_j, wa_i est une sous-séquence commune maximale à a₁··· a_i et b₁··· b_j. Si a_i ¹ b_j alors une sous-séquence commune à a₁··· a_i et b₁··· b_j est ou bien commune à a₁··· a_i et b₁··· b_j-1 (si elle ne se termine pas par b_j); ou bien à a₁··· a_i-1 et b₁··· b_j, (si elle ne se termine par a_i). On obtient ainsi l'algorithme qui permet de déterminer la longueur d'une sous séquence commune maximale à a₁··· a_n et b₁··· b_m

static void longueurSSC (String u, String v) {

  int n = u.length();
  int m = v.length();
  int longueur[][] = new int[n][m];
  for (int i = 0; i < n; ++i) longueur[i, 0] = 0;
  for (int j = 0; j < m; ++j) longueur[0, j] = 0;
  for (int i = 1; i < n; ++i)
      for (int j = 1; j < m; ++j)
          if (u.charAt(i) == v.charAt(j))
               longueur[i][j] = 1 + longueur[i-1][j-1];
          else if longueur[i][j-1] > longueur[i-1][j] 
               longueur[i][j] = longueur[i][j-1];
          else
               longueur[i][j] = longueur[i-1][j];
}

Il est assez facile de transformer l'algorithme pour retrouver une sous-séquence maximale commune au lieu de simplement calculer sa longueur. Pour cela, on met à jour un tableau provient qui indique lequel des trois cas a permis d'obtenir la longueur maximale.

static void longueurSSC (String u, String v, 
                         int[][] longueur, int[][] provient) {
  int n = u.length();
  int m = v.length();
  for (int i = 0; i < n; ++i) longueur[i, 0] = 0;
  for (int j = 0; j < m; ++j) longueur[0, j] = 0;
  for (int i = 1; i < n; ++i)
      for (int j = 1; j < m; ++j)
          if (u.charAt(i) == v.charAt(j)) {
               longueur[i][j] = 1 + longueur[i-1][j-1];
               provient[i,j] = 1;
          } else if longueur[i][j-1] > longueur[i-1][j] {
               longueur[i][j] = longueur[i][j-1];
               provient[i,j] = 2;
          } else {
               longueur[i][j] = longueur[i-1][j];
               provient[i,j] = 3
          }
}

Une fois ce calcul effectué il suffit de remonter à chaque étape de i,j vers i-1, j-1, vers i, j-1 ou vers i-1,j en se servant de la valeur de provient[i,j].

static String ssc (String u, String v) {

  int n = u.length();
  int m = v.length();
  int longueur[][] = new int[n][m];
  int provient[][] = new int[n][m];
  longueurSSC (u, v, longueur, provient);

  int lg = longueur[n][m];
  StringBuffer res = new StringBuffer(lg);
  int i = n, j = m;
  for (int k = lg-1; k >= 0; ) 
      switch (provient[i][j]) {
      case 1: res.setCharAt(k, u.charAt(i-1)); --i; --j; --k; 
              break;
      case 2: --j; break;
      case 3: --i; break;
      }
  return new String(res);
}

Remarque

La recherche de sous-séquences communes à deux séquences intervient parmi les nombreux problèmes algorithmiques posés par la recherche des propriétés des séquences représentant le génome humain.

8.4 Programmes en Caml

(* les n reines, voir page X *)

let nReines n =
  let pos = make_vect n 0 in

  let conflit i1 j1 i2 j2 =
    i1 = i2 || j1 = j2 ||
    abs(i1 - i2) = abs (j1 - j2) in

  let compatible i j =
    try 
      for k = 0 to i-1 do
        if conflit i j k pos.(k) then
           raise Exit
      done;
      true
    with Exit -> false in

  let rec reines i =
    if i >= n then 
      imprimerSolution pos
    else
      for j = 0 to n-1 do
        if compatible i j then begin
          pos.(i) <- j;
          reines (i+1);
        end
      done in

  reines 0;;

(* les n reines (suite) *)
#open "printf";;

let imprimerSolution pos =
  let n = vect_length(pos) in
  for i = 0 to n-1 do
    for j = 0 to n-1 do
      if j = pos.(i) then
        printf "* "
      else
        printf "  "
     done;
     printf "\n";
   done;
   printf "----------------------\n";;

(* les sous séquences communes *)
let longueur_ssc u v =
   let n = string_length u and
       m = string_length v in
   let longueur = make_matrix (n+1) (m+1) 0 and
       provient = make_matrix (n+1) (m+1) 0 in
   for i=1 to n do 
     for j=1 to m do
       if u.[i-1] = v.[j-1] then begin
         longueur.(i).(j) <- 1 + longueur.(i-1).(j-1);
         provient.(i).(j) <- 1;
       end else
       if longueur.(i).(j-1) > longueur.(i-1).(j) then begin
         longueur.(i).(j) <- longueur.(i).(j-1);
         provient.(i).(j) <- 2;
       end else begin
         longueur.(i).(j) <- longueur.(i-1).(j);
         provient.(i).(j) <- 3;
       end
     done
   done;
   longueur, provient;;

let ssc u v =
  let n = string_length u and
      m = string_length v in
  let longueur, provient = longueur_ssc u v in
  let lg = longueur.(n).(m) in
  let res = create_string lg and
      i = ref n and
      j = ref m and
      k = ref (lg-1) in
  while !k >= 0 do
    match provient.(!i).(!j) with
      1 -> res.[!k] <- u.[!i-1]; decr i; decr j; decr k
    | 2 -> decr j
    | _ -> decr i
  done;
  res;;

1: Dans le cas où M est en entier, on peut trouver un algorithme très efficace fondé sur la programmation dynamique.