Chapitre 2 Récursivité

Les définitions par récurrence sont assez courantes en mathématiques. Prenons le cas de la suite de Fibonacci, définie par

u₀ = u₁ = 1

u_n = u_n-1 + u_n-2 pour n > 1

On obtient donc la suite 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946,...Nous allons voir que ces définitions s'implémentent très simplement en informatique par les définitions récursives.

2.1 Fonctions récursives

2.1.1 Fonctions numériques

Pour calculer la suite de Fibonacci, une transcription littérale de la formule est la suivante:

static int fib (int n) {

  if (n <= 1)
      return 1;
  else
      return fib (n-1) + fib (n-2);
}

fib est une fonction qui utilise son propre nom dans la définition d'elle-même. Ainsi, si l'argument n est plus petit que 1, on retourne comme valeur 1. Sinon, le résultat est fib(n-1) + fib(n-2). Il est donc possible en Java, comme en beaucoup d'autres langages (sauf Fortran), de définir de telles fonctions récursives. D'ailleurs, toute suite á u_n ñ définie par récurrence s'écrit de cette manière en Java, comme le confirment les exemples numériques suivants: factorielle et le triangle de Pascal.

static int fact(int n)  {             

  if (n <= 1)
      return 1;
  else
      return n * fact (n-1);
}

static int C(int n, int p)  {         

  if ((n == 0) || (p == n))
      return 1;
  else
      return C(n-1, p-1) + C(n-1, p);
}

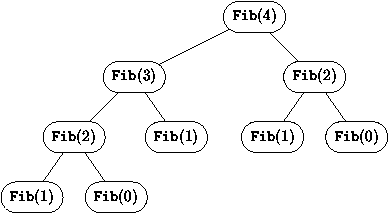
On peut se demander comment Java s'y prend pour faire le calcul des fonctions récursives. Nous allons essayer de le suivre sur le calcul de fib(4). Rappelons nous que les arguments sont transmis par valeur dans le cas présent, et donc qu'un appel de fonction consiste à évaluer l'argument, puis à se lancer dans l'exécution de la fonction avec la valeur de l'argument. Donc

fib(4) -> fib (3) + fib (2)
       -> (fib (2) + fib (1)) + fib (2)
       -> ((fib (1) + fib (1)) + fib (1)) + fib(2)
       -> ((1 + fib(1)) + fib (1)) + fib(2)
       -> ((1 + 1) + fib (1)) + fib(2)
       -> (2 + fib(1)) + fib(2)
       -> (2 + 1) + fib(2) 
       -> 3 + fib(2)
       -> 3 + (fib (1) + fib (1))
       -> 3 + (1 + fib(1))
       -> 3 + (1 + 1)
       -> 3 + 2
       -> 5

Figure 2.1 : Appels récursifs pour fib(4)

Il y a donc un bon nombre d'appels successifs à la fonction fib (9 pour fib(4)). Comptons le nombre d'appels récursifs R_n pour cette fonction. Clairement R₀ = R₁ = 1, et R_n = 1 + R_n-1 + R_n-2 pour n > 1. En posant R'_n = R_n + 1, on en déduit que R'_n = R'_n-1+ R'_n-2 pour n > 1, R'₁ = R'₀ = 2. D'où R'_n = 2 × fib(n), et donc le nombre d'appels récursifs R_n vaut 2 × fib(n) - 1, c'est à dire 1, 1, 3, 5, 9, 15, 25, 41, 67, 109, 177, 287, 465, 753, 1219, 1973, 3193, 5167, 8361, 13529, 21891,... Le nombre d'appels récursifs est donc très élevé, d'autant plus qu'il existe une méthode itérative simple en calculant simultanément fib(n) et fib(n-1). En effet, on a un calcul linéaire simple

æ
è

fib(n)

fib(n-1)

ö
ø

æ
è

1		1
1		0

ö
ø

æ
è

fib(n-1)

fib(n-2)

ö
ø

Ce qui donne le programme itératif suivant

static int fib(int n)  {

  int u, v;
  int u0, v0;
  int i;

  u = 1; v = 1;
  for (i = 2; i <= n; ++i) {
      u0 = u; v0 = v;
      u = u0 + v0;
      v = v0;
  }
  return u;
}

Pour résumer, une bonne règle est de ne pas trop essayer de suivre dans les moindres détails les appels récursifs pour comprendre le sens d'une fonction récursive. Il vaut mieux en général comprendre synthétiquement la fonction. La fonction de Fibonacci est un cas particulier car son calcul récursif est particulièrement long. Mais ce n'est pas le cas en général. Non seulement, l'écriture récursive peut se révéler efficace, mais elle est toujours plus naturelle et donc plus esthétique. Elle ne fait que suivre les définitions mathématiques par récurrence. C'est une méthode de programmation très puissante.

2.1.2 La fonction d'Ackermann

La suite de Fibonacci avait une croissance exponentielle. Il existe des fonctions récursives qui croissent encore plus rapidement. Le prototype est la fonction d'Ackermann. Au lieu de définir cette fonction mathématiquement, il est aussi simple d'en donner la définition récursive en Java

static int ack(int m, int n) {

  if (m == 0)
      return n + 1;
  else
      if (n == 0)
          return ack (m - 1, 1);
      else
          return ack (m - 1, ack (m, n - 1));
}

On peut vérifier que

ack(0, n) = n + 1

ack(1, n) = n + 2

ack(2, n) » 2 * n

ack(3, n) » 2 n

ack(4, n) » 2

·^·^{^·}^{^²}

ü
ý
þ

Donc ack(5, 1) » ack(4, 4) » 2⁶⁵⁵³⁶ > 10⁸⁰, c'est à dire le nombre d'atomes de l'univers.

2.1.3 Récursion imbriquée

La fonction d'Ackermann contient deux appels récursifs imbriqués, c'est ce qui la fait croître si rapidement. Un autre exemple est la fonction 91 de MacCarthy

static int f(int n)  {

  if (n > 100)
      return n - 10; 
  else
      return f(f(n+11));        
}

Ainsi, le calcul de f(96) donne f(96) = f(f(107)) = f(97) = ··· f(100) = f(f(111)) = f(101) = 91. On peut montrer que cette fonction vaut 91 si n £ 100 et n - 10 si n > 100. Cette fonction anecdotique, qui utilise la récursivité imbriquée, est intéressante car il n'est pas du tout évident qu'une telle définition donne toujours un résultat.¹ Par exemple, la fonction de Morris suivante

static int g(int m, int n) {

  if (m == 0)
      return 1; 
  else
      return g(m - 1, g(m, n));      
}

Que vaut alors g(1, 0)? En effet, on a g(1, 0) = g(0, g(1, 0)). Il faut se souvenir que Java passe les arguments des fonctions par valeur. On calcule donc toujours la valeur de l'argument avant de trouver le résultat d'une fonction. Dans le cas présent, le calcul de g(1,0) doit recalculer g(1, 0). Et le calcul ne termine pas.

2.2 Indécidabilité de la terminaison

Les logiciens Gödel et Turing ont démontré dans les années 30 qu'il était impossible d'espérer trouver un programme sachant tester si une fonction récursive termine son calcul. L'arrêt d'un calcul est en effet indécidable. Dans cette section, nous montrons qu'il n'existe pas de fonction qui permette de tester si une fonction Java termine. Nous présentons cette preuve sous la forme d'une petite histoire:

Le responsable des travaux pratiques d'Informatique en a assez des programmes qui calculent indéfiniment écrits par des élèves peu expérimentés. Cela l'oblige à chaque fois à des manipulations compliquées pour stopper ces programmes. Il voit alors dans un journal spécialisé une publicité:

Ne laissez plus boucler vos programmes! Utilisez notre fonction termine(o). Elle prend comme paramètre le nom d'un objet et répond true si la procédure f de cet objet ne boucle pas indéfiniment et false sinon. En n'utilisant que les procédures pour lesquelles termine répond true, vous évitez tous les problèmes de non terminaison. D'ailleurs, voici quelques exemples:

class Turing {

  static boolean termine (Object o) {
      // détermine la terminaison de o.f()
      boolean resultat;
      // contenu breveté par le vendeur
      return resultat;
  }
}

class Facile { 
  void f () {
  }
}

class Boucle {
  void f () {
      for (int i = 1; i > 0; ++i)
          ;
  }
}

class Test {
  public static void main (String args[]) {
      Facile o1 = new Facile();
      System.out.println (Turing.termine(o1));
      Boucle o2 = new Boucle();
      System.out.println (Turing.termine(o2));
  }
}

pour lesquels termine(o) répond true puis false.

Impressionné par la publicité, le responsable des travaux pratiques achète à prix d'or cette petite merveille et pense que sa vie d'enseignant va être enfin tranquille. Un élève lui fait toutefois remarquer qu'il ne comprend pas l'acquisition faite par le Maître avec la classe suivante:

class Absurde {
  void f () {
      while (Turing.termine(this))
          ;
   }

class Test {
  public static void main (String args[]) {
      Absurde o3 = new Absurde();
      System.out.println (Turing.termine(o3));
  }
}

Si la procédure o3.f boucle indéfiniment, alors termine(o3) = false. Donc la boucle while de o3.f s'arrête et o3.f termine. Sinon, si la procédure o3.f ne boucle pas indéfiniment, alors termine(o3) = true. La boucle while précédente boucle indéfiniment, et la procédure o3.f boucle indéfiniment. Il y a donc une contradiction sur les valeurs possibles de termine(o3). Cette expression ne peut être définie. Ayant noté le mauvais esprit de l'Elève, le Maître conclut qu'on ne peut décidément pas faire confiance à la presse spécialisée!

L'histoire est presque vraie. Le Maître s'appelait David Hilbert et voulait montrer la validité de sa thèse par des moyens automatiques. L'Elève impertinent était Kurt Gödel. Le tout se passait vers 1930. Grâce à Gödel, on s'est rendu compte que toutes les fonctions mathématiques ne sont pas calculables par programme. Par exemple, il y a beaucoup plus de fonctions de N (entiers naturels) dans N que de programmes qui sont en quantité dénombrable. Gödel, Turing, Church et Kleene sont parmi les fondateurs de la théorie de la calculabilité.

Pour être plus précis, on peut remarquer que nous demandons beaucoup à notre fonction termine, puisqu'elle prend en argument un objet (en fait une ``adresse mémoire''), désassemble peut-être la procédure correspondante, et décide de sa terminaison. Sinon, elle ne peut que lancer l'exécution de son argument et ne peut donc tester sa terminaison (quand il ne termine pas). Un résultat plus fort peut être montré: il n'existe pas de fonction prenant en argument le source de toute procédure (en tant que chaîne de caractères) et décidant de sa terminaison. C'est ce résultat qui est couramment appelé l'indécidabilité de l'arrêt. Mais montrer la contradiction en Java est alors beaucoup plus dur.

2.3 Procédures récursives

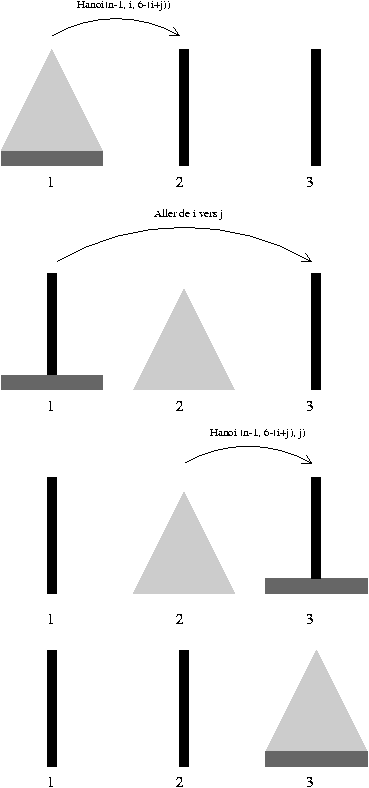
Figure 2.2 : Les tours de Hanoi

Les procédures, comme les fonctions, peuvent être récursives, et comporter un appel récursif. L'exemple le plus classique est celui des tours de Hanoi. On a 3 piquets en face de soi, numérotés 1, 2 et 3 de la gauche vers la droite, et n rondelles de tailles toutes différentes entourant le piquet 1, formant un cône avec la plus grosse en bas et la plus petite en haut. On veut amener toutes les rondelles du piquet 1 au piquet 3 en ne prenant qu'une seule rondelle à la fois, et en s'arrangeant pour qu'à tout moment il n'y ait jamais une rondelle sous une plus grosse. La légende dit que les bonzes passaient leur vie à Hanoi à résoudre ce problème pour n=64, ce qui leur permettait d'attendre l'écroulement du temple de Brahma, et donc la fin du monde (cette légende fut inventée par le mathématicien français E. Lucas en 1883). Un raisonnement par récurrence permet de trouver la solution en quelques lignes. Si n £ 1, le problème est trivial. Supposons maintenant le problème résolu pour n-1 rondelles pour aller du piquet i au piquet j. Alors, il y a une solution très facile pour transférer n rondelles de i en j:
1- on amène les n-1 rondelles du haut de i sur le troisième piquet k = 6 - i - j,
2- on prend la grande rondelle en bas de i et on la met toute seule en j,
3- on amène les n-1 rondelles de k en j.
Ceci s'écrit

static void hanoi(int n, int i, int j)  {

  if (n > 0) {
      hanoi (n-1, i, 6-(i+j));
      System.out.println (i + " -> " + j);
      hanoi (n-1, 6-(i+j), j);
  }
}

Ces quelques lignes de programme montrent bien comment en généralisant le problème, c'est-à-dire aller de tout piquet i à tout autre j, un programme récursif de quelques lignes peut résoudre un problème a priori compliqué. C'est la force de la récursion et du raisonnement par récurrence. Il y a bien d'autres exemples de programmation récursive, et la puissance de cette méthode de programmation a été étudiée dans la théorie dite de la récursivité qui s'est développée bien avant l'apparition de l'informatique (Kleene [25], Rogers [45]). Le mot récursivité n'a qu'un lointain rapport avec celui qui est employé ici, car il s'agissait d'établir une théorie abstraite de la calculabilité, c'est à dire de définir mathématiquement les objets qu'on sait calculer, et surtout ceux qu'on ne sait pas calculer. Mais l'idée initiale de la récursivité est certainement à attribuer à Kleene (1935).

2.4 Fractales

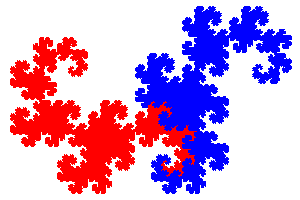
Considérons d'autres exemples de programmes récursifs. Des exemples spectaculaires sont le cas de fonctions graphiques fractales. Nous utilisons les fonctions graphiques du Macintosh (cf. page X). Un premier exemple simple est le flocon de von Koch [11] qui est défini comme suit

Figure 2.3 : Flocons de von Koch

Le flocon d'ordre 0 est un triangle équilatéral.
Le flocon d'ordre 1 est ce même triangle dont les côtés sont découpés en trois et sur lequel s'appuie un autre triangle équilatéral au milieu.
Le flocon d'ordre n+1 consiste à prendre le flocon d'ordre n en appliquant la même opération sur chacun de ses côtés.

Le résultat ressemble effectivement à un flocon de neige idéalisé. L'écriture du programme est laissé en exercice. On y arrive très simplement en utilisant les fonctions trigonométriques sin et cos. Un autre exemple classique est la courbe du Dragon. La définition de cette courbe est la suivante: la courbe du Dragon d'ordre 1 est un vecteur entre deux points quelconques P et Q, la courbe du Dragon d'ordre n est la courbe du Dragon d'ordre n-1 entre P et R suivie de la même courbe d'ordre n-1 entre R et Q (à l'envers), où PRQ est le triangle isocèle rectangle en R, et R est à droite du vecteur PQ. Donc, si P et Q sont les points de coordonnées (x, y) et (z,t), les coordonnées (u, v) de R sont

u = (x + z)/2 + (t - y)/2

v = (y + t)/2 - (z - x)/2

Figure 2.4 : La courbe du Dragon

La courbe se programme simplement par

static void dragon(int n, int x, int y, int z, int t) {

  int u, v;

  if (n == 1) {
      moveTo (x, y);
      lineTo (z, t);
  } else {
      u = (x + z + t - y) / 2;
      v = (y + t - z + x) / 2;
      dragon (n-1, x, y, u, v);
      dragon (n-1, z, t, u, v);
  }
}

Si on calcule dragon (20, 20, 20, 220, 220), on voit apparaître un petit dragon. Cette courbe est ce que l'on obtient en pliant 10 fois une feuille de papier, puis en la dépliant. Une autre remarque est que ce tracé lève le crayon, et que l'on préfère souvent ne pas lever le crayon pour la tracer. Pour ce faire, nous définissons une autre procédure dragonBis qui dessine la courbe à l'envers. La procédure dragon sera définie récursivement en fonction de dragon et dragonBis. De même, dragonBis est définie récursivement en termes de dragonBis et dragon. On dit alors qu'il y a une récursivité croisée.

static void dragon (int n, int x, int y, int z, int t)  {
  int u, v;

  if (n == 1) {
      moveTo (x, y);
      lineTo (z, t);
  } else {
      u = (x + z + t - y) / 2;
      v = (y + t - z + x) / 2;
      dragon (n-1, x, y, u, v);
      dragonBis (n-1, u, v, z, t);
  }
}

static void dragonBis(int n, int x, int y, int z, int t)  {

  int u, v;

  if (n == 1) {
      moveTo (x, y);
      lineTo (z, t);
  } else {
      u = (x + z - t + y) / 2;
      v = (y + t + z - x) / 2;
      dragon (n-1, x, y, u, v);
      dragonBis (n-1, u, v, z, t);
  }

}

Il y a bien d'autres courbes fractales comme la courbe de Hilbert, courbe de Peano qui recouvre un carré, les fonctions de Mandelbrot. Ces courbes servent en imagerie pour faire des parcours ``aléatoires'' de surfaces, et donnent des fonds esthétiques à certaines images.

2.5 Quicksort

Cette méthode de tri est due à C.A.R Hoare en 1960. Son principe est le suivant. On prend un élément au hasard dans le tableau à trier. Soit v sa valeur. On partitionne le reste du tableau en 2 zones: les éléments plus petits ou égaux à v, et les éléments plus grands ou égaux à v. Si on arrive à mettre en tête du tableau les plus petits que v et en fin du tableau les plus grands, on peut mettre v entre les deux zones à sa place définitive. On peut recommencer récursivement la procédure Quicksort sur chacune des partitions tant qu'elles ne sont pas réduites à un élément. Graphiquement, on choisit v comme l'un des a_i à trier. On partitionne le tableau pour obtenir la position de la figure 2.5 (c). Si g et d sont les bornes à gauche et à droite des indices du tableau à trier, le schéma du programme récursif est

static void qSort(int g, int d)  {

  if (g < d) {
      v = a[g];
      Partitionner le tableau autour de la valeur v
      et mettre v à sa bonne position m
      qSort (g, m-1);
      qSort (m+1, d);
  }
}

Nous avons pris a[g] au hasard, toute autre valeur du tableau a aurait convenu. En fait, la prendre vraiment au hasard ne fait pas de mal, car ça évite les problèmes pour les distributions particulières des valeurs du tableau (par exemple si le tableau est déjà trié). Plus important, il reste à écrire le fragment de programme pour faire la partition. Une méthode ingénieuse [6] consiste à parcourir le tableau de g à d en gérant deux indices i et m tels qu'à tout moment on a a_j < v pour g < j £ m, et a_j ³ v pour m < j < i. Ainsi

Figure 2.5 : Partition de Quicksort

m = g;
for (i = g+1; i <= d; ++i)
    if (a[i] < v) {
        ++m;
        x = a[m]; a[m] = a[i]; a[i] = x; // Echanger a_m et a_i
    }

ce qui donne la procédure suivante de Quicksort

static void qSort(int g, int d)  {

  int i, m, x, v;

  if (g < d) {
      v = a[g];
      m = g;
      for (i = g+1; i <= d; ++i)
          if (a[i] < v) {
              ++m;
              x = a[m]; a[m] = a[i]; a[i] = x; // Echanger a_m et a_i
          }
      x = a[m]; a[m] = a[g]; a[g] = x;         // Echanger a_m et a_g
      qSort (g, m-1);
      qSort (m+1, d);
  }
}

Cette solution n'est pas symétrique. La présentation usuelle de Quicksort consiste à encadrer la position finale de v par deux indices partant de 1 et N et qui convergent vers la position finale de v. En fait, il est très facile de se tromper en écrivant ce programme. C'est pourquoi nous avons suivi la méthode décrite dans le livre de Bentley [6]. Une méthode très efficace et symétrique est celle qui suit, de Sedgewick [47].

static void quickSort(int g, int d) {

  int v,t,i,j;

  if (g < d) {
      v = a[d]; i= g-1; j = d;
      do {
          do 
              ++i; 
          while (a[i] < v);
          do 
              --j; 
          while (a[j] > v);
          t = a[i]; a[i] = a[j]; a[j] = t;
      } while (j > i);
      a[j] = a[i]; a[i] = a[d]; a[d] = t;
      quickSort (g, i-1);
      quickSort (i+1, d);
  }
}

On peut vérifier que cette méthode ne marche que si des sentinelles à gauche et à droite du tableau existent, en mettant un plus petit élément que v à gauche et un plus grand à droite. En fait, une manière de garantir cela est de prendre toujours l'élément de gauche, de droite et du milieu, de mettre ces trois éléments dans l'ordre, en mettant le plus petit des trois en a₁, le plus grand en a_N et prendre le médian comme valeur v à placer dans le tableau a. On peut remarquer aussi comment le programme précédent rend bien symétrique le cas des valeurs égales à v dans le tableau. Le but recherché est d'avoir la partition la plus équilibrée possible. En effet, le calcul du nombre moyen C_N de comparaisons emprunté à [47] donne C₀ = C₁ = 0, et pour N ³ 2,

C_N = N + 1 +

1 £ k £ N

(C_k-1 + C_N-k)

D'où par symétrie

C_N = N + 1 +

1 £ k £ N

C_k-1

En soustrayant, on obtient après simplification

N C_N = (N+1) C_N-1 + 2 N

En divisant par N(N+1)

C_N

N+1

C_N-1

N+1

C₂

3 £ k £ N

k+1

En approximant

C_N

N+1

» 2

1 £ k £ N

» 2

ó
õ

dx = 2

D'où le résultat

C_N » 1,38 N log₂ N

Quicksort est donc très efficace en moyenne. Bien sûr, ce tri peut être en temps O(N²), si les partitions sont toujours dégénérées par exemple pour les suites monotones croissantes ou décroissantes. C'est un algorithme qui a une très petite constante (1,38) devant la fonction logarithmique. Une bonne technique consiste à prendre Quicksort pour de gros tableaux, puis revenir au tri par insertion pour les petits tableaux (£ 8 ou 9 éléments).

Le tri par Quicksort est le prototype de la méthode de programmation Divide and Conquer (en français ``diviser pour régner''). En effet, Quicksort divise le problème en deux (les 2 appels récursifs) et recombine les résultats grâce à la partition initialement faite autour d'un élément pivot. Divide and Conquer sera la méthode chaque fois qu'un problème peut être divisé en morceaux plus petits, et que l'on peut obtenir la solution à partir des résultats calculés sur chacun des morceaux. Cette méthode de programmation est très générale, et reviendra souvent dans le cours. Elle suppose donc souvent plusieurs appels récursifs et permet souvent de passer d'un nombre d'opérations linéaire O(n) à un nombre d'opérations logarithmique O(log n).

2.6 Le tri par fusion

Une autre procédure récursive pour faire le tri est le tri par fusion (ou par interclassement). La méthode provient du tri sur bande magnétique (périphérique autrefois fort utile des ordinateurs). C'est aussi un exemple de la méthode Divide and Conquer. On remarque d'abord qu'il est aisé de faire l'interclassement entre deux suites de nombres triés dans l'ordre croissant. En effet, soient á a₁, a₂, ... a_M ñ et á b₁, b₂, ... b_N ñ ces deux suites. Pour obtenir, la suite interclassée á c₁, c₂, ... c_M+N ñ des a_i et b_j, il suffit de faire le programme suivant. (On suppose que l'on met deux sentinelles a_M+1 = ¥ et b_N+1 = ¥ pour ne pas compliquer la structure du programme.)

int[] a = new int[M+1],
      b = new int[N+1],
      c = new int[M+N];

int i = 0, j = 0;

a[M+1] = b[N+1] = Integer.MAX_VALUE; 

for (int k = 0; k < M+N; ++k)
    if (a[i] <= b[j]) {
         c[k] = a[i]; 
         ++i;
     } else {
         c[k] = b[j]; 
         ++j;
     }

Successivement, c_k devient le minimum de a_i et b_j en décalant l'endroit où l'on se trouve dans la suite a ou b selon le cas choisi. L'interclassement de M et N éléments se fait donc en O(M+N) opérations. Pour faire le tri fusion, en appliquant Divide and Conquer, on trie les deux moitiés de la suite á a₁, a₂, ... a_N ñ à trier, et on interclasse les deux moitiés triées. Il y a toutefois une difficulté car on doit copier dans un tableau annexe les 2 moitiés à trier, puisqu'on ne sait pas faire l'interclassement en place. Si g et d sont les bornes à gauche et à droite des indices du tableau à trier, le tri fusion est donc

static void TriFusion(int g, int d)   {

  int   i, j, k, m;

  if (g < d) {
      m = (g + d) / 2;
      TriFusion (g, m);
      TriFusion (m + 1, d);
      for (i = m; i >= g; --i)
           b[i] = a[i];
      for (j = m+1; j <= d; ++j)
           b[d+m+1-j] = a[j];
      i = g; j = d;
      for (k = g; k <= d; ++k)
          if (b[i] < b[j]) {
              a[k] = b[i]; ++i;
          } else {
              a[k] = b[j]; --j;
          }
  }
}

La recopie pour faire l'interclassement se fait dans un tableau b de même taille que a. Il y a une petite astuce en recopiant une des deux moitiés dans l'ordre inverse, ce qui permet de se passer de sentinelles pour l'interclassement, puisque chaque moitié sert de sentinelle pour l'autre moitié. Le tri par fusion a une très grande vertu. Son nombre d'opérations C_N est tel que C_N = 2 N + 2 C_N/2, et donc C_N = O(N log N). Donc le tri fusion est un tri qui garantit un temps N log N, au prix d'un tableau annexe de N éléments. Ce temps est réalisé quelle que soit la distribution des données, à la différence de QuickSort. Plusieurs problèmes se posent immédiatement: peut on faire mieux? Faut-il utiliser ce tri plutôt que QuickSort?

Nous répondrons plus tard ``non'' à la première question, voir section 1. Quant à la deuxième question, on peut remarquer que si ce tri garantit un bon temps, la constante petite devant N log N de QuickSort fait que ce dernier est souvent meilleur. Aussi, QuickSort utilise moins de mémoire annexe, puisque le tri fusion demande un tableau qui est aussi important que celui à trier. Enfin, on peut remarquer qu'il existe une version itérative du tri par fusion en commençant par trier des sous-suites de longueur 2, puis de longueur 4, 8, 16, ....

2.7 Programmes en Caml

(* Fibonaci, voir page X *)
let rec fib n =
  if n <= 1 then 1
  else fib (n - 1) + fib ( n - 2);;

(* Factorielle, voir page X *)
let rec fact n =
  if n <= 1 then 1
  else n * fact (n - 1);;

(* Triangle de Pascal, voir page X *)
let rec C n p =
 if n = 0 || p = n then 1
 else C (n - 1) (p - 1) + C (n - 1) p;;

(* Fibonaci itératif, voir page X *)
let fib n =
  let u = ref 1 and v = ref 1 in
  for i = 2 to n do
    let u0 = !u and v0 = !v in
    u := u0 + v0;
    v := u0
  done;
  !u;;

(* Le même en style fonctionnel *)
let fib n =
  let rec fib_aux k u v =
    if k > n then u
    else fib_aux (k + 1) (u + v) u in
  fib_aux 2 1 1;;

(* La fonction d'Ackermann, voir page X *)
let rec ack m n =
  if m = 0 then n + 1 else
  if n = 0 then ack (m - 1) 1 else
  ack (m - 1) (ack m (n - 1));;

(* La fonction 91, voir page X *)
let rec f91 n =
  if n > 100 then n - 10
  else f91 (f91 (n + 11));;

(* La fonction de Morris, voir page X *)
let rec g m n =
 if m = 0 then 1
 else g (m - 1) (g m n);;

(* Les tours de Hanoi, voir page X *)
let rec hanoi n i j =
   if n > 0 then begin
     hanoi (n - 1) i (6 - (i + j));
     printf "%d -> %d\n" i j;
     hanoi (n - 1) (6 - (i + j)) j;
   end;;

#open "graphics";;
open_graph "";;

let rec dragon n x y z t =
  if n = 1 then begin
    moveto x y;
    lineto z t
  end else begin
    let u = (x + z + t - y) / 2
    and v = (y + t - z + x) / 2 in
    dragon (n - 1) x y u v;
    dragon (n - 1) z t u v
  end;;

(* La courbe du dragon, voir page X *)
let rec dragon n x y z t =
  if n = 1 then begin
    moveto x y;
    lineto z t
  end else begin
    let u = (x + z + t - y) / 2
    and v = (y + t - z + x) / 2 in
    dragon (n - 1) x y u v;
    dragon_bis (n - 1) u v z t
  end

and dragon_bis n x y z t =
  if n = 1 then begin
    moveto x y;
    lineto z t
  end else begin
    let u = (x + z - t + y) / 2
    and v = (y + t + z - x) / 2 in
    dragon (n - 1) x y u v;
    dragon_bis (n - 1) u v z t
  end;;

clear_graph();;
dragon 15 120 120 50 50;;

(* Quicksort, voir page X *)

let rec qsort g d =
  if g < d then begin
    let v = a.(g)
    and m = ref g in
    for i = g + 1 to d do
      if a.(i) < v then begin
        m := !m + 1;
        let x = a.(!m) in
        a.(!m) <- a.(i); a.(i) <- x
      end
    done;
    let x = a.(!m) in
    a.(!m) <- a.(g); a.(g) <- x;
    qsort g (!m - 1);
    qsort (!m + 1) d
  end;;

(* Quicksort, voir page X *)
let rec quicksort g d =
  if g < d then begin
    let v = a.(d)
    and t = ref 0
    and i = ref (g - 1)
    and j = ref d in
    while j > i do
      incr i;
      while a.(!i) < v do incr i done;
      decr j;
      while a.(!j) > v do decr j done;
      t := a.(!i);
      a.(!i) <- a.(!j);
      a.(!j) <- !t
    done;
    a.(!j) <- a.(!i);
    a.(!i) <- a.(d);
    a.(d) <- !t;
    quicksort g (!i - 1);
    quicksort (!i + 1) d
  end;;

(* Tri fusion, voir page X *)

let b = make_vect n 0;;

let rec tri_fusion g d =
  if g < d then begin
    let m = (g + d) / 2 in
    tri_fusion g m;
    tri_fusion (m + 1) d;
    for i = m downto g do
     b.(i) <- a.(i) done;
    for i = m + 1 to d do
     b.(d + m + 1 - i) <- a.(i) done;
    let i = ref g and j = ref d in
    for k = g to d do
      if b.(!i) < b.(!j) then begin
        a.(k) <- b.(!i); incr i
      end else begin
        a.(k) <- b.(!j); decr j
     end
    done
  end;;

1: Certains systèmes peuvent donner des résultats partiels, par exemple le système SYNTOX de François Bourdoncle qui arrive à traiter le cas de cette fonction