OADymPPaC

Tools for Dynamic Analysis and Debugging of Constraint Programs Outils pour l'Analyse Dynamique et la mise au Point de
Programmes avec Contraintes

Classical Examples: graceful graphs

Problem Description:

A graph with n labelled nodes and q labelled edges is said "graceful" iff each node has different label in [0 .. q] each edge between nodes i j of labels xi xj has label |xi-xj| and all edge labels are differents.
This Problem seems to originate from telecommunications

symetry of values: xi -> q-xi (replacement by the complement)
symetry of variables: cliques, path reversibility

Nota:
simple graphs with trivial solution: q+1 nodes and q edges (star type)
simple graphs with non trivial solution: q+1 nodes and q edges (linear type)

Difficult case: 2 cliques of 5 nodes (K5P2 in [1])

Interest :

Problems with general and specific symetries which depend on the graph.
School problem with difficult instances (one solved in [1])

References :

[1] Karen E. Petrie. Why SBDD can be worse than SBDS. SymCon'03, Kinsale, Ireland, Workshop on Symetries in CSP
[2] Karen E. Petrie, Barbara Smith. Symetry breaking in graceful Graphs. TR APES-56a-2003, http://www.dcs.st-and.ac.uk/~apes/apesreports.html

Sources GNU:

Source with no symetries broken with symmetries broken with sbds .

Data n nodes and q edges:
star: n5q4.pl, line: n8q7.pl, 2 cliques of 3 n6q9.pl, 2 cliques of 4 n8q16.pl, 2 cliques of 5 n10q25.pl,

Codeine Traces:

trace k6p2 (n6q9) allsol, no symetry broken (352525 events ; 2,1M ; unziped 24M)
trace k6p2 (n6q9) allsol, all symetries broken (110771 events ; 2,3M ; unziped 44M) (this trace is more detailed: it gives the variables domains at each node in the search-tree)

this version uses the constraint dist(XI,XJ)#=#DIJ (version gracefulgraph-gnu-sbds.pl) and the maxinteger is 9.

Traces analyze:
The feature of symmetries is straightforwardly linked to the different instances and their study must be made in consequence. The cases of KnP2 problems (2 cliques of n nodes, corresponding to 2xn nodes and q=n*n edges) are an interresting one. The size's trace being big we examine first K3P2 and K4P2.

Symmetries in KNP2 problems:
nd(i) will be the ith node, x(i) the value of the ith node.

complement symmetry: x(i)->q-x(i)
intra-clique symmetry: the set of couple {nd(i),nd(i+n)} can be permuted with any other couple.
inter-clique symmetry: cliques can be swapped.

K3P2 problem (6 nodes, 9 edges):
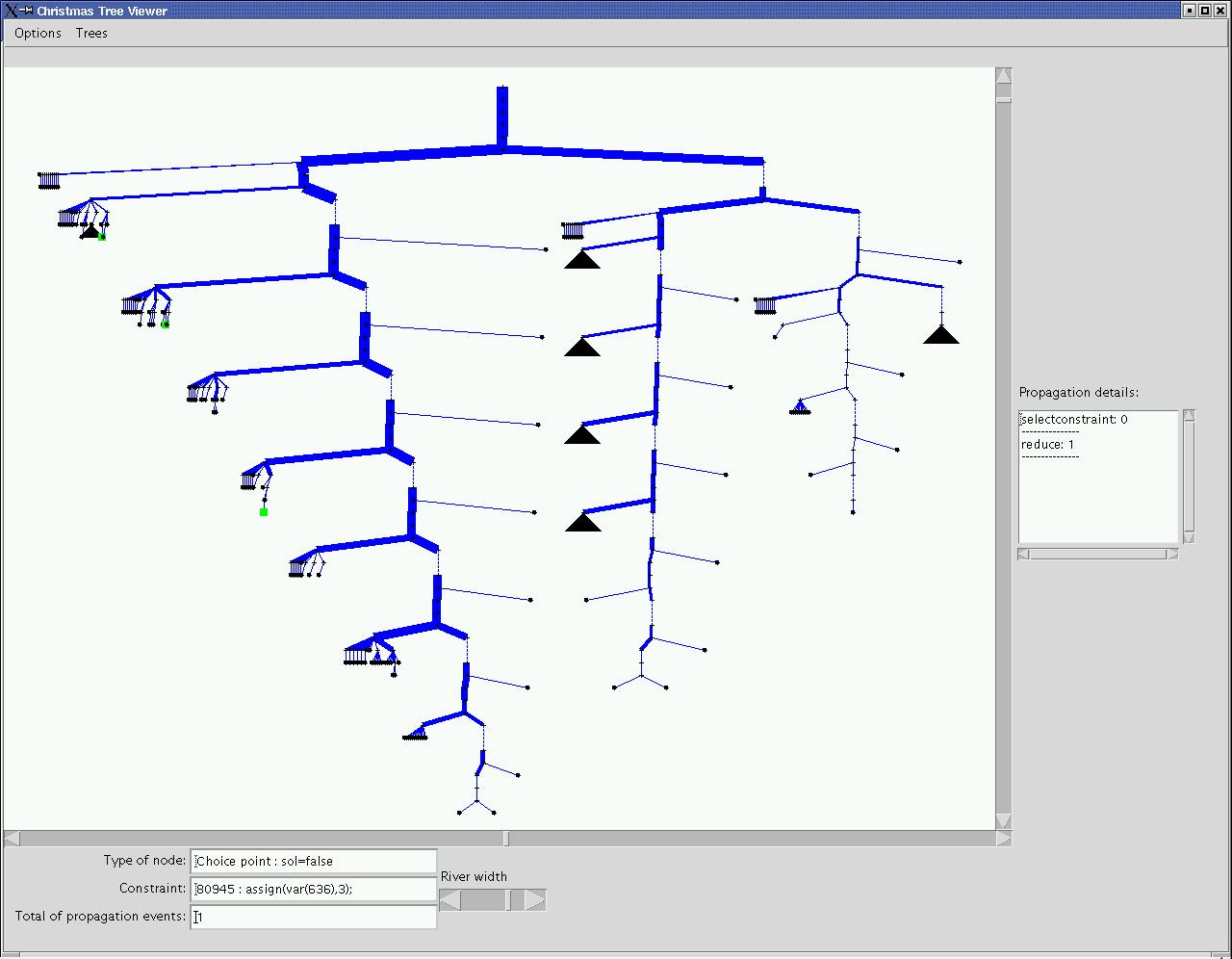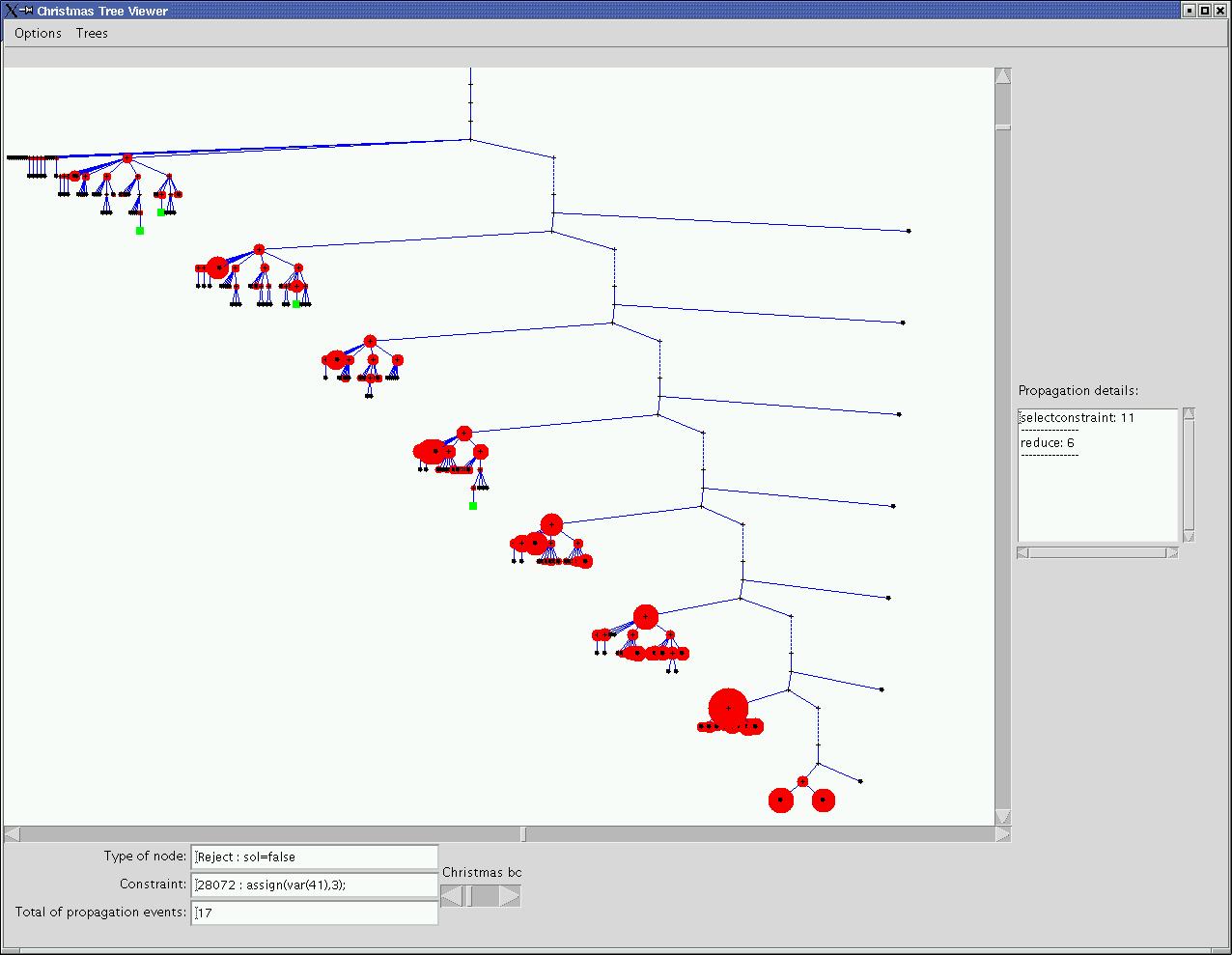In this (corresponding to the a) we can see the propagation tree of the k3p2 problem. The width of the branchs represents the number of propagations to reach the next node of the tree. All symmetries have been broken and only 4 distinct solutions remain (in green in the view). There are two big subtrees in the first choice point, the first with all solutions corresponds to the assignment of the first variable (nd(1)) to 0, the second to the constraint nd(1)&neq;0. We can reasonnably deduce that the problem impose that one variable must be equal to zero. And indeed if all edges are differents and are labeled from 1 to 9, one node must be equal to 0 and another to 9 in order to have the edge labeled 9. Thus nd(1) is imposed to 0 and value 9 is retired from all variables no connected to nd(1) (new trace and ).