


This section is dedicated to optimizations that are first pertinent for the join technique and that are performed by the current version of the join compiler.
We first introduce optimizations that improve the runtime behavior of programs, both in speed and dynamic memory usage. Then, we show how to reduce emitted code size. We focus on optimizing definitions written in object-oriented style, as described in the tutorial [7]. As this programming style proved quite frequent, it is normal for us compiler writers to concentrate our efforts on such definitions.
In this style, a definition is an objet. Object state is encoded by asynchronous state names, while synchronous methods access or modify object state. For instance, given one state name S and n methods m1, m2,…mn taken in that order, we get:
let create(x_0) =
let S(x) | m_1() = P_1(x)
and S(x) | m_2() = P_2(x)
....
and S(x) | m_n() = P_n(x) in
S(x_0) | reply m_1,m_2,...,m_n to create
;;
The synchronous call create(v) creates a new
object (i.e. a new S, m1, m2,…mn definition)
and then sends back a n-tuple of its methods. Moreover, this call
initializes object state with the value v.
As a working example of an object-style definition, consider the following adder:
let create(x_0) = let S(x) | get() = S(x) | reply x to get and S(x) | add(y) = S(x+y) | reply to add in S(x_0) | reply get,add to create ;;
The adder has one state name S and two methods get and add. We
then try to figure out some “normal” runtime behavior for it. As
the initial S(x_0) is forked as soon as the adder definition
has been created, a highly likely initial situation is that there is
one message pending on S and none on the other names. Later on,
as some external agent invokes the get or add method, the message
pending on S is consumed and the appropriate guarded process is
fired. Either process quickly sends a message on S. Thus, a likely
behavior is for the queue of S to alternate between being empty and
holding one element, the queue being empty for short periods. By some
aspects of the compilation of “|” and of our scheduling
policy that we will not examine here, this behavior is almost certain.
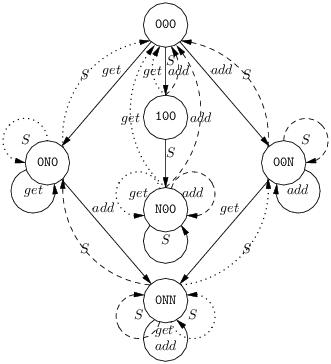
As a matter of fact, this “normal” life cycle involves a blatant waste of memory, queue elements (cons cells) are allocated and deallocated in the general dynamic fashion, while the runtime usage of these cells would allow a more efficient policy. It is more clever not to allocate a cell for the only message pending on S and to use the queue entry attributed to S in the runtime definition as a placeholder. On the status side, this new situation is rendered by a new “1” status. Hence, S now possesses a three valued status: 0 (no message), 1 (one message in the queue slot) or N (some messages organized in a linked list). Thus, assuming for the time being, that there may be an arbitrary number of messages pending on S, the adder compiles into the automaton of figure 2 (adder names are taken in the order S, get, add). This new automaton can be seen as an evolution of the A, B, C automaton of figure 1, with a slight change in channel names.
Using the status 1 not only spares memory, it also avoids some of the runtime tests that compute post-matching status. Basically, when a matching consumes the sole message pending on a name with status 1, then the automaton already knows that this name queue is empty. For instance, when the automaton of figure 2 is in the 100 status and that a message arrive on either one of the two methods, then the appropriate process is fired and status goes back to 000 without any runtime test. By contrast, when the automaton is in the 00N status and that a message arrive on S, the second guarded process is fired immediately, but a test on add queue is then performed: if this queue is now empty then status goes back to 000, otherwise status remains 00N. Receiving a message on S when status is 0NN is a bit more complicated. First, the automaton chooses to consume a message pending on either one of the two methods and to fire the appropriate process (figure 2 does not specify this choice). Then, the queue of the selected method has to be tested, in order to determine post-matching status.
Status 1 is easy to implement using the join compilation technique. The compiler issues different method codes for 100 and N00, and different codes can find S argument at different places. Implementing status 1 in jocaml would be more tricky, since the encoding of states using bit-patterns would be far less straightforward than with 0/N statuses only. As a consequence, the jocaml compiler does not perform the space optimization described in this section.
The automaton of figure 2 has a N00 status, to
reflect the case when there are two messages or more pending on S.
However, one quite easily sees that that status N00 is
useless. First, as S does not escape from the scope of its
definition, message sending on S is performed at three places only:
once initially (by S(x_0)) and once in each guarded process.
Thus, there is one message pending on S initially. A single message
pending on S is consumed by any match and the process fired on that
occasion is the only one to send one message on S. Therefore, there
cannot be two messages or more pending on S. As a consequence the
full automaton can be simplified by suppressing the N00 node
and every edge that starts from it or leads to it.
In particular, there is no more S-labeled edge starting from node 100. In the join implementation this means that the code entry for S needs not be updated when going from status 000 to 100. This entry is simply left as it is. Symmetrically, the code entry for S will not have to be restored when status goes back to 000 after matching.
Another important usage of semantical analysis is determining which names are state names. For a given definition, the output of the analyzer is a status set S, which is a safe approximation of the actual runtime statuses of that definition. State names are the asynchronous names such that all statuses in S give them the status 0 or 1.
The current join compiler includes a rudimentary name usage analyzer, which suffices for object definitions given in the style of the S, m1, m2, …, mn definitions , where all state variables are asynchronous and do not escape from the scope of their definition.
An promising alternative would be to design an ad hoc syntax for distributed objects, or, and this would be more ambitious, a full object-oriented join-calculus. Then, the state variables of object-definitions would be apparent directly from user programs.
Consider any definition that defines n names. Ignoring 1 statuses, the size of the status space of a given definition already is 2n. The size of the non-matching status space is thus bounded by 2n. As a full automaton for this definition has one state per non-matching status, status space size explosion would be a real nuisance in the case of the join compiler. In particular, there are n times the number of non-matching statuses automaton code entries to create.
Unfortunately the exponential upper bound is reached by practical programs, as demonstrated by the general object-oriented definition given at the beginning of this section 5. In that case, all definition statuses such that S has the 0 status are non-matching. In such a situation, using runtime testing, as jocaml does, is not that much a penalty, when compared to code size explosion.
We thus introduce dynamic behavior in the automata. We do so on a name per name basis: the status of state names will be encoded by automata states as before, whereas method statuses will now be explicitly checked at runtime. Thus, we introduce “?”, a new status, which means that nothing is known about the number of messages pending on a name. Additionally, we state that all methods will have the ? status, as soon as there is one message or more pending on any of the methods.
This technique can be seen as merging some states of the full automaton compiled by considering complete status information into new states with ? statuses in them.
For instance, in the adder example, we get the automaton of figure 3, where the three statuses 0N0, 0NN and 00N of figure 2 merge into the new status 0??. (Note that we also take advantage of name usage analysis to delete status N00.)
Information on where runtime testing has to be performed can be inferred from the diagram of figure 3. For instance, assume that current status is 0?? and that a message arrives on S. Since there is at least one message pending on a method, a matching will occur. Tests are needed though, before matching to determine the matching clause, and after matching to determine post-matching status. Abstractly, the first series of tests changes the ? statuses in either 0 or N statuses, while the second series checks if there are still messages pending on names with ? status. We are still investigating on how to organize these tests efficiently without producing too much code (see [2, 10] for a discussion of the size of such code in the context of compiling ML pattern-matching).
By contrast, when status is 100 and that a message arrives on get or add, then the corresponding matching is known immediately and the message pending on S is consumed. Then, the queue for S is known to be empty and status can be restored to 000 with no runtime testing at all. As message arrival order is likely to be first one message on S and then one message on get or add the final automaton of figure 3 responds efficiently to more frequent case, still being able to respond to less frequent cases (for instance, two messages on methods may arrive in a row). Furthermore, when trouble is over, the automaton has status 000 and is thus ready for the normal case. In this example, a penalty in code size is paid for improving code speed in the frequent, “normal” case, whereas this penalty is avoided in non-frequent cases, which are treated by less efficient code.
We introduced a ? status on a name per name basis. However, there are other choices possible: a priori, there are many ways to merge full automata states into final automata states. However, if one really wants to avoid status space explosion the final automaton should be constructed directly, without first constructing the full automaton. Adopting our per name ? status makes this direct construction possible. Additionally, the ? status can be used by the simple static analyzer as a status for the names it cannot trace (e.g. names that escape their definition scope). This dramatically decreases the size of analyzer output and its running time.


